CMOS图像传感器光电二极管模型*

秦 臻,林祖伦*,叶祥平,祁康成,王小菊

(1.电子科技大学光电信息学院,成都 610054;2.广东省惠州市质量计量监督检测所,广东 惠州 516003)



CMOS图像传感器光电二极管模型*

秦 臻1,2,林祖伦1,2*,叶祥平1,2,祁康成1,2,王小菊1,2

(1.电子科技大学光电信息学院,成都 610054;2.广东省惠州市质量计量监督检测所,广东 惠州 516003)

为了更好的对CMOS图像传感器中光电二极管的光电转换物理现象进行研究,需要建立正确合适的光电二极管数学物理模型。通过少数载流子稳态连续方程建立光电二极管的一维物理模型,求解方程后,代入参数在MATLAB中对两层结构的n+/p-sub型和n-well/p-sub型,以及三层结构的p+/n-well/p-sub型二极管进行了计算模拟,得到了3种二极管响应率与波长的关系曲线。最后将结果与实际值进行了对比分析,确认了模型能够在一定程度上反映实际的物理情况。

CMOS;图像传感器;光电流;光电二极管;吸收系数

最近几年,由于CMOS技术和工艺的迅速发展,因而在固态图像传感器领域里,CMOS图像传感器越来越受到重视。而在CMOS传感器中主要运用的光电转换结构是光电二极管,其性能对整个成像系统的性能有着很重要的作用。所以对于传感器的研究首先要了解光电二极管的光谱响应特性,因此有必要建立合适的光电二极管模型。由于整个图像传感器系统要集成到同一块芯片上面,因此光电二极管的结构必须要遵循标准CMOS工艺能够生产的PN结,而不能另外增加制造工艺。本文参考了众多文献中对光电二极管建模[1-5]以及分析[6-7]的方法,主要在文献[8]中的基本建模方法之上,通过少数载流子的稳态连续方程来建立光电二极管的一维数学物理模型。最后通过求解方程和仿真计算,得到3种结构光电二极管响应率与波长之间的关系。

1 建立CMOS光电二极管模型

1.1 物理结构

根据标准n-well CMOS工艺,光电二极管的物理结构主要有3种,包括两层结构的n+/p-sub和n-well/p-sub,以及三层结构的p+/n-well/p-sub。图1和图2分别为两层和三层结构示意图,图中标注了各层的厚度。

1.2 半导体材料光吸收

半导体材料中,入射光的光通量φ(x)随入射深度增加呈现指数衰减。可以表示为:

φ(x)=φ(0)×exp(-α(λ)x)

(1)

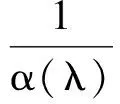
(2)

图1 两层结构(n+/p-sub或n-well/p-sub)

图2 三层结构(p+/n-well/p-sub)

波长与吸收长度的关系如图3所示。

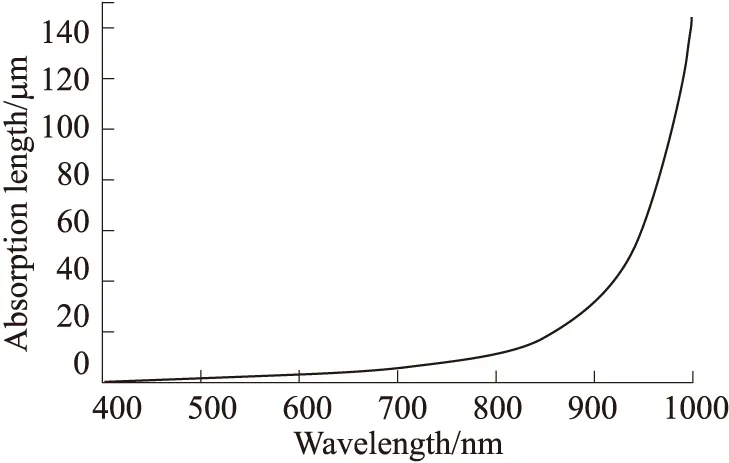
图3 波长与吸收长度的关系

式(1)中的φ(0)表示为:

(3)

其中:Pin为单位面积上的光功率,R为界面处对光的反射系数,h为普朗克常量,v为入射光频率。

1.3 建立两层结构模型

按照图1所示的两层结构,可以将其分为3个区域:P区、空间电荷区和N区,这3个区域都能产生光电流。P区和N区的电流是通过少数载流子扩散产生的。空间电荷区的电流是通过其中的电子空穴对在内建电场作用下的漂移运动产生。接下来将计算3个区域的电流密度。

(1)N区电流密度

按照非平衡载流子扩散漂移运动规律,N区中由光照产生的空穴为少数载流子,主要通过做扩散运动来产生电流。根据扩散定律,得到该区域中空穴对应的稳态连续性方程:

(4)

其中:Dp是空穴扩散系数,τp是空穴寿命,pn0是光照前平衡状态下的空穴浓度,pn(x)是受光照后非平衡情况下总的空穴浓度。方程第1项表示单位体积时间内累积的电子空穴对数量,第2项表示单位体积时间内复合掉的电子空穴对数量。G(λ,x)是光生电子空穴对产生率,有:

(5)

在恒定光照条件下,达到平衡,即单位体积时间内产生的电子空穴对和复合掉的电子空穴对数量相等,得到式(4)。

对于光照表面x=0处,有边界条件:

(6)

其中:Sp是半导体表面的空穴复合速率。

对于N区与空间电荷区的边界x=x1处,有边界条件:

(7)

这里的Vbias是二极管所加反向偏置电压的大小,前面的负号指出是反向电压,k是波尔兹曼常数,T是温度。

式(4)本身有解析的通解,在这里利用两个边界条件式(6)和式(7),再代入式(5)可以直接求得方程(4)的特解。得到的空穴浓度函数pn(x)可以通过式(8)得到N区的电流密度:

(8)

其中,q是电荷量。

(2)P区电流密度

对于P区,同样的,有少数载流子电子的稳态连续性方程:

(9)

同样,P区x=x3处边界条件:

(10)

P区与空间电荷区边界x=x2处,有边界条件:

(11)

同样可以求得P区电流密度:

(12)

(3)空间电荷区电流密度

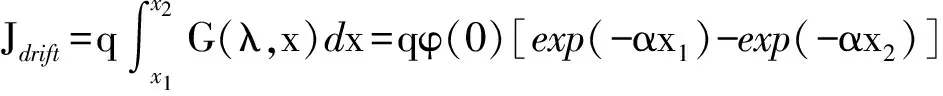
(13)

(4)总光电流密度

以上所有求出的电流密度都包含了暗电流,暗电流是主要由二极管上的反偏电压导致的,令G(λ,x)为零可以求得总的暗电流密度Jdark,从总的电流密度中减去Jdark就可以得到总的光电流密度:

Jopt=JN+Jdrift+JP-Jdark

(14)

1.4 建立三层结构模型

图2是三层结构示意图,分为5个区域。P1、P2区和N区电流密度计算方法与两层结构相同,只是边界条件略有不同。空间电荷1、2区的电流密度计算方法也与前面相同,但是需要变更积分边界条件。

同样可以得到三层结构光电二极管的总光电流:

Jopt=JP1+JN+JP2+Jdrift1+Jdrift2-Jdark

(15)

2 模拟结果与分析对比

半导体参杂浓度和各层厚度由所使用的CMOS工艺决定。代入合适的参数后在MATLAB中进行仿真模拟。

图4是n-well/p-sub型二级管响应率的仿真结果与实际硅光电二级管厂商资料数据的对比。可以看到仿真结果与实际值在大体上相符,但是在偏短波区域和偏长波区域,仿真结果相对于实际数据最高有60%左右的偏低(短波长区域约0.07A/W左右,长波长区域约0.2A/W左右)。存在的不一致应该是仿真计算时所使用的半导体工艺参数与实际产品的差别所造成的。

图5是建立的3种不同结构的光电二极管模型的响应率曲线对比。可以看到在长波长区域3种结构的二极管响应率区别不大,在短波长区域,n+/p-sub型二极管的响应率要比n-well/p-sub型的高。而三层结构的p+/n-well/p-sub型二极管,其整体响应率都要大大高于两种两层结构的二极管。

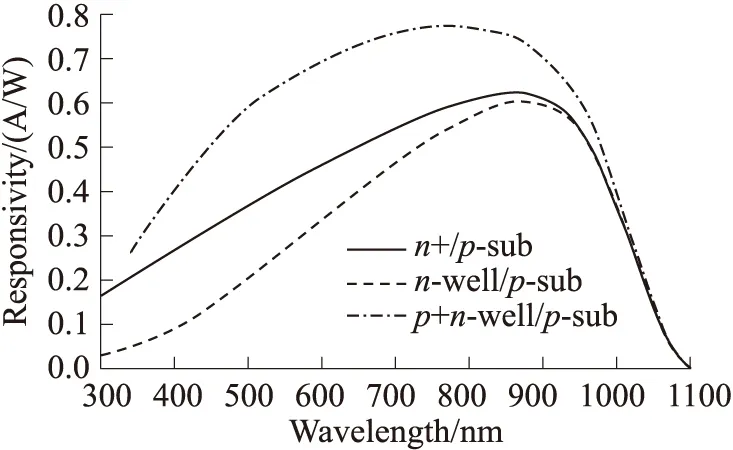
图5 不同结构光电二极管的响应率对比

由图3半导体材料对光的吸收特性曲线,波长越短的光在材料中衰减的越快,因此短波长的光很难到达光电二极管较深的区域。而n-well/p-sub型光电二极管的空间电荷区比n+/p-sub型的深,因此导致其对短波长的响应率在最差的位置要比后者差接近80%(约0.13 A/W)。三层结构的二极管有最好的响应率,是因为它拥有两个空间电荷区,提高了光子的收集效率。但是,p+/n-well/p-sub型二极管的两个空间电荷区同样增加了它的结电容,从而导致更低的转换增益和灵敏度,所以其更高的响应率并无优势。

3 结论

本文详细的介绍了通过连续稳态方程建立光电二极管一维数学物理模型的过程,并以此为基础在MATLAB上对n+/p-sub、n-well/p-sub以及p+/n-well/p-sub 3种结构的光电二极管进行了仿真计算。仿真结果与实际数据有较好的相符,表明了所建立的模型的正确性。最后从理论上分析对比了3种结构光电二极管的光响应率特性。希望该模型的建立工作能为后续的改进和光电二极管的分析提供有用的帮助。

[1]Huiming Z,Tingcun W,Ran Z. Modeling of Pinned Photodiode for CMOS Image Sensor[C]//Signal Processing,Communications and Computing(ICSPCC),2011 IEEE International Conference on. IEEE,2011:1-4.

[2]刁静. 有源像素CMOS图像传感器的设计研究[D]. 电子科技大学,2006.

[3]颜永红,汪立. 一维0. 18 μm CMOS光电二极管量子效率的研究与模拟[J]. 电子器件,2008,31(4):1073-1076.

[4]Lee J S,Hornsey R I,Renshaw D. Analysis of CMOS Photodiodes. i. Quantum Efficiency[J]. Electron Devices,IEEE Transactions on,2003,50(5):1233-1238.

[5]刁静,林祖伦. 用于CMOS图像传感器的光电二极管的模型[J]. 传感技术学报,2006,19(03):702-708.

[6]Leblebici Y,Etienne-Cummings R,Koklu G,et al. Characterization of Standard CMOS Compatible Photodiodes and Pixels for Lab-on-Chip Devices[C]//Proceedings of the 2013 IEEE International Symposium on Circuits and Systems(ISCAS). 2013(EPFL-CONF-187943):1075-1078.

[7]Koklu G,Etienne-Cummings R,Leblebici Y,et al. Characterization of Standard CMOS Compatible Photodiodes and Pixels for Lab-on-Chip Devices[C]//Circuits and Systems(ISCAS),2013 IEEE International Symposium on. IEEE,2013:1075-1078.

[8]Liu W J,Chen O T C,Dai L K,et al. A CMOS Photodiode Model[C]//Behavioral Modeling and Simulation,2001. BMAS 2001. Proceedings of the Fifth IEEE International Workshop on. IEEE,2001:102-105.

秦臻(1988-),男,汉族,四川成都人电子科技大学硕士研究生,主要研究方向为CMOS图像传感器,qzqinzhen@gmail.com;

林祖伦(1950-),男,汉族,四川人,电子科技大学光电信息学院教授,研究生导师,主要研究方向为真空电子技术与新型显示技术,zllin@uestc.edu.cn。

ModelingofPhotodiodeforCMOSImageSensor*

QINZhen1,2,LINZulun1,2*,YEXiangping1,2,QIKangcheng1,2,WANGXiaoju1,2

(1.School of Opto-Electronic Information,University of Electric Science and Technology of China,Chengdu 610054,China;2.Guangdong Huizhou Quality and Measuring Supervision Testing Institute,Huizhou Guangdong 516003,China)

In order to research on the photoelectric conversion phenomena of photodiode for CMOS image sensor,we construct an accurate and reasonable mathematical-physical model. We utilize the minority carrier equilibrium continuity equations to establish an one-dimensional physical model of photodiode. By means of MATLAB,the relationship between responsivity and wavelength of photodiode(including three types:two-layer structure ofn+/p-sub type andn-well/p-sub type,and three-layer structure ofp+/n-well/p-sub type)is found out. Finally,the simulation results are analyzed and compared with practical data. We confirmed the model can basically reflect the actual physical situation.

CMOS;image sensor;photocurrent;photodiode;absorption coefficient

项目来源:中央高校基本科研业务项目(ZYGX2010J062);电子科大-四川长虹“信息显示器件联合实验室”项目

2013-09-27修改日期:2013-11-04

10.3969/j.issn.1005-9490.2014.06.006

:TP212.1;TN364.2

:A

:1005-9490(2014)06-1039-04