基于结构光方法的类镜面物体的面形测量*
2014-09-06刘建涛蔡佳佳
李 锋,刘建涛,蔡佳佳
(江苏科技大学电子信息学院,江苏 镇江 212003)
基于结构光方法的类镜面物体的面形测量*
李锋*,刘建涛,蔡佳佳
(江苏科技大学电子信息学院,江苏 镇江 212003)
摘要:为了完成对类镜面物体的面形测量,首先分析了光学三维面形测量对物体含有高亮区的反光崎岖表面无法完整测量的原因,然后从测量系统的照明方式出发,提出一种基于结构光的测量的方法。该结构光采用正弦光栅。在双频傅里叶变换轮廓术的基础上,通过起偏器和检偏器的作用,消除了高光表面反射对摄影系统的影响。该方法可以重建类镜面物体,测量精度较原来提高了3倍。理论分析和模拟结果均证明提出的测量方法的可行性和有效性。
关键词:成像光学;结构光;偏振片;双频傅里叶变换
基于结构光的三维面形测量[1]技术以其高精度、高效率和非接触性等优点目前已成为三维测量方法中的主流技术。在一般情况下,测量针对的是表面为漫反射高度变化范围不大的物体[2],但在实际应用中,我们经常会遇到形状复杂表面高光的物体。这种情况下,想要在CCD摄像机中采集到清晰的图像,并且得到很好的测量结果,应该采取不同的照明方式不同的解相方法。对于反光的崎岖表面,镜面反射会带来的相机曝光饱和造成信息的丢失。同时,复杂的高度变化会导致拍摄中产生阴影、断层,给相位展开带来很大的困难,甚至无法进行相位展开。在现代工程应用中,存在大量的类镜面物体需要测量[3]。传统的对类镜面物体表面的测量方法[4]主要有2种:传统的坐标测量仪、改变镜面物体表面的反射特性。这2种方法对物体的材料有很大的限制,也可能改变了测量目标的特性。为了满足需求,众多学者针对类镜面物体[5]也做了很多的研究。文献[6]提出了一种图像高光消除技术,能在一定程度上有效地消除类镜面物体表面上的高光,但是它需要对每张图片进行处理,无法满足实时性要求的测量。文献[7]提出一种将多光源法与补色法相结合的高光分离方法,但该方法易受自然场景干扰,且速度和精度有一定的限制。Zhang S[8]在单目测量系统的基础上提出了一种三步相移算法的高动态范围扫描技术,但该方法很难获得完整的高光表面,且无法满足实时性要求。为了解决这一问题,本文提出一种结构光照明系统,将偏振消光的测量方法应用于双频光栅傅里叶变换测量系统中。将两组不同频率的光栅结合投射到物体表面,先通过偏振消光系统将类镜面的高光消除,然后在相位展开过程中,先展开低频截断相位,然后以低频相位为参考,根据双频光栅2个频率之间的关系,展开高频截断相位,从而得到高精度的恢复面形。
1 偏振消光双频傅里叶变换原理
1.1理论分析
一般地,从一个观察系统获取的二维图像中确定距离维(第3维)信息时,人们必须依赖于物体形态、光照条件等先验知识。然而,采用结构光照明方式,由于三维面形对结构光场的空间或时间调制,可以从携带有三维面形信息的观察光场中解调得出三维面形数据。由于这种方法具有较高的测量精度,作为一种三维面貌计量手段已经得到广泛的应用。对于类镜面物体而言,由于镜面反射的存在,将会导致图像中存在许多的高亮区。因为这些高亮区的光强相对较强,因此图像中高亮区镜面反射光会不可避免地掩盖漫反射光场分布中的相位信息,从而导致无法完成三维面形测量。从分析傅里叶变换轮廓术中光场的偏振特性出发,利用光学器件的滤光作用,结合傅里叶变换轮廓术和光照模型[9],消除高光物体镜面反射光的影响,恢复到普通的漫反射物体表面,实现了含镜面反射的物体面形的三维测量。在对其进行相位展开的过程中,由于物体表面的缺陷,会导致相位信息的丢失而影响相位的展开。所以,采用何种方法进行相位展开直接影响测量结果的精度。因此本文提出一种双频傅里叶变换法检测类镜面物体的方法,更有效的提高测量精度和测量范围。
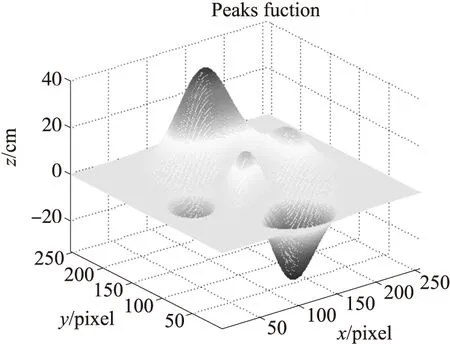
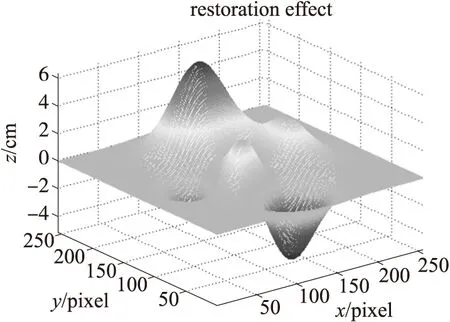
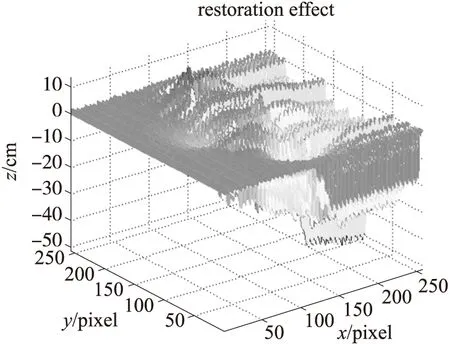
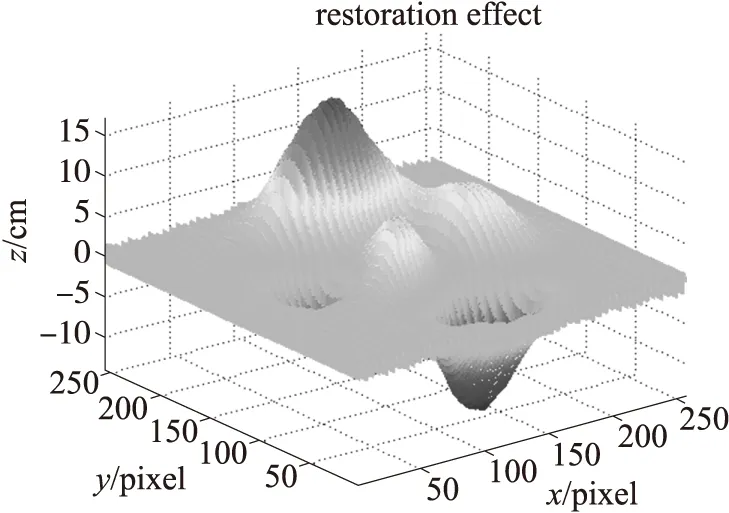
由于选取双频傅里叶变换轮廓术作为测量方法,首先产生频率分别为f1和f2的双频光栅(f1 g1(x,y)=a(x,y)+b1(x,y)cos[(2πf1x+φ1(x,y)]+ b2(x,y)cos[(2πf2x+φ2(x,y)] (1) 其中a(x,y)是背景光强,b1(x,y),b2(x,y)是不同频率分量的对比度,φ1(x,y),φ2(x,y)分别是经物体高度对频率f1和f2调制的调制相位。当被测物含有高亮区的镜面反射时,由光照模型可知,反射光场包含光源的漫反射分量和镜面反射分量。光是一种电磁波,大部分情况下,只需考虑电场分量[10]。当入射光为平行光时,各路镜面反射光仍为平行光,合成后电矢量平行于入射面,这种光表征物体的光泽,即所谓的高光。经物体表面反射后的光强可写成漫反射物体时表面反射光强与镜面反射物体表面反射光强之和,可表示为 g1(x,y)=a(x,y)+b1(x,y)cos[(2πf1x+ φ1(x,y)]+b2(x,y)cos[(2πf2x+φ2(x,y)]+ c1(x,y)cos(2πf1x)+c2(x,y)cos(2πf2x) (2) 式(2)中a(x,y)是代表环境自然光反射分量振幅,b1(x,y)cos[(2πf1x+φ(x,y)],b2(x,y)cos[(2πf2x+φ(x,y)]分别表示对不同频率投影光源的漫反射分量振幅,c1(x,y)cos(2πf1x),c2(x,y)cos(2πf2x)分别表示对不同频率投影光源的镜面反射分量振幅,且该镜面反射分量与CCD拍摄的方向有关,只在某些区域有值,其他区域为零。物体的高度信息包含在漫反射项中的相位φ(x,y)中。 由反射机理可知: c(x,y)≫b(x,y) (3) c(x,y)≫a(x,y) (4) 因此在c(x,y)不为零的区域,镜面反射占主导地位,将这些区域称为高亮区。由上式可见,在高亮区镜面反射掩盖了漫反射项,无法分辨出漫反射项,从而无法正确分辨出包含在漫反射项中的物体相位信息。由于物体面形变化导致的漫反射光,各路漫反射光线由于各点的法线方向不一致,造成反射光线向不同的方向无规则地反射,不再是平行光,因此各路漫反射光相对于镜面反射光的入射面既有平行的电矢量分量又有垂直的电矢量分量。由于物体的高度信息包含在漫反射项中的相位φ(x,y)中[11],由以上分析可知,只要将光源的平行于入射面的平行电矢量分量消除,保留漫反射的垂直于入射平面的电矢量分量,就能求出含镜面反射物体的正确相位信息。 1.2测量原理 图1 偏振消光双频傅里叶轮廓术原理图 由于类镜面物体表面的镜面反射光的影响,本文在原有的测量基础上对测量系统进行了改进,结构光源采用双频的正弦光栅[12],由投影仪投影到物体表面。在投影仪的出瞳前和摄像机的入瞳前分别加上起偏器和检偏器。具体的原理图如图1所示。 其中P1、P2分别为起偏器和检偏器,用于得到满足要求的线偏振光。Ep′、Ep分别是投影系统的入瞳和出瞳,Ec′是成像系统的入瞳,两光轴相交于参考平面R上的O点。d是Ep和Ec′间的距离,L0是Ec′到参考平面R间的距离,h是物面上点D到参考面的距离,A、C是参考平面上的点,B、B′分别是放上被测物体后CCD拍摄光轴与参考平面的交点,D是物面上的点,CCD是接收光栅像的面阵探测器。投影仪投射出频率分别为f1和f2的正弦分布的平行自然光经过起偏器P1后成为电矢量E平行于入射面的线偏振光,即 gp1(x,y)=ap(x,y)+bp1(x,y)cos[(2πf1x+ φ1(x,y)]+cp1(x,y)cos(2πf1x) (5) 由于消光过程中不受频率的影响,所以将式(2)中频率f2省去。将式(2)中的光强分别写成平行于入射面的电矢量分量bp1(x,y)与垂直于入射面的电矢量分量bs1(x,y)的和,则式(5)中gp1(x,y)表示g(x,y)通过起偏器P1后的光强,P1滤掉垂直于入射面的的电矢量分量bs1(x,y)cos(2πf1x+φ1)。此时只剩下平行于入射面的电矢量分量bp1(x,y)cos(2πf1x+φ1),垂直于入射面的电矢量分量不能通过检偏器P2。gp1(x,y)经含镜面反射的物体反射后中的镜面反射电矢量分量平行于入射面,其中的漫反射电矢量分量也平行于入射面,但是由于漫反射因物体的高度分布而导致各个入射面不相互平行,因此各路漫反射电矢量分量合成后为非完全线偏振光。此时垂直于入射面的电矢量为0。旋转P2,当P2与P1相互垂直时,此时反射光中只有垂直于入射面的光矢量分量能通过检偏器P2,则经CCD接收的变形光栅像表达式可写为: gCCD=as(x,y)+bs1(x,y)cos[2πf1x+φ1(x,y)]+ bs2(x,y)cos[2πf2x+φ2(x,y) (6) 由式(6)可知,由于P2阻止了平行于入射面的电矢量分量通过,因此起偏器和检偏器的引入消除了物体表面高亮区产生的镜面反射光,虽然通过消光后环境光分量与漫反射分量振幅系数同时也发生了变化,但是与高度分布密切相关的相位信息并没有改变。此时光场分布形式恢复到只存在漫反射光的状态。因此,镜面反射的影响被消除后按照漫反射方法对其进行处理。先将上式写成指数形式,在低频f1的基础上对其进行傅里叶变换,利用带通滤波器对其进行频域滤波[13],得到基频信息,然后对其进行逆傅里叶变换并求反正切便可得相位φ1(x,y)。从低频截断相位图中确定出截断级次n1,然后在n1的基础上,选择合适的f1和f2,根据f1和f2之间的关系采用以上相同的步骤就可以计算出高频截断相位φ2(x,y)。然后进行相位展开便能得到物体表面的三维信息。f1和f2的选取必须避免携带有用信息的2个频谱之间的混叠以及他们同零级频谱之间发生混叠,还要防止由于抽样不当造成的频谱周期之间的混叠。这样就可以完成高频截断相位图的相位展开。 为了进一步验证方法的有效性,采用计算机模拟对其进行验证。模拟系统的结构参数为d/l=2/5。低频频率f1和高频频率f2分别为1/16和1/4。总的模拟点数为256pixel×256pixel,背景光强和条纹对比度同时设为1。在消除镜面反射光的前提下模拟出双频光栅投影在参考平面上的双频条纹图如图2和一个256×256大小的peaks函数图如图3。 图2 参考正弦双频光栅条纹 图3 peaks函数模拟图 首先对标准的双频光栅采用傅里叶变换轮廓术,得到参考面的连续相位。将peaks函数加入到标准的双频光栅中,可以得到标准双频光栅经过peaks函数调制的变形条纹图如图4所示。对变形的条纹图在频率f1的基础上首先进行傅里叶变化,然后采用带通滤波窗口滤出基频分量,再计算其逆傅里叶变化,然后经反三角运算求得相位级次n1,在n1的基础上,对频率f2做同样的处理求得相位级次信息。用此相位减去标准参考面的相位就会得到由物体调制的相位。利用相位和高度的关系就可以恢复物体的三维面形。图5为单独从高频条纹中获取的peaks函数图,图6为单独从低频条纹中获得的,图7为从双频傅里叶变换中恢复的peaks函数图。 图7 从双频信息中恢复的peaks函数 图4 经过peaks函数调制的变形光栅 图5 单独从高频信息中恢复效果图 图6 单独从低频信息中恢复效果图 由恢复出来的peaks函数可以看出,这种偏振消光的双频傅里叶变换轮廓术法可以得到原物体的基本形貌。通过比较可以看出,从低频条纹中也可以恢复物体形貌,但是只能得到一个模糊的形状,没有很高的精度。单独从高频条纹中,由于相位的截断无法恢复物体的形貌。然而将二者结合起来,高频在低频的基础上进行相位展开就能得到比较精确的物体形貌。对3种方法重建的形貌进行局部分析比较,采用均方差来表示误差,单独从低频光栅恢复的误差为 0.69 mm,然而从双频光栅恢复的误差降到0.25 mm,采用双频光栅投影可以将原来的测量精度提高约为3倍。 相对于传统的三维测量方法,本文提出了基于结构光的测量方法,直接从受物体调制的结构光中提取信息,减少了外界环境光的影响和图像匹配带来的大量的运算,可以实现实时快速的检测。偏振消光双频傅里叶变换轮廓术利用光学器件的光学特性,对现代工业中大量的表面高光崎岖的物体[14]提供了一种很好的检测方法。从实验结果可以看出,对该方法能很好的恢复物体的面形。它不仅克服了镜面反射对图像采集的影响,同时对表面不连续的物体能够对其进行相位展开,并且提高了它的测量精度,从而满足工业检测的需要。 参考文献: [1]Zhang S.Recent Progresses on Real-Time 3D Shape Measurement Using Digital Fringe Projection Techniques[J].Optics and Lasers in Engineering,2010,48(2):149-158. [2]李冠楠,李强.一种基于人脸核心特征的PCA人脸识别算法及应用[J].电子器件,2012,35(5):608-610. [3]陶涛,郭红卫,何海涛.镜面反射面形光学三维测量技术综述[J].光学仪器,2005,7(2):90-95. [4]Yoshinori Y,Hiroyuki M,Osamu N,et al.Shape Measurement of Glossy Objects by Range Finder with Polarization Optical System[J].Gazo Den shi Gakkai Kenkyukai Koen Yoko 200,2003,43-50. [5]Hu Q,Harding K G,Du X,et al.Shiny Parts Measurement Using Color Separation[C]//Proc SPIE 6000,6000D1-8(2005). [6]王中任,全燕鸣.一种金属零件图像高光消除技术[J].机械与电子,2008(10):7-9. [7]姚莉.针对高光表面物体的三维形状获取技术的研究[M].上海:上海交通大学,2007. [8]Zhang S,Yau S T.High Dynamic Range Scanning Technique[C]//Proceedings of the SPIE,vol.7066.San Diego,CA;2009,0336041-0336047. [9]吴亮,周东翔,梁华.一种基于Phong物体光照模型的阴影检测算法[J].现代电子技术,2008(5):124-127. [10]陈其夆,许汉忠,林筱芳.具非对称非球面镜之指纹辨识器的光学设计[J].电子器件,2008,31(1):329-333. [11]Zhang S,Huang P.Novel Method for Structured Light System Calibration[J].Optical Engineering,2006,45(8):083601. [12]胡毅,费业泰,叶斯然.计量光栅空间位姿参数光场输出模型与仿真[J].光电工程,2011(6):71-77. [13]吴国旺,陈晨,徐帆.一种基于自适应均值平滑算法的三维重绘技术[J].传感技术学报,2013,26(4):530-535. [14]Kokku R,Brooksby G.Improving 3D Surface Measurement Accuracy on Metallic Surfaces[C]//Proc SPIE 5856,2005:618-624. 李锋(1970-),男,汉族,陕西省商洛人,副教授,博士,硕士生导师,研究方向为光电信息处理,lifengsl@126.com。 ShapeMeasuringofMirrorObjectBasedonStructuredLightMethod* LIFeng*,LIUJiantao,CAIJiajia (College of Electronics and Information,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China) Abstract:In order to complete the measurement of mirror object,the paper first analyzes the reason that the measurement of 3D surface shape can’t completely measure the object containing reflective rough surface of the highlighted area.Then,starting from the lighting pattern of measurement system,a method of measurement has been proposed based on structure light which uses double-frequency sinusoidal grating.Taking advantage of the polarizer’s and analyzer’s role respectively on the basis of it can eliminate the effect of highlights of the specular reflection on the camera system.The method can rebuild the mirror object and the measurement accuracy is raised three times.Theoretical analysis and experimental results prove the feasibility and effectiveness,of the proposed measurement method. Key words:imaging optics;structure light;polaroid;double-frequency fourier transform doi:EEACC:6140C;7320P10.3969/j.issn.1005-9490.2014.05.018 中图分类号:O439 文献标识码:A 文章编号:1005-9490(2014)05-0882-05 收稿日期:2013-09-16修改日期:2013-11-01 项目来源:国家自然科学基金项目(11204109)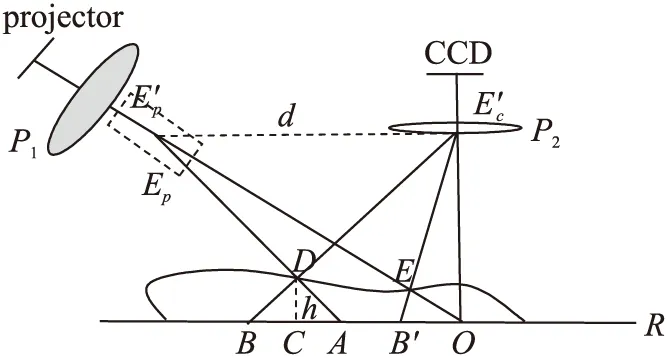
2 计算机模拟结果


3 结论

