高速铁路枢纽衔接服务水平评价体系

李金梅，聂 磊，郭根材，佟 璐

（北京交通大学 交通运输学院，北京 100044）

1 问题描述

我国铁路网点多线长，列车停站多，部分中长距离出行旅客必须选择换乘出行。而换乘客流带来的列车衔接问题以优化枢纽节点的列车衔接方案为重，其深受枢纽衔接服务水平的影响。国内外学者以列车开行方案和运行图为基础，构建列车衔接方案。针对路网换乘优化做了较多的研究，而对于枢纽衔接服务水平评价的研究很少。Spring C. Hsu[1]和 P. Vansteenwegen 等[2]从换乘等待时间方面优化交通路网；张铭等[3]从路网运输能力均衡配置角度，构建轨道交通路网运营协调性影响因素的递阶层次结构模型；Sabyasachee Mishra 等[4]根据图论提出综合运输网络体系衔接性能指标；郭瑾[5]建立了客运枢纽换乘条件评价指标和计算模型；韩宝明等[6]通过客运专线换乘枢纽交通设计评价，为换乘枢纽站内部交通规划设计提供辅助工具。

高速铁路衔接方案优化的目标是实现铁路和旅客需求的动态平衡，换乘的便捷性和舒适性成为影响换乘出行的重要因素。通过建立枢纽衔接服务水平评价体系，从实际运用角度评价枢纽服务水平，能够为衔接方案提供更多辅助信息。

2 枢纽衔接服务水平影响因素评价指标

从枢纽自身条件、列车开行特性和旅客出行效用3个方面分析枢纽衔接服务水平影响因素。枢纽自身条件包括枢纽在路网中的重要性、枢纽连通性和枢纽内换乘站设施协调能力；列车开行特性包括平均运行速度、枢纽列车衔接率、平均运行距离和线路能力等；旅客出行效用体现在换乘客流量、换乘次数和换乘时间方面。为此，构建的枢纽衔接服务水平影响因素评价指标体系如图1所示。

2.1 枢纽自身条件评价指标

枢纽自身条件评价指标建立在其硬件设施为换乘旅客提供的方便性和服务旅客范围度上，具体包括枢纽所处的路网位置重要性、枢纽连通性、枢纽内部协调换乘能力等。

2.1.1 枢纽路网重要性

高速铁路枢纽作为综合运输体系的关节，是客流集散和组织的重要场所，承担着旅客进出站、上下车、中转换乘等作业。枢纽路网重要性与枢纽所在地区人口活动密度、城市经济发展水平、地理位置等因素密切相关，通过设定一个均值参数来衡量枢纽的路网重要性。

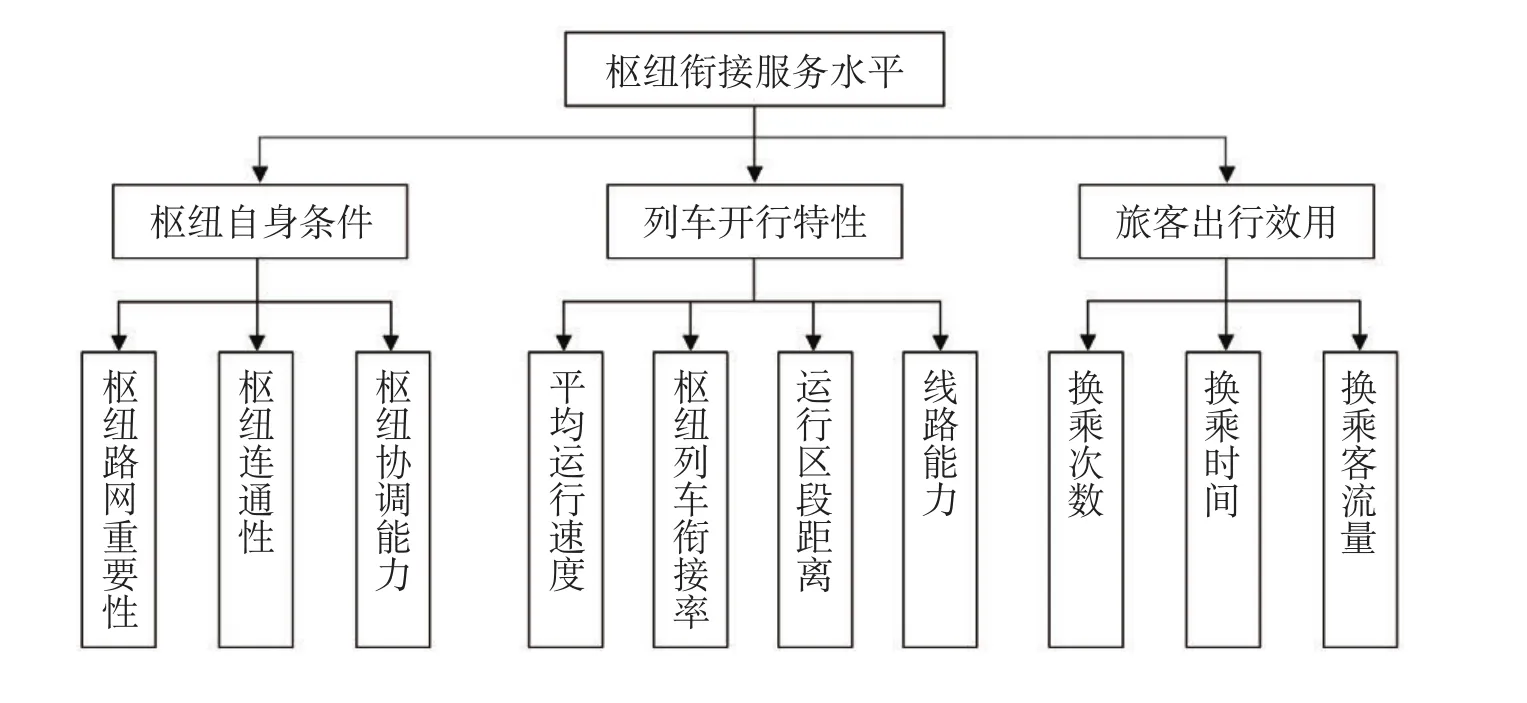
图1 枢纽衔接服务水平影响因素评价指标

式中：xi为路网重要性的影响因素；n 值取3；x1为城市活动密度，体现城市的经济发展模式；H 为区域住户数；E 为城市就业人数；S 为区域土地面积；x2为城市经济发展水平，按照枢纽所在城市的经济水平 GDP 分为4类取值，亿元；x3为枢纽地理位置，根据枢纽距离市中心的距离 l 分为4类取值，km。

2.1.2 枢纽连通性

枢纽连通性表现为枢纽衔接方向、衔接线路和服务范围，其评价指标定义为枢纽内各车站节点连通线路的“衔接权重值[4]”之和。线路衔接权重值与节点衔接方向、线路能力、列车开行特性(平均开行速度、开行距离和发车间隔)有关。定义线路衔接权重值 pj为

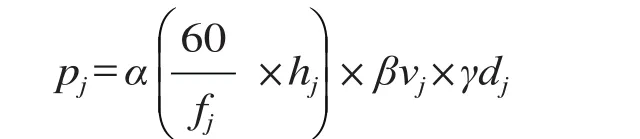
式中：fj为线路列车平均开行频率，列/min；hj为日运营时间，h；vj为线路列车平均运行速度，km/h；dj为线路平均运行距离，km；α、β、γ 分别为线路能力、列车平均运行速度和线路平均运行距离的换算系数，α =1/(枢纽线路平均能力 × 枢纽线路平均开行对数)，β =1/ 枢纽线路平均开行速度，γ =1/枢纽列车平均开行距离。

枢纽连通性指标为

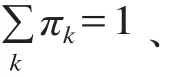
2.1.3 枢纽内部协调能力

枢纽内部协调能力体现在枢纽换乘节点内部交通设计和服务设施通过能力，从枢纽换乘站内部的通畅性、协调性角度评价。

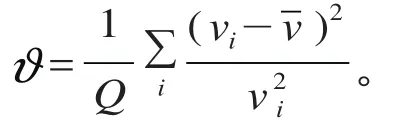
其中，vi为旅客正常行走速度，i 为旅客类型(主要根据旅客年龄划分)；为旅客平均行走速度；Q 为换乘客流量。拥挤分布不均衡度分为时间不均衡度和空间不均衡度。随着列车的到达，站内换乘客流的平均拥挤程度会升高，拥挤时间分布不均衡度和拥挤持续时间将达到较高水平。由于高峰时段旅客集中分布，高速列车进出站口人流分布呈现高密度等级时间分布比例延长的现象。定义拥挤时间不均衡度 Λt、空间不均衡度 Λs和拥挤分布不均衡度 Λ 为

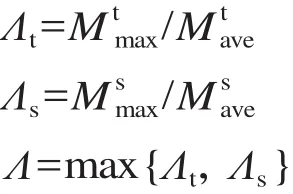
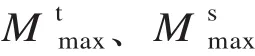
综上所述，定义通畅性指标 μ1为

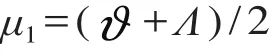
（2）协调性。协调性表现为换乘客流敏感度、设施能力适应度和枢纽组织有序度。

① 换乘客流敏感度 Γ。换乘客流敏感度衡量时效变化趋势对客流规模变化趋势的弹性，客流规模直接影响换乘旅客的走行时间，换乘设施配置属性与客流规模的适应程度反映换乘设施的空间协调水平。定义客流敏感度 Γ 为换乘时间 T 与换乘客流规模 Q 的弹性：Γ = ∂T / ∂Q。

② 设施能力适应度 Θ。换乘客流的到达呈现非连续均衡状态，短时间内可以对换乘设施产生冲击作用。设施能力适应度 Θ 反映客流量大小与设施之间的协调程度，定义为高峰小时客流量 Qg与设施通过能力 C 的比：Θ = Qg/ C。

③ 枢纽组织有序度 Ξ。枢纽组织有序度反映枢纽内部交通组织水平和客流流线之间的协调性。枢纽内分布有进站流、出站流和中转流，不同流线的交织会形成各类大小不同的冲突点。枢纽组织有序度 Ξ 反映枢纽内各种交通流相互干扰的程度，定义为枢纽内不同交通流形成的冲突点 J 与客运专线换乘枢纽面积 S 的比值：Ξ = J / S。

综上所述，定义协调性指标为

根据枢纽内部通畅性和协调性指标，定义枢纽内部协调能力评价指标为

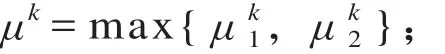
2.2 列车开行特性评价指标

枢纽内不同车站连接的方向不同，当换乘列车开行频率较低，同站换乘等待时间较长时，高出行时间价值的旅客换乘时会选择异站换乘，增加出行的可靠稳定性。换乘旅客出行时，期望选择高频率列车，增加换乘机率。列车开行特性如列车平均运行速度、线路平均运行距离、线路能力均体现在枢纽连通性指标中，在此仅考虑列车衔接率。衔接率η 作为衡量路网列车衔接服务水平的标准之一，反映列车的资源配置能力。衔接率 η 按⑷式计算。

式中：衔接列车数 Nx为在约束时间域内某线路列车能够衔接的列车数；N 为根据某线路列车开行间隔得到的理论开行数。

2.3 旅客出行效用评价指标

枢纽的衔接服务水平是衡量旅客出行效用的重要因素。旅客在选择换乘出行时，会综合考虑个人属性(经济收入、职位、出行目的等)和列车开行技术特性(速度、舒适性、发车时间等)。高出行时间价值的旅客对列车服务等级和频率的要求更高。

2.3.1 换乘次数

枢纽换乘节点衔接线路数越多，旅客越能够以较少的换乘次数到达较多的目的地。在此将同城异站换乘当作一次换乘。枢纽换乘次数可以通过换乘节点的衔接线路数和旅客对异站换乘的接受度来衡量。异站换乘的接受度与乘坐城市交通所需的时间、列车开行频率等有关。换乘次数评价指标定义为

式中：φ 为换算系数。

2.3.2 换乘时间

换乘时间反映旅客对列车衔接服务的接受程度，影响旅客出行效用。换乘时间包括必要的换乘时间与换乘等待时间。必要的换乘时间指到达换乘站的时间(同站换乘)和乘坐城市公共交通的时间(异站换乘)，换乘等待时间指到达换乘站点时间与列车出发时间差。

（1）必要的换乘时间。定义必要的换乘时间 t0= tz+ tg，tz为换乘走行时间，tg为搭乘公共交通所需的时间。tg=0表示同站换乘，tg≠0表示异站换乘。根据 G.Bouladon假设，步行时间 tz与步行距离 Lτ的函数表达式为tz= ε Lτ[5]，ε、τ 为系数。

（2）换乘等待时间。换乘等待时间与列车开行频率和发车间隔有关。对于同站、异站换乘的旅客，换乘等待时间的评价指标不同。

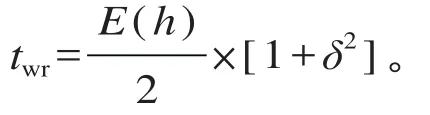
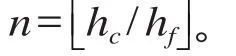
若换乘旅客数超过换乘列车的载客量限制 Cc，部分旅客必须等待下趟列车。需换乘第 k，k∈Z+列车的乘客比例为 Ψk=(pe - kCc)/ pe，pe ≥ kCc。则 t 时刻到达的旅客，其换乘等待时间包括换乘第1列车的等待时间 tw1和换乘第 k 列车的等待时间 tw2，其公式表示如下。

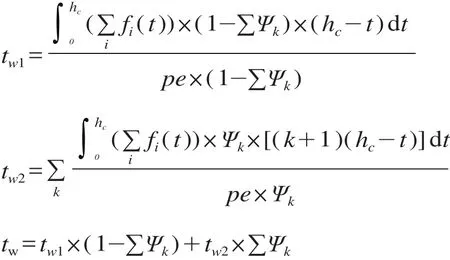
若考虑换乘客流量，设同站、异站换乘客流分别为 QT和 QY，枢纽整体换乘时间为

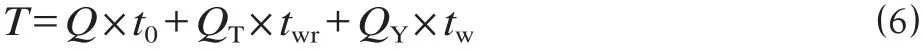
3 枢纽衔接服务水平影响因素相关性分析

3.1 解释结构模型

解释结构模型法(Interpretative Structural Modeling Method，ISM)是现代系统工程中广泛应用的一种分析方法，是结构模型化技术的一种。它主要将复杂的系统分解为若干子系统要素，以定性分析为主，把模糊不清的思想转化为直观的具有良好结构关系的多级递阶结构模型，特别适用于变量众多、关系复杂而结构不清晰的系统分析。具体步骤如下。

（1）设定关键问题。

（2）选择影响关键问题的导致因素。

（3）列举因素之间的相关性。

（4）可达性矩阵。

（5）矩阵分解，建立结构模型。

为此，通过解释结构模型分析枢纽衔接服务影响因素的内部相关性；建立邻接矩阵，识别各要素之间的影响传递关系；对邻接矩阵进行逻辑运算，得到可达性矩阵，形成枢纽衔接服务影响因素的层次递阶结构。

3.2 相关性分析

（1）邻接矩阵。令节点 Vi、Vj(i，j=1，2，…，8)表示各影响因素，两节点之间的相关性用弧(Vi，Vj)表示，两节点之间相连时表示因素 Vi对 Vj有影响，则 aij=(Vi，Vj)=1。设节点 V1、V2、V3、V4、V5、V6和 V7分别表示枢纽路网重要性、枢纽连通性、换乘客流量、换乘时间、换乘次数、枢纽列车衔接率和枢纽内部协调能力；V8为顶层目标，表示枢纽衔接服务水平。上述因素相互影响或间接关联，形成协调性的系统连接图。构建邻接矩阵 A 为

（2）可达性矩阵。可达性矩阵是用矩阵形式反映各顶点之间通过一定路径可以到达的程度。首先将相邻矩阵 A 加上单位矩阵 I，采用布尔代数规则进行乘方运算，A1=(A + I)1，…，An=(A + I)n，直到2个相邻幂次方的矩阵相等为止。若 Am=(A + I)m= Am+1=(A + I)m+1，即为可达性矩阵。经过布尔乘方运算得出

（3）级间分解。对可达性矩阵进行级间分解，得到枢纽衔接服务水平评价系统的多级递阶结构模型。可达集合 R(Vi)，可达矩阵中要素 Vi对应的行中，含有1的矩阵元素所对应的列要素的集合，表示元素 Vi要到达的要素；先行集合 Q(Vi)，可达矩阵中要素 Vi对应的列中，有1的矩阵元素所对应的行要素的集合。交集 R(Vi)∩Q(Vi)，表示可达集合与先行集合的公共元素集合。根据可达矩阵 A3列出可达集合、先行集合与交集表如表1所示。

系统中各要素之间的层级关系，最顶层表示最终目标，往下各层分别为对上一层的解释。层级分解是根据 R(Vi)∩Q(Vi)= R(Vi)条件进行层级抽取。i =8满足条件，表示 V8为系统的最顶层。然后把表中有关8的元素都抽取掉，得到可达矩阵表如表2所示。

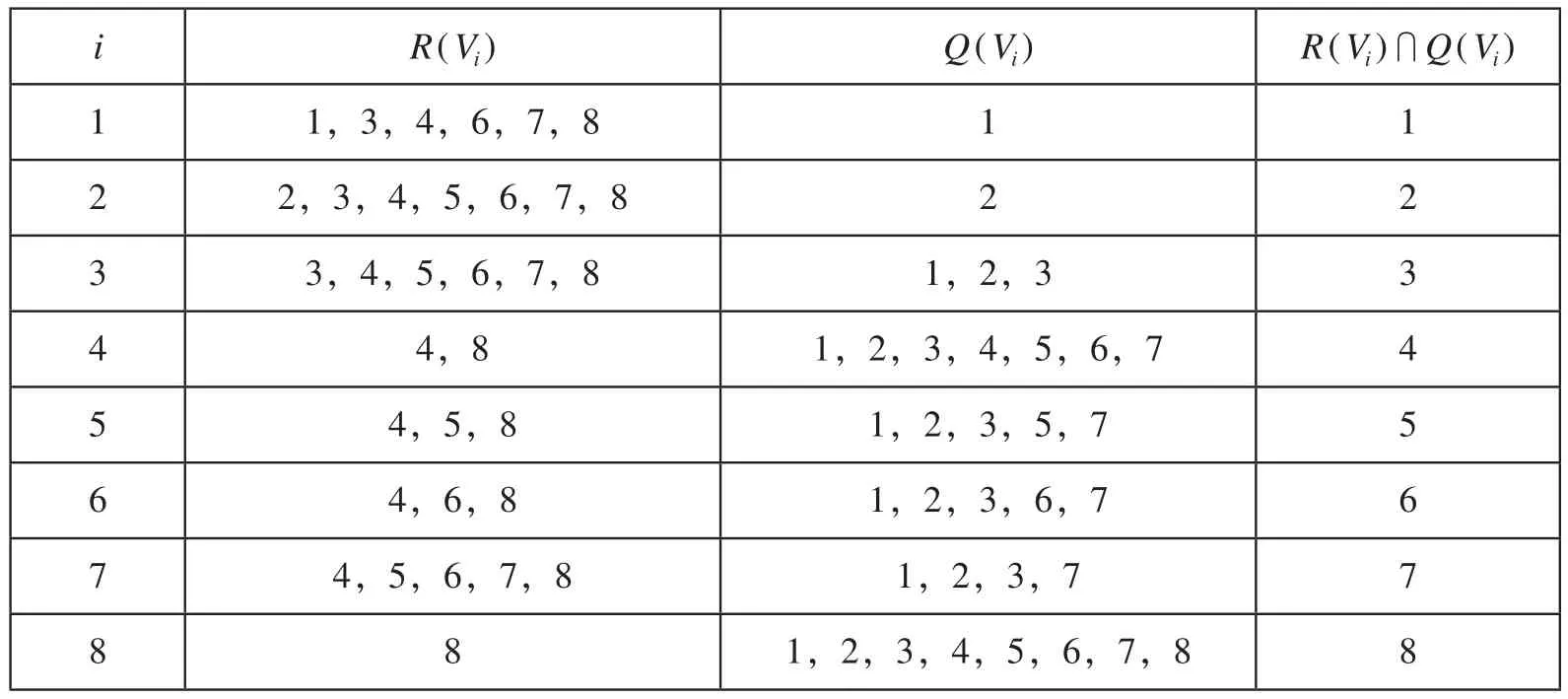
表1 可达矩阵可达集合、先行集合元素表

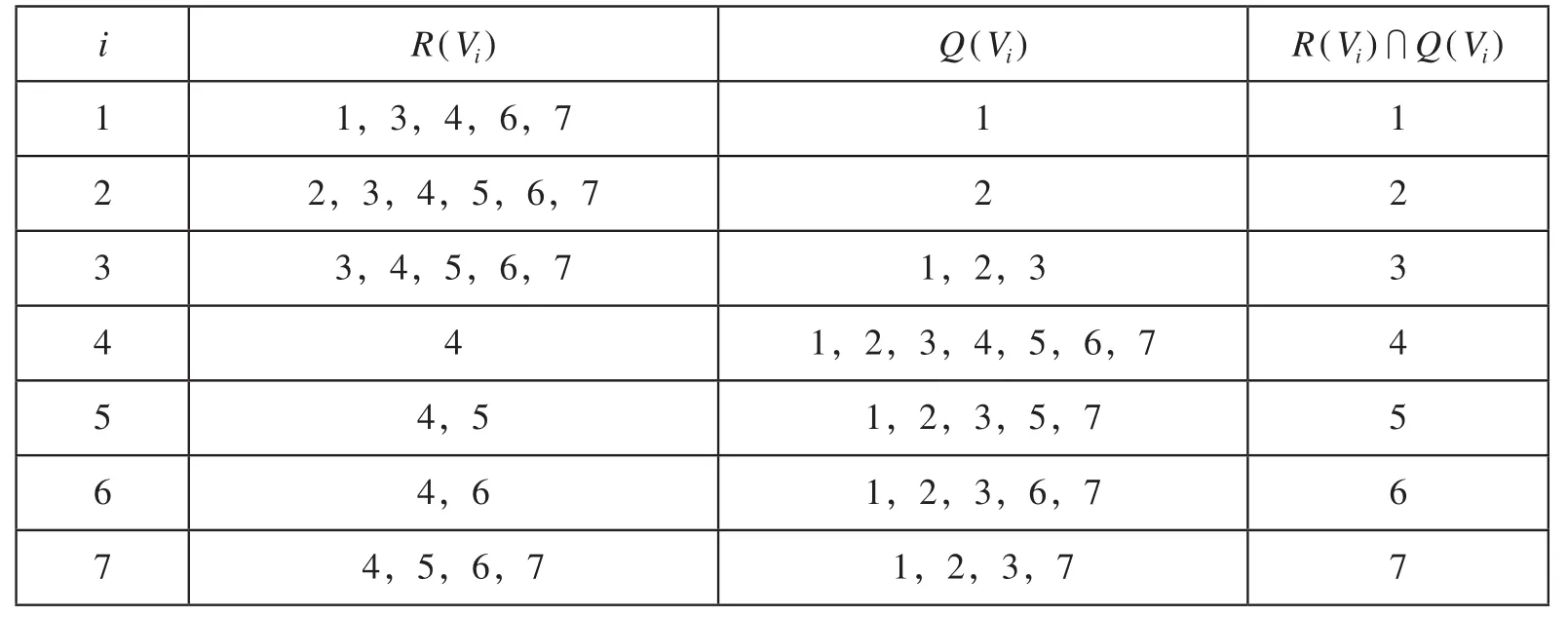
表2 抽取元素8后的可达矩阵表

从表2中可以看出 i =4符合条件，则 V4作为第2层，为 V8的解释。从表中抽取出有关4的元素，依次进行下去，得到枢纽衔接服务水平影响因素之间的层级递阶结构如图2所示。

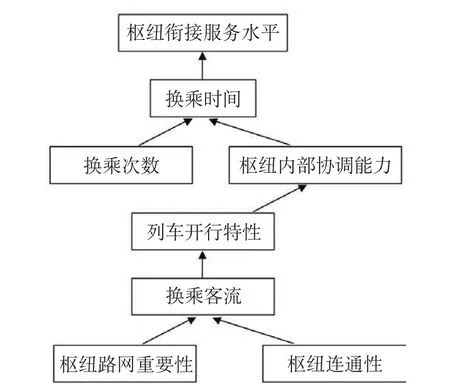
图2 枢纽衔接服务水平影响因素层次递阶结构

由此递阶结构，可以看出衔接服务水平的直接影响因素为换乘时间，换乘时间作为优化换乘服务的重要衡量指标，影响着旅客出行效用。换乘次数决定了总旅行时间，枢纽内部协调能力决定了换乘设施的通过效率；而基本影响因素是枢纽自身条件的枢纽路网重要性和枢纽连通性，枢纽自身属性决定换乘客流量；列车开行方案的编制以“按流开车”为原则，换乘客流量影响列车开行特性；列车开行频率等决定枢纽协调性，以满足服务能力与客流量的匹配。

4 结束语

在建立衔接服务水平影响因素评价指标的基础上采用解释结构模型对影响因素进行层次分析，明确了各因素之间的相互关系。该评价体系有利于进一步分析各因素的影响权重，从而确定衔接服务水平的关键因素；通过判断枢纽衔接服务水平与客流需求的适应性、旅客换乘高效性，为制订列车衔接方案提供基础依据。为此，需要进一步根据影响因素的协调权重，优化最关键因素，使整个路网的衔接能力最优。同时，需要通过实际数据，具体分析路网中各枢纽衔接服务水平，提出改善措施。

：

[1]Spring C. Hsu. Determinants of Passenger Transfer Waiting Time at Multimodal Connecting Stations[J]. Transportation Research Part E，2010(45)：404-413.

[2]P. Vansteenwegen，D. Van Oudheusden. Decreasing the Passenger Waiting Time for An Intercity Rail Network[J].Transportation Research Part B，2007(41)：478-492.

[3]张 铭，徐瑞华. 轨道交通网络列车衔接组织的递阶协调优化[J]. 系统工程，2007，25(9)：33-37.

[4]Sabyasachee Mishra，Timothy F. Welch. Performance Indicators for Public Transit Connectivity in Multi-modal Transportation Networks[J]. Transportation Research Part A，2012(46)：1066-1085.

[5]郭 瑾. 高速铁路综合枢纽换乘条件评价及应用研究[D].北京：北京交通大学，2011.

[6]韩宝明，李得伟，张 琦，等. 铁路客运专线换乘枢纽交通设计理论与方法[M]. 北京：北京交通大学出版社，2010.