大型液压离心振动台的耦合特性分析

罗中宝，杨志东，丛大成，张 兵

(哈尔滨工业大学 机电工程学院，哈尔滨 150001)

为了研究地震环境下的土动力学特性、地基液化、边坡稳定性、泥土-地基-结构间的耦合关系，发达国家相继建成了一系列大型离心振动台，这些离心振动设备在其本国土工领域发挥着举足轻重的作用[1]。鉴于中国严峻的地震形势和土工领域研究的迫切需求，中国地震局工程力学研究所联合哈尔滨工业大学，正在研制国内第一大、世界第二大单轴离心振动台[2]。

土工岩土材料，其动态特性都具有很强的非线性，这些特性与岩土应力、岩土应力历史密切相关。离心机可以提供一个离心加速度场来补偿物理原型的自重应力。通过对岩土自重应力的补偿，可利用小比尺物理模型来精确模拟实际工程原型在地震激励下的响应。与此同时，离心振动试验也提供了解释岩土变形、结构失效等问题的试验数据，这些数据可以为岩土动力学模型的推导及修正提供依据。因此，离心振动台被认为是当今世界土工抗震领域最先进、最有效的试验设备之一。

世界上已建成的土工离心振动台约有25台，国外最具代表性的研究机构包括美国加州大学戴维斯分校、美国科罗拉多大学和美国伦斯勒工学院；国内最具代表性的研究机构包括南京水利科学研究院、清华大学和香港科技大学[3]。相比而言，国内振动台在振动负载、振动加速度、振动频宽等方面，与国外先进水平有较大差距。而国外的振动台研制时间较早，现阶段的工作重心已从振动台的研制转移到土工离心实验上来，所以国内外关于大型离心振动台研制的可用资料相对较少。总的来说，离心振动台相比普通振动台而言，受以下两方面因素的影响：① 受离心机装机容量的限制，振动台基础的质量和刚度有限；② 受离心振动复合环境的影响，振动台中液压元件的动态特性发生改变。鉴于上述影响因素，在离心振动台的研制过程中需着重解决以下三方面问题：① 轻柔基础、液压执行机构、岩土模型的耦合特性分析；② 离心振动复合环境对液压元件的影响，特别是对三级电液伺服阀动态特性的影响；③ 离心振动台控制策略的研究。针对以上三方面问题，国内外学者已进行一些研究。

目前，三级伺服阀在离心力振动复合环境下的特性分析研究，几乎处于空白。但前人关于两级伺服阀在离心力环境下的特性分析经验值得借鉴。贺云波根据伯努利方程和流体冲量定理，分析了两级电液伺服阀在离心工作环境下的输入电流与阀芯位移间的关系。文中指出当伺服阀顺臂安装时，离心加速度与伺服阀的零偏电流近似成正比[4]。董云雷也对该问题也进行了深入研究，并分析了离心力场下的油液传输特性，提出了离心液压的概念[5]。

由于离心振动实验的持续时间非常短，一般采用三状态控制的伺服控制策略来提高位置闭环系统的频宽，采用离线迭代的振动控制方法来校正振动台的驱动信号。Ketcham等[6]提出了这种对驱动信号的校正算法，用以提高离心振动滑台对高频加速度信号的复现能力。Mason等[7]阐述了UCD-CGM实验中心最近一系列土工离心实验中所使用参考信号的选择方法及对应的过滤过程。Mason也采用离线迭代频响函数的方法来校正驱动信号，实验表明该方法可使振动台输出信号与参考信号近似达到一致。

相比问题②、③而言，轻柔基础、执行机构、岩土模型的耦合特性是研究②、③问题的基础，是现阶段离心振动台研究最需解决的问题。Fiegel等[8-9]定性评价了小比尺模型、模型箱和振动台之间的耦合关系。Ketcham[10]在研制科罗拉多的离心振动滑台时，也发现了在滑台运动时，吊篮响应具有低、高频共振的特点。此后，Ilankatharan[11]定量分析了离心振动台中液压执行机构、岩土模型和轻柔基础间的动态耦合，并采用Opensees工具对该耦合关系进行仿真。但是，前人研究都没能准确建立起轻柔基础、执行机构、岩土模型的耦合数学模型。本文将集中解决该问题，详细推导并分析轻柔地基、执行机构、岩土模型的耦合关系。

1 离心振动系统简介

图1是香港科技大学离心振动系统(HKUST)的结构示意图。如图所示，离心振动系统大致可分为以下6部分：① 吊篮及振动台系统；② 转臂；③ 平衡配重；④ 驱动电机；⑤ 变速箱；⑥ 离心机主轴。驱动电机带动离心机主轴旋转，主轴的旋转速度受变速箱调控；离心机主轴经转臂支撑带动转臂旋转，使振动台上的岩土模型处于离心力场中，达到补偿物理原型自重应力的目的。振动台系统随吊篮一起做离心运动，可以不停机地连续触发多次地震波。

如图2所示，图中为哈工大与中国地震局工程力学研究所联合研制的单轴离心振动台，其离心机的装机容量为300 gt，最大离心加速度为100 g，最大振动负载1 500 kg，最大振幅12 mm，最大水平加速度为30 g，最大振动频率为350 Hz。该离心振动台包括以下6部分：① 吊篮；② 伺服阀及液压缸；③ 上平台；④ 剪切轴承；⑤ 支撑板；⑥ 蓄能器。各部分的详细情况如下。

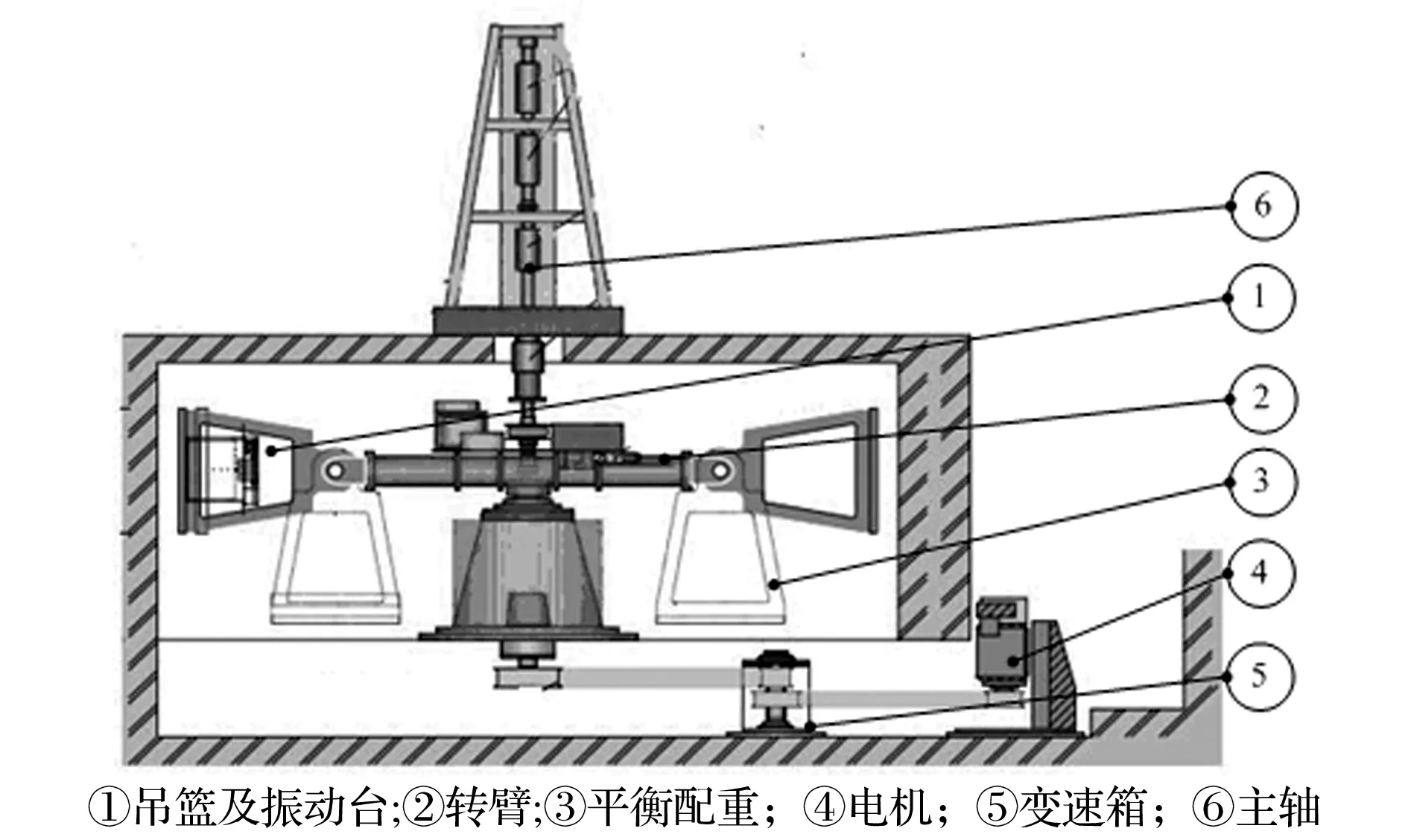
图1 离心振动系统示意图

图2 哈工大、中国地震工程力学研究所联合研制的离心振动台

① 吊篮：吊篮的材质为Q345，包括2个吊耳和1个底座；吊篮通过2个吊耳与离心机臂相连，底座的内部做成栅格状，以减少底座重量。

② 支撑板：支撑板固定在吊篮上，用以安装蓄能器、液压缸、伺服阀和剪切轴承；在支撑板内部钻有油孔，用以整个液压系统的供油和回油。

③ 蓄能器：离心振动台配备了4台蓄能器，作为短时间激振的油源使用；这种供油方式相比通过地面油源供油而言，减少了离心力对液压系统的影响。

④ 剪切轴承：支撑板与上平台间安装了28个橡胶剪切轴承，用来支撑上平台、岩土模型的离心负载。

⑤ 液压缸与伺服阀：离心振动台所采用的伺服阀是哈尔滨工业大学自行研制的大型三级伺服阀，液压缸采用两条非对称液压缸做一条对称液压缸使用，原理图如图3所示。另外，液压缸与上平台之间添加凹形运动块，允许上平台绕几何中心做小幅转动。

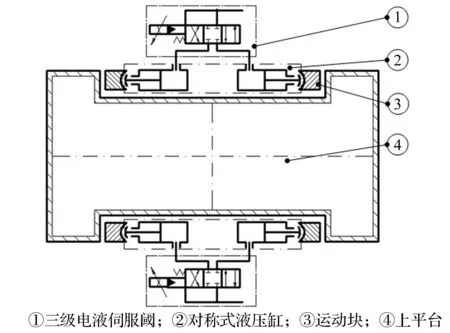
图3 离心振动台中使用的液压缸和伺服阀

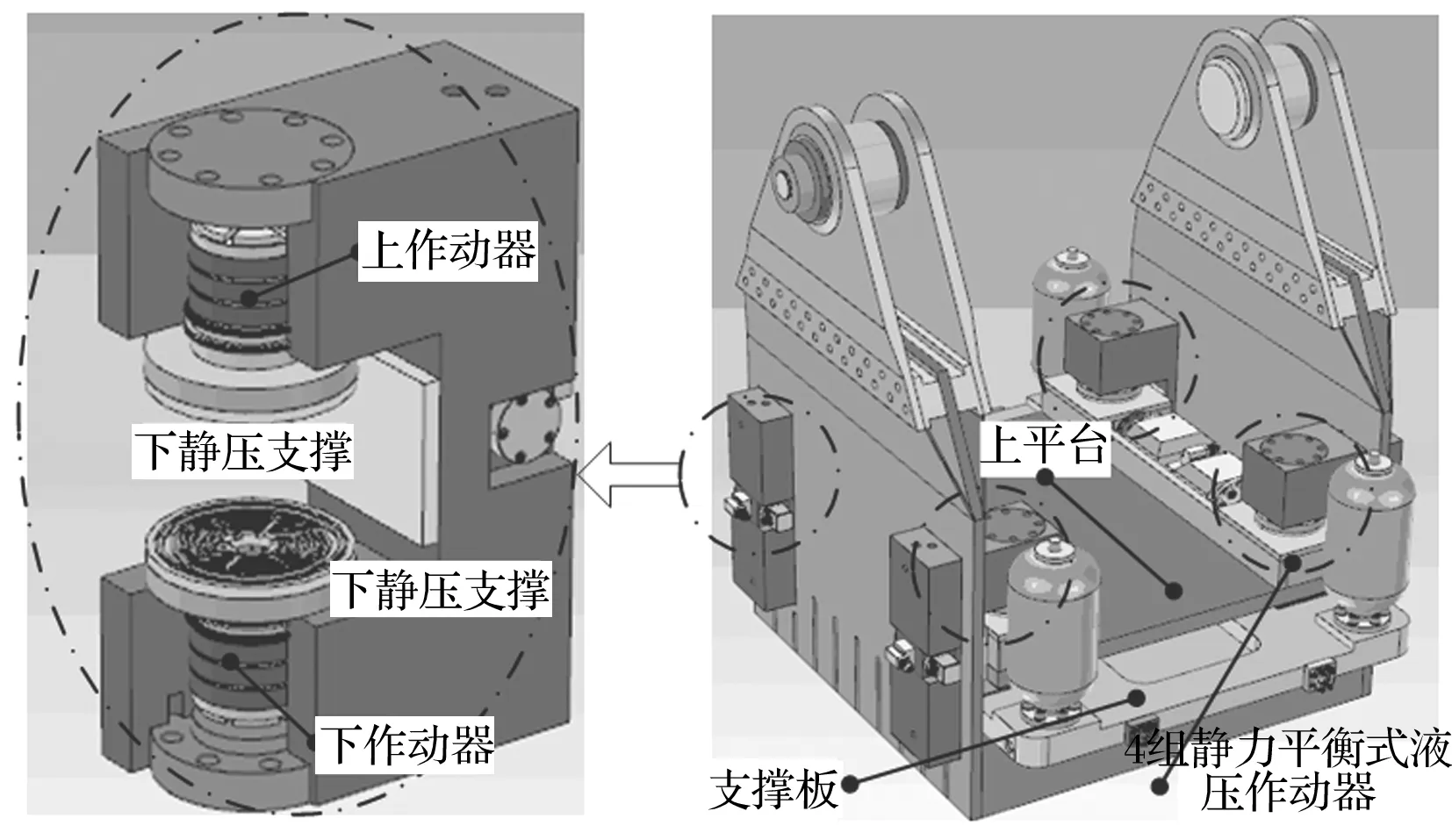
图4 离心振动台中使用的静力平衡式液压作动器

除此之外，由于剪切轴承在大位移运动时的水平向弹性力非常大，严重影响了离心振动台波形复现的精度。哈尔滨工业大学正在研制静力平衡式液压作动器来代替橡胶剪切轴承，其三维实体模型如图4所示。文中的静力平衡式液压作动器由一组不完全平衡型静压支撑和一组液压作动器构成。通过控制作动器的出力差，达到抵消离心力的目的。由于不完全平衡型静压支撑的摩擦系数仅为0.002 5～0.003，因此该支撑方式还可大大减小上平台运动过程中的摩擦力。对于一个静压支撑而言，上平台与静压支撑紧密配合，作动器出力的90%由支撑中的高压油膜支撑，10%由支撑的密封圈承受。总的来说，通过在离心振动台中引入静力平衡式液压作动器可抵消离心力，并减小水平激振过程中的摩擦力。此外，该支撑方式也可以作为垂向激振使用，为单轴离心振动台向水平、垂直双向离心振动台的改造提供条件。

2 轻柔基础动态特性的等效

为了理论推导的方便，将轻柔基础简化为连续质量弹簧；由于离心振动台中包含两套执行机构，每套执行机构所对应轻柔基础的质量为整个吊篮质量的一半，上平台质量也为振动台台面质量的一半。如图5所示，液压缸缸筒固定在轻柔基础上，缸筒随轻柔基础的变形而产生位移。连续质量弹簧在液压缸反力(F1,F2)的作用下，会产生与上平台振动方向相反的加速度，并发生一定量的弹性变形。为了便于系统传递函数的推导，希望将轻柔基础的动态特性等效成图5中所示的一维质量-弹簧-阻尼系统。在等效过程中需遵循以下三点原则：① 等效质量-弹簧-阻尼系统的固有频率与连续质量弹簧的一阶固有频率保持一致；② 等效质量-弹簧-阻尼系统中轻柔基础的加速度方向与上平台的振动方向相反，加速度大小与基础质量成反比；③ 激振频率保持一致，对于图2中的离心振动台而言，动态激振力主要为剪切轴承变形引起的弹性力。在下面的内容中，将详细叙述该等效模型的推导过程。

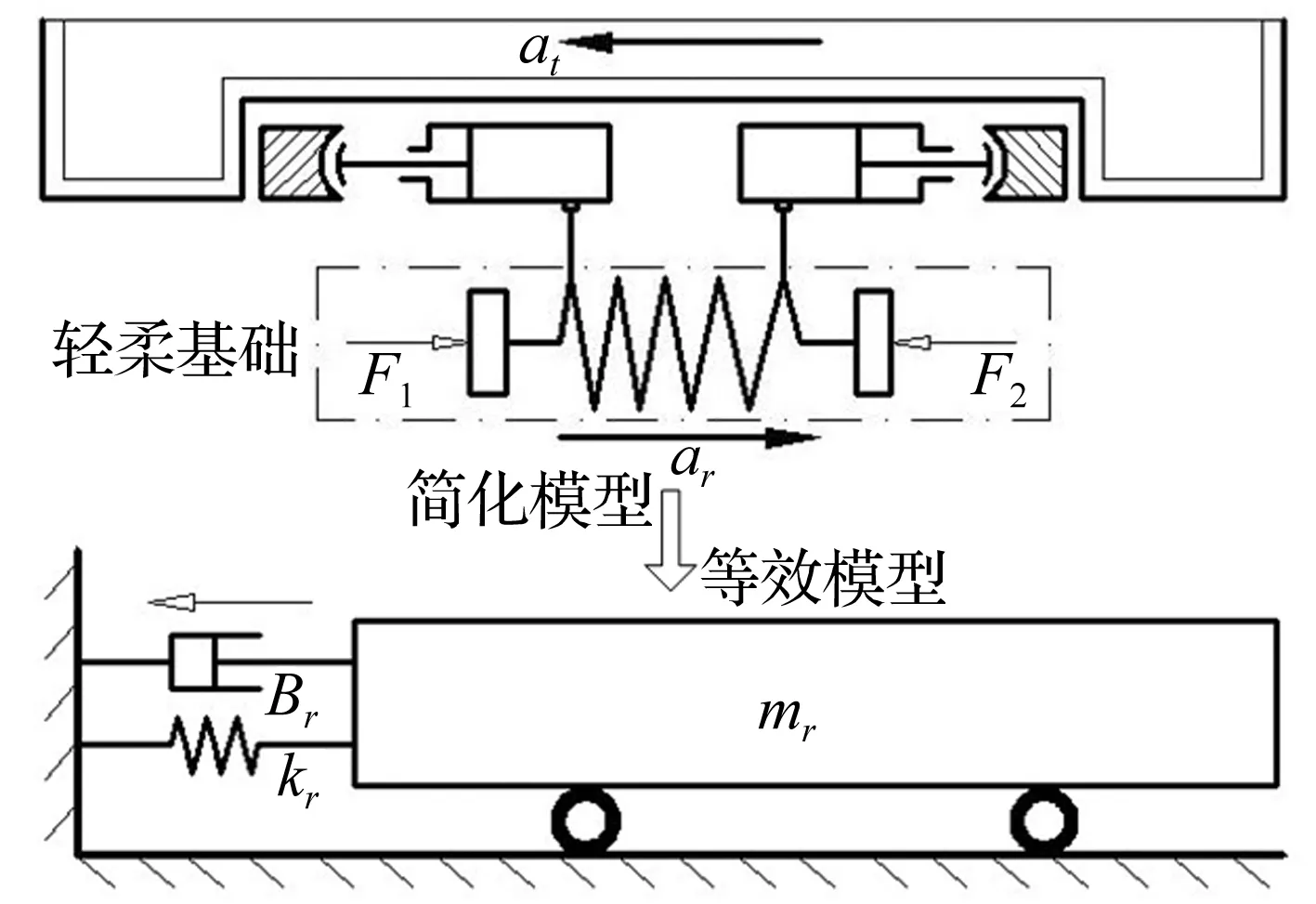
图5 轻柔基础与液压执行机构的耦合关系

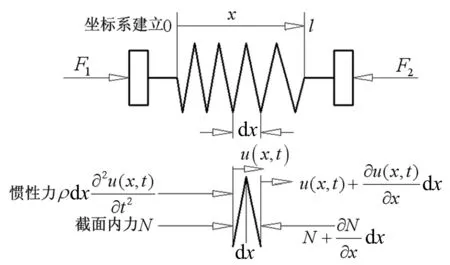
图6 连续质量弹簧的受力分析

仅考虑连续质量弹簧在水平方向上的变形，建立如图6所示的坐标系。任取一小微元作为研究对象，根据达朗贝尔原理可得(令F1>F2)：

(1)

式中，ρ表示连续质量弹簧的线密度；u(x,t)表示位置x处质点的运动；N表示弹簧截面处的内力。

化简上式可得：

(2)

其中，截面内力N可根据胡克定律进行计算：

(3)

式中，k表示连续质量弹簧的整体刚度；l表示弹簧的长度。

因此，将式(3)代入式(2)，可得连续质量弹簧的运动控制方程：

(4)

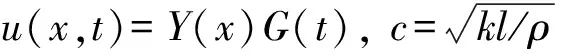
(5)

令等式两边都等于-(ω/c)2，可得：

(6)

上述常微分方程的通解可以表示为：

G=Csinωt+Dcosωt

A,B,C,D由边界条件和初始条件所确定。文中的连续质量弹簧，满足以下三个边界条件。

(1) 左端点的力边界条件

(2) 右端点的力边界条件

(Csinωt+Dcosωt)

又因为F1+F2=PsAp，其中Ps表示油源压力，Ap表示活塞的有效作用面积。因此可得：

然后上式两端分别对时间求导数：

(7)

(3) 中间点的力边界条件

同样，等式两边同时对时间求倒数，可得：

(8)

联立式(7)、式(8)便可求得系统的固有频率。观察式(7)、式(8)，在B=0的情况下，系统的固有频率可表示为：

i=0,1,2,…

(9)

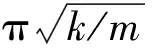
如前所述，系统的激振力主要是剪切轴承变形引起的弹性力。由于离心振动台中安装了28个剪切轴承，振动时每个剪切轴承的变形量也不同，因此很难准确估算系统各个激振力的大小，但各激振力的频率是可近似估算的。众所周知，弹性力与上平台、轻柔基础间的相对位移成正比，液压缸出力却与上平台的绝对加速度成正比。据此，剪切轴承变形引起的弹性力的频率与液压缸出力的频率近似相同。因此，在等效模型中使用液压缸出力作为激振力，来模拟轻柔基础在外载荷激励下的响应。表面上看来，如此等效激振力并不是非常精确，但从本质上来说这种等效方式却准确模拟了轻柔基础共振时的极限情况。当液压缸出力的频率与轻柔基础任一固有频率重合时，在弹性力的作用下，轻柔基础发生共振，轻柔基础上任一点的位移都近似无穷大，此时激振力的大小并不重要，激振力的频率起主导作用。因此，相比准确等效激振力的大小而言，准确模拟激振力的频率显得更为重要。

3 耦合传递函数的推导

(1) 滑阀的流量方程

假设：滑阀为理想零开口四通滑阀，四个节流窗口是匹配、对称的；节流窗口处的流动是紊流，流体压缩性在阀内予以忽略；油源压力恒定不变，回油压力近似为0。此时，滑阀的流量方程可表示为式(10)：

qL=kqxv-kcpL

(10)

式中，qL表示滑阀的负载流量；kq表示滑阀的流量增益；xv滑阀的阀芯位移；kc滑阀的流量-压力系数；pL负载压降。

(2) 流量连续性方程

假设：液压缸每个工作腔内各处压力相同，油液温度和体积弹性模量认为是常数；液压缸的内、外泄漏为层流流动。此时，流量连续性方程表示为式(11)：

(11)

式中，Ap表示液压缸活塞的有效作用面积；xt表示上平台的绝对位移；xr表示轻柔基础的绝对位移；ctp表示总泄漏系数；Vt表示总压缩体积；βe表示油液的体积弹性模量。

(3) 力平衡方程

假设：忽略模型箱的动态特性，忽略岩土模型与模型箱间的摩擦力；上平台与剪切轴承之间的摩擦力也忽略不计。 此时，分别以轻柔基础、上平台和岩土模型的整体、上平台为研究对象，根据牛顿第二定律，建立式(12～14)的力平衡方程。

脉岩多呈北西向及北东向产出，主要类型有细粒花岗岩脉、花岗斑岩脉、闪长玢岩脉、安山玢岩脉、英安玢岩脉等。

首先，以轻柔基础为研究对象，进行受力分析，可得式(12)：

(12)

式中，mr表示轻柔基础的质量(包括缸筒质量)；xr表示轻柔基础的位移；Br表示等效模型的阻尼；kr表示等效模型的刚度。

然后，以上平台和岩土模型的整体为研究对象，进行受力分析，可得式(13)：

(13)

式中，mt表示上平台的质量；ms表示岩土模型的质量；xs表示岩土模型在上平台上的相对位移。

最后，单独以上平台为研究对象，进行受力分析可得，可得式(14)：

(14)

式中，Bs表示岩土模型的阻尼；ks表示岩土模型的刚度。

(4) 几何补充方程

实际系统中，位移传感器的两端分别固定在缸筒和上平台上，其测量的是轻柔基础与上平台之间的相对位移，因此位移传感器的输出位移y满足式(15)中的几何关系：

y=xt+xr

(15)

将式(10)～式(15)进行拉普拉斯变换，利用其变换结果便可得到考虑轻柔基础、液压执行机构、岩土模型耦合特性的系统传递函数，其方框图如图8所示。为了便于公式的推导，定义如下变量：

总的流量-压力系数：kce=kc+ctp；

经详细推导，位移传感器输出y与阀芯位移xv间的传递函数，最终可表示为如式(16)所示：

(16)

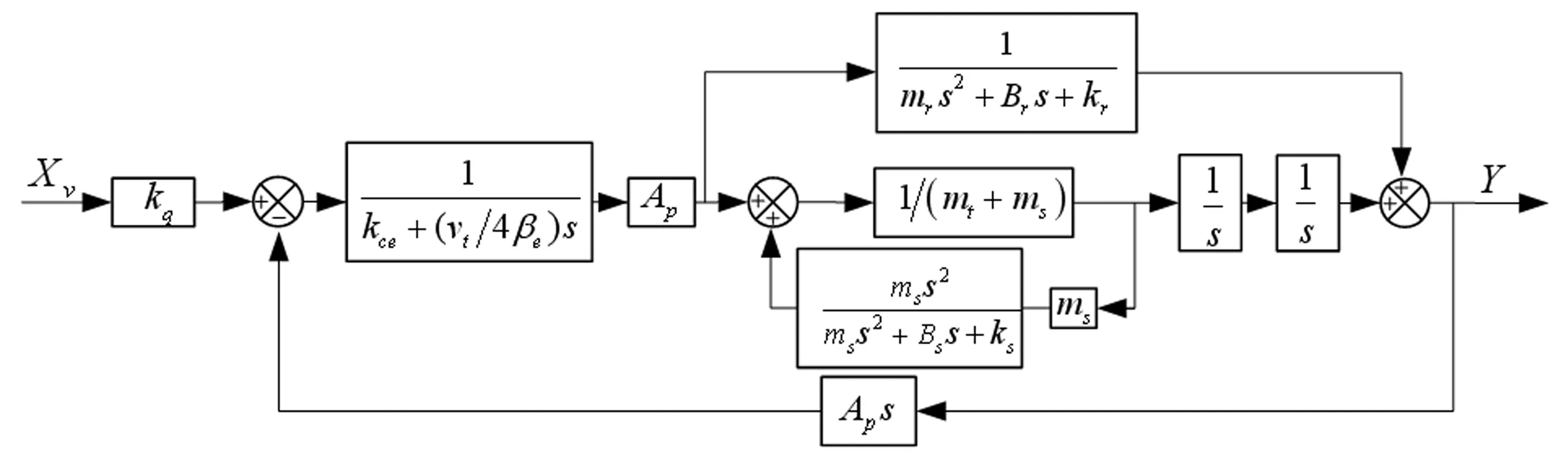
图8 耦合系统的传递函数

式中ωrts、ξrts、ωrts′、ξrts′由方程组式(17)确定。根据式(16)和式(17)，当满足mr远大于(mt+ms)、kr→∞的边界条件时，W(s)=W′(s)，系统的传递函数可简化为仅有惯性负载时理想对称阀控制对称缸的传函形式。

(17)

4 耦合传递函数的仿真分析

根据文中第二部分轻柔基础动态特性的等效方法，求取了等效一维质量-弹簧-阻尼系统的固有频率、阻尼比。再结合实际离心振动台中液压执行机构的实际参数，对系统的耦合特性进行仿真，仿真参数如表1所示，所有仿真参数已经过一定圆整。

在不考虑伺服阀动态特性的情况下，伺服阀输入电压与阀芯位移xv成正比，位移传感器输出y与伺服阀输入电压之间的传递函数如图9所示。如图9，系统的幅频、相频特性都具有明显的波峰波谷。如曲线1所示，在低频段(10～100 Hz)，耦合系统的幅频特性近似按照-20 dB/dec下降，与理想积分环节类似。原因如下：如式(16)所示，耦合系统包括7个极点、4个零点。低频段的两对零、极点，距离非常接近，具体来说，极点-17.7±296i与零点-13.6±304i距离很近；极点-9.64±622i与零点-9.63±623i几乎可以完全抵消。因此，在低频段，耦合系统特性与理想积分环节类似；另外，在高频段(100～1 000 Hz)，耦合系统的谐振频率为363 Hz，远大于不考虑耦合特性的液压固有频率(187 Hz)。另外，比较曲线1和曲线2可得：当岩土模型的固有频率发生改变时，曲线2在(45～100 Hz)范围内，幅频特性变化剧烈，不能近似等效为积分环节。这也从侧面说明岩土模型动态特性对耦合系统特性有较大影响。在实际的地基液化实验中，岩土模型的刚度(或固有频率)在实验过程中逐渐降低，耦合系统的动态特性也随之发生改变。

表1 耦合系统的仿真参数

在不考虑伺服阀动态特性的情况下，上平台绝对位移xt与阀输入电压间的传递函数如图10所示。相比于不考虑耦合关系时液压执行机构的传递函数，考虑耦合关系的传递函数的幅频、相频特性具有明显的波峰波谷。如图10所示，幅频特性在50 Hz和100 Hz处，幅度突然增大，这说明传递函数分子包含两个固有频率分别为50 Hz和100 Hz的二阶微分环节，相比图9中曲线1的传递函数而言，上平台绝对位移xt与阀输入电压间的传递函数中又引入了一组不可对消的零极点。

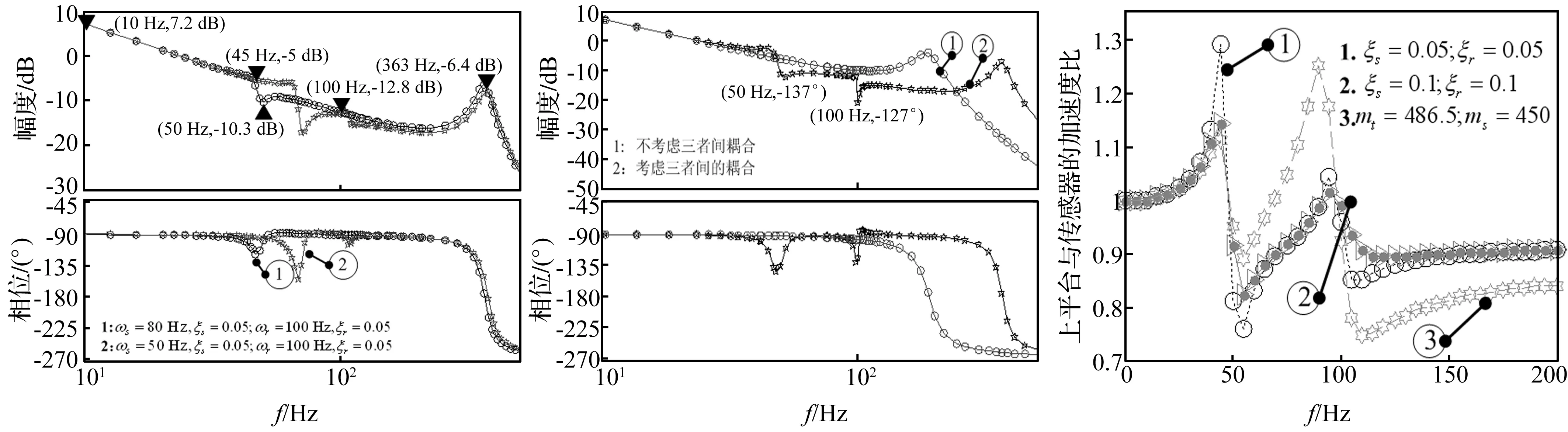
图9 耦合系统的传递函数

离心振动台是通过位移传感器进行位置闭环，而实际控制量是上平台的绝对加速度，因此需要研究上平台绝对加速度与位移传感器二阶微分之间的关系。为叙述的方便，将位移传感器输出的二阶微分定义为传感器的加速度。如图11所示，上平台、传感器的加速度比与频率密切相关，上平台加速度at(s)与传感器加速度a(s)间的传递函数可表示为式(18)所示：

(18)

由传递函数可得，在ωs、ωr频率附近，二者加速度比达到极小值，此结论在图11中也得到了验证。文中从能量角度来解释该现象：从能量的角度来讲，在岩土模型和轻柔基础的固有频率附近，岩土模型和轻柔基础发生共振，其运动占据了系统的大部分能量，此时上平台的所占能量相对较少，因此此时加速度比到达极小值。同理，在耦合固有频率ωrts、ωrts′处，二者加速度比达到最大值，此时上平台达到共振，其运动占据了系统大部分能量。与此同时，从图11中还可以看出：岩土模型、轻柔基础的阻尼比对二者加速度比的影响较大，阻尼比越小二者加速度比变化越激烈；另外，在150 Hz以上的高频段，二者加速度比趋于恒定值。当mt=286.5 kg、ms=650 kg时，二者加速度比值为0.918；当mt=486.5 kg、ms=450 kg时，二者加速度比值为0.868。该结论可以通过式(18)来进行验证，当ω→∞时，二者之间的比值与上平台的质量成反比，上平台的质量越大，二者加速度比值越小。为了在上平台上精确复现加速度信号，应该尽量减小上平台的质量，使上平台加速度与传感器加速度更加接近。此时，通过传感器的位置闭环，便可以使上平台的加速度满足要求。

5 离心振动台伺服控制策略的研究

如图12所示，离心振动台的伺服控制策略主要包括以下四部分：① 自由度分解与自由度合成；② 前置滤波器；③ 三状态反馈；④ 顺馈控制器。下面将对上述四部分的作用及设计原则作简要说明，详细信息见文献[12]。

(1) 自由度分解、合成矩阵。自由度分解矩阵是将自由度位置偏差信号转换为两个单系统的偏差信号，驱动相应的激振器运动。自由度合成矩阵是将两个单系统的反馈信号(位置、速度和加速度信号)转化为自由度反馈信号。对于图2中的离心振动台而言，包括以下两个自由度：① 沿水平方向上的平动；② 沿上平台中心的转动。在振动台工作时，仅希望振动台沿水平方向平动，不允许平台绕中心转动，绕中心转动自由度的参考信号始终为0。离心振动台的自由度分解Hf、合成矩阵Hh可表示式(19)所示。

(19)

(2) 前置滤波器。前置滤波器分为两部分：① 利用高通滤波器对低频加速度信号进行滤波；② 利用积分环节将加速度信号转换为位置信号。本文前置滤波器的转折频率设定为10 Hz，其传递函数如下式所示：

(20)

式中ar、xr分别表示振动台的加速度、位置参考，ω0=62.8 rad/s、ξ0=0.5。

(3) 三状态反馈。三状态反馈控制器引入加速度反馈来提高系统的阻尼比，通过对阻尼比的补偿，可以进一步提高系统增益，从而达到提高系统频宽的目的。引入速度反馈也可以提高系统频宽，但速度反馈会降低系统的阻尼比。文中离心振动台的三状态反馈参数如下：加速度反馈系数ka=0.002 7，速度反馈系数kv=0.05，位移反馈增益kv=0.666 7，闭环前置增益ku=7.6。加入三状态反馈前后，传感器加速度与参考加速度间的传递函数如图13所示。加入三状态反馈以后，系统液压固有频率处的阻尼比显著增大，谐振峰幅值显著减少。另外，系统的频宽也从45 Hz左右提升至液压固有频率附近(190 Hz)。

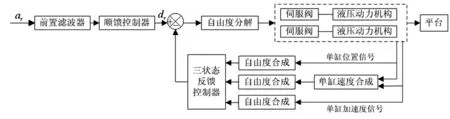
图12 伺服控制策略的原理简图

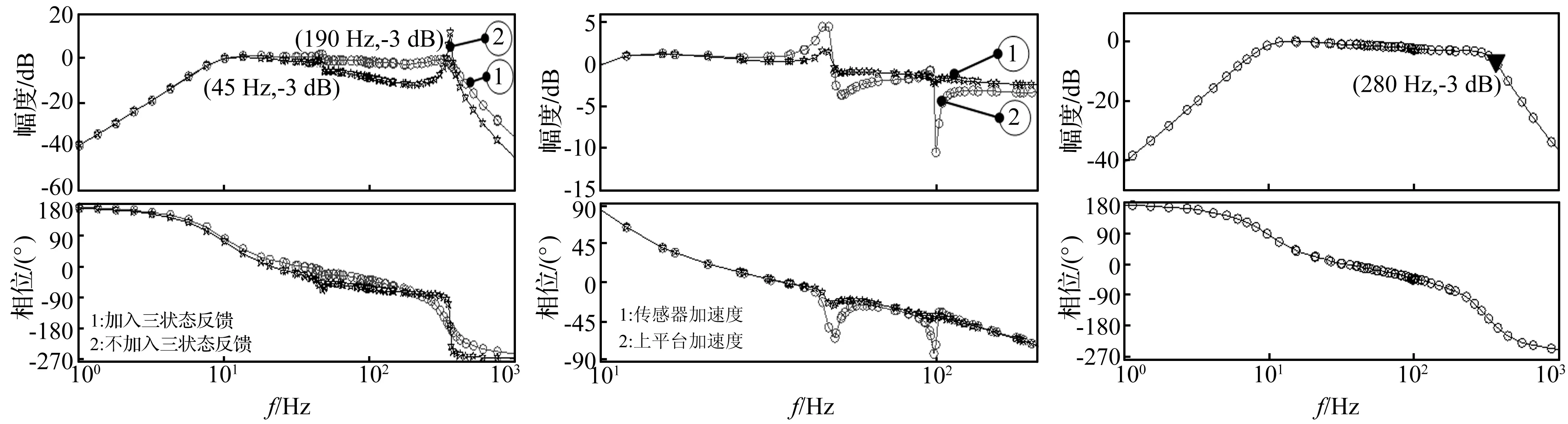
图13 三状态反馈对系统性能的影响

(4) 顺馈控制器。顺馈控制器的目的是对消闭环系统的主导极点，达到提高系统频宽的目的。在离心振动台中，控制目标是上平台的加速度，而不是位移传感器的加速度，上平台、传感器加速度在10～200 Hz范围内的对比图如图14所示。从图14中可以看出，由于零极点没有完全对消，严重影响了系统的频宽。通过辨识系统闭环传递函数，设计顺馈控制器来对消频宽范围内的零极点，顺馈控制器GFF如式(21)所示。

(21)

经过前馈控制器对消零极点后，上平台加速度与参考加速度间的传递函数如图15所示。如图15所示，系统的频宽提高到10～280 Hz。

6 结 论

文中研究了离心振动台中轻柔基础、液压执行机构、岩土模型的耦合关系，完成了以下三方面的工作：① 将轻柔基础简化为连续质量弹簧，推导了轻柔基础固有频率的估计方法，并给出了轻柔基础动态响应的等效方法；② 推导轻柔基础、液压执行机构、岩土模型的耦合数学模型，给出了位移传感器输出与伺服阀阀芯位移间的传递函数；③ 研究了离心振动台的伺服控制策略，通过前置滤波器、三状态反馈、顺馈控制器的设计，可使离心振动台复现频宽范围内的高频加速度参考信号。

虽然文中已经得到一些有用的结论，但是离心振动台中还存在诸多亟待解决的问题：

(1) 离心振动复合环境对液压元件的影响。本文在研究轻柔基础、液压动力机构、岩土模型的耦合关系时，没有考虑离心振动复合环境对液压元件的影响。由于振动台振动方向与离心力方向垂直，因此离心力在液压缸上产生附加负载较小，应主要考虑离心力对三级电液伺服阀的影响。文中将电液伺服阀简化为一个比例环节，与实际情况不符。因此，下阶段应重点研究在离心振动复合环境下三级电液伺服阀垂臂安装时的动态特性。

(2) 轻柔基础固有频率的估计。文中为了理论推导的方便，将轻柔基础等效为连续质量弹簧。但实际轻柔基础为减少质量，做成了栅格状，很难通过理论推导得到轻柔基础的固有频率。从文中的推导也可以看出，轻柔基础的动态对系统性能有较大影响。因此，希望在后续研究中，能够引入实验模态分析的方法来辨识轻柔基础的固有频率。

(3) 顺馈控制器的设计。文中顺馈控制器的设计依赖于对系统闭环传递函数零极点的准确辨识。在实际情况中，离心振动台系统由于岩土模型的变形、蓄能器压力降低等原因，本身就是一个非线性时变系统，因此很难完全通过顺馈控制抵消掉频宽内的零极点。在实际的研制过程中，还需引入鲁棒控制策略来保证在一定系统参数变化范围内，系统能够稳定并达到一定性能。

[1]张建民, 于玉贞, 濮家骝, 等. 电液伺服控制离心机振动台系统研制[J]. 岩土工程学报, 2004, 26(6): 843-845.

ZHANG Jian-min, YU Yu-zhen, PU Jia-liu, et al. Development of a shaking table in electro-hydraulic servo-control centrifuge[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845.

[2]王永志. 振动离心机系统工作原理与初步设计[D]. 哈尔滨: 中国地震局工程力学研究所, 2010.

[3]Wilson D W, Boulanger R W, Feng X, et al. The NEES geotechnical centrifuge at UC DAVIS[C]// 13th World Conference on Earthquake Engineering. Vancouver:Prentice-Hall, 2004.

[4]He Y B, Chua P S K, Lim G H. Performance analysis of a two-stage electrohydraulic servovalve in centrifugal force field[J]. Journal of Fluids Engineering, 2003, 125(1): 166-170.

[5]董龙雷. 离心力-振动复合力学环境的模拟与控制[D]. 西安: 西安交通大学, 2004.

[6]Ketcham, Ko H Y, Sture S. Performance of an earthquake motion simulator for a small geotechnical centrifuge[C]// Centrifuge 91. Rotterdam:Balkema, 1991.

[7]Mason H B, Kutter B L, Bray J D, et al. Earthquake motion selection and calibration for use in geotechnical centrifuge[C]// ICPMG 2010. Rotterdam:Balkema, 2010.

[8]Fiegel G L, Idriss I M, et al. Effect of model containers on dynamic soil response[C]// Centrifuge 94. Rotterdam:Balkema, 1994.

[9]Narayanan. Modeling the seismic response of stratified soil (Graduate Dissertation)[D]. Davis: UC Davis, 1999.

[10]Ketcham. Development of an earthquake motion simulator for centrifuge testing and the dynamic response of a model sand embankment(Doctoral Dissertation)[D]. Boulder: University of Colorado, 1989.

[11]Ilankatharan M. Centrifuge modeling for soil-pile-bridge system with numerical simulations accounting for soil-container-shaker interaction(Doctoral Dissertation)[D]. Davis: UC Davis, 2008.

[12]马军辉. 吊篮刚度对离心机振动台控制特性的影响[D]. 哈尔滨: 哈尔滨工业大学, 2011.