柱壳结构抗冲击性能量纲分析与数值模拟研究

赵 凯，高光发，王肖钧

(中国科学技术大学 近代力学系，合肥 230027)

柱壳是被广泛应用于大型油气存储工程，水下航行器，航空航天飞行器，各种杀伤性弹药武器的典型结构的代表，如何提高柱壳结构的抗冲击性能一直以来都是各国工程和防护领域科研工作者的重要研究课题。早期Rath等[1]基于薄壳理论研究了柱壳的振动问题，Qatu[2-3]提出了中厚复合壳的低阶近似振动方程，薄壁圆柱壳在动态和静态载荷下的失稳屈曲，一直以来都是学者们重点关注的课题[4-6]。近年来，Ebrahim等[7]采用各种三维剪切理论进一步研究了厚壳的静态和震动问题，Liu等[8]基于广义射线矩阵法和回传射线矩阵法研究了冲击载荷下层合柱壳的瞬态响应问题，Hu等[9]将薄壳理论和流固耦合方法RAVS相结合，提出了一种研究水中爆炸载荷下层合柱壳的瞬态响应计算近似方法，戴向胜等[10]用修正的Singace叠缩模型，研究了冲击载荷下含应变强化效应、应变率强化效应和温度效应的圆柱壳吸能情况。然而，这些理论方法毕竟具有一定的应用局限性。

在现代科学技术研究中，许多问题的解决都需要通过大量的实验才能实现。然而，实物的原型试验存在复杂性和难度很高、耗资巨大等种种问题，有时甚至是不可能实现的。因此在了解相应物理现象的基本规律的前提下，需要通过所谓模拟实验(或数值模拟)取得所研究问题中的一些基本规律和特征量，用于实物原型上。基于量纲分析中的相似律[11]，能让我们在模型研究中获得某种规律或特征量后，以无量纲特征量的方式直接用于原型，因此在学术研究和工程实践中都具有广泛的应用价值。本文以冲击载荷下柱壳的瞬态响应为背景，通过量纲分析研究了可简化为平面应变问题的柱壳在冲击载荷下的最大等效应力和最大等效应变所依赖的主要无量纲自变量，并开展相应的数值模拟，得到了不同相似比时的具体函数关系。

1 双层柱壳结构抗冲击性能的量纲分析

考虑冲击载荷作用下双层圆柱壳的瞬态响应问题。设给定一个长度为L、外半径为R的圆柱壳，壳体由两层不同材料组成(如图1(a)所示)。假设两层材料都满足各向同性理想塑性材料的Mises屈服准则。材料1壳环的厚度为H1，材料性能参数为ρ1(质量密度)、E1(杨氏模量)、ν1(泊松比)、Y1(简单拉压屈服应力)；材料2壳环的厚度为H2，材料性能参数为ρ2(质量密度)、E2(杨氏模量)、ν2(泊松比)、Y2(简单拉压屈服应力)。

壳体的任何响应量都是外载荷的空间分布和历时函数的泛函，我们考虑如下的外载：假设壳体在180°张角的外侧沿轴向均匀分布、而沿θ角按余弦规律分布的压力载荷p(t)cosθ的作用(如图1(b)所示)，载荷在θ=0°处的压力峰值峰值为p0、作用总时间为τ0、加卸载规律为三角形脉冲(如图1(c)所示)。

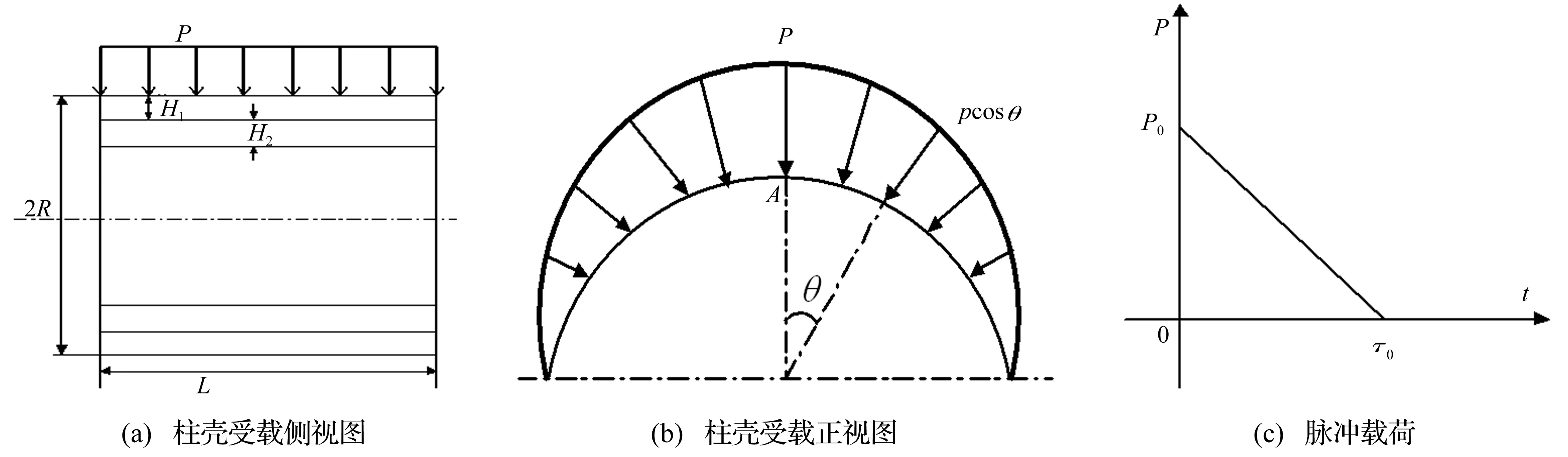
图1 柱壳上表面受均布载荷p的示意图

上述分布规律的外载荷作用下的柱壳的动力响应显然只依赖于载荷参数p0和τ0。考虑柱壳受载区域的中心点A处的最大Mises等效应力σmax和最大Mises等效应变εmax随外载的变化规律。如果柱壳材料是完全理想弹塑性材料，则我们可以确定如下一些物理量是问题的主定量(自变量)：柱体长度L、外径R、壳环厚H1和H2、材料性能参数ρ1,E1,ν1,Y1和ρ2,E2,ν2,Y2、外载荷参数p0和τ0，于是圆柱壳中任何点处(包括A点)的最大Mises等效应变εmax、最大Mises等效应力σmax应是这些物理量的函数，即

(1)

这里f(x)、g(x)表示某种函数关系。采用LMT单位制分析，式(1)中，因变量应变εmax本身已是无量纲量；L、R、H1、H2的量纲均是长度L；ρ1、ρ2表示材料的质量密度，其量纲可以表示为ML-3；因变量σmax和自变量E1、E2、Y1、Y2和p0都具有应力的量纲，可以表示为ML-1T-2；自变量ν1和ν2本身已是无量纲量；自变量τ0的量纲为时间T。

上述2个函数关系式在LMT单位制里，共有三个独立的量纲，可以取其中任何3个量纲彼此独立的物理量作为其基本量。我们将基本量组取为：圆柱壳体的半径R、材料1的质量密度ρ1和材料1的杨氏模量E1，因为这3个量是独立的、有较清晰的物理意义的量，且其它的因变量和自变量的量纲都可由它们的量纲表达出来。

(2)

在(2) 式中，对无量纲因变量起作用的无量纲自变量有11个：前3个是几何长度之比，即几何相似准数，它们反映了对结构几何尺度的几何相似要求；中间6个则是材料归一化力学性能参数，即材料相似准数，它们反映了对结构材料相似性的要求；倒数第2个表示以第一种材料的杨氏模量为基准而量度的外载荷归一化强度，即外载的动力学相似准数，它反映了对外载荷强度的动力相似要求；最后1个表示以第一种材料杆中弹性纵波波速传过结构特征尺度R所需时间为基准而量度的外载荷归一化历时。

函数关系(2)式的具体形式并不能单纯地由量纲分析方法而得出，而我们的任务就是通过实验、或者理论分析、或者模拟计算的方法确定上述多元函数的具体形式。

我们只讨论柱壳长度L足够大、而且整个壳的长度上都受有如上载荷的问题，则三维的柱体响应问题可以视为平面应变问题，此时L的大小将不影响柱壳中的归一化最大Mises等效应变和归一化最大Mises等效应力(严格而言当壳体的长度L为有限时还应引入壳两端的边界条件及相关的外载参数)。因此(2)式便简化为平面应变问题的动力响应问题，即

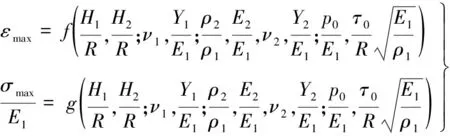
(3)

如果我们要用模型实验或者数值模拟的方法来寻求无量纲函数的具体形式，则必须保证模型问题(用下标m表述)和原型问题(用下标p表示)的完全物理相似，即

(εmax)m=(εmax)p,(σmax/E1)m=(σmax/E1)p

(4)

(5)

如果在下述条件下开展模拟实验或者进行模拟计算，可以进一步作如下简化：

①保持模型和原型满足几何相似条件，即

(6)

②假定模型和原型使用相同的材料，则自然就保证了材料相似，即有，

(7)

因而我们需要考虑的相似准数便只剩下外载荷的动力相似准数，此时(3)式可简化为

(8)

于是，在保证模型与原型几何相似和材料完全相同的前提下，我们要研究结构的响应规律(如某点的无量纲化最大Mises等效应力(σmax/E1)m和最大Mises等效应变值(εmax)m，只需通过模拟实验或者模拟计算的方法求出二元函数(8)式的相应数据，并通过拟合而求出这两个二元函数所表达的曲面就行了，也就是说，二元函数(8)式即柱壳最大等效应力和应变的具体依赖函数关系。

需要指出的是，虽然(8)式中没有显含材料的屈服强度Y，但是，无论对弹性材料还是对理想塑性材料，甚至不难证明对有硬化效应的弹塑性材料，在保持模型和原型几何相似及材料相似的前提下，上述问题的无量纲因变量与自变量的依赖关系都可由二元函数(8)所表达。对弹性材料和弹塑性材料进行模拟实验或模拟计算的时候，所得出的二元函数f或g的形式则必然是不同的，因为对弹性问题屈服应力Y不会发生作用，而对弹塑性问题要求材料进入屈服，所以屈服应力Y自然会发生作用。这里面隐含着另两个无量纲参数Y1/E1和Y2/E2的作用，但是在保持模型和原型材料完全一样的前提下，它们就是绝对常数，并不增加函数的复杂性，所以我们要寻求的仍然是二元函数。

2 双层柱壳结构抗冲击性能二元函数的数值模拟

采用国际商用冲击动力学软件LSDYNA，对上述问题进行数值模拟。柱壳外层材料是钢，内层材料是铝，采用线性硬化弹塑性本构模型，其基本力学参数如表1所示。柱壳的原型尺寸为，半径R=2 000 mm，H1=20 mm，H2=10 mm。原型上作用的脉冲载荷强度p0=500 MPa，τ0=20 μs。

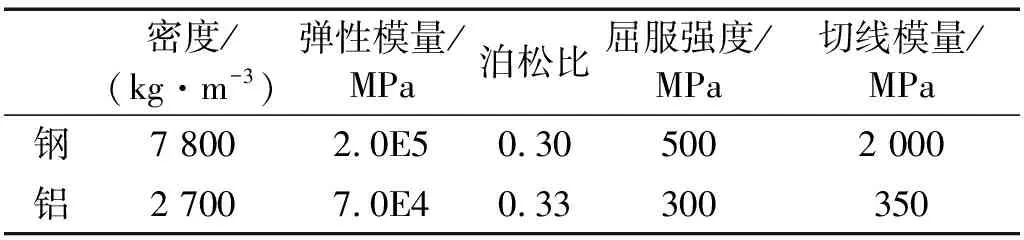
表1 材料基本力学性能

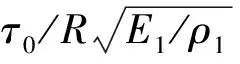
通过上述25个算例，可以得到不同半径、不同强度载荷下柱壳A点最大等效应力、最大应变的计算结果，如表2、表3所示。

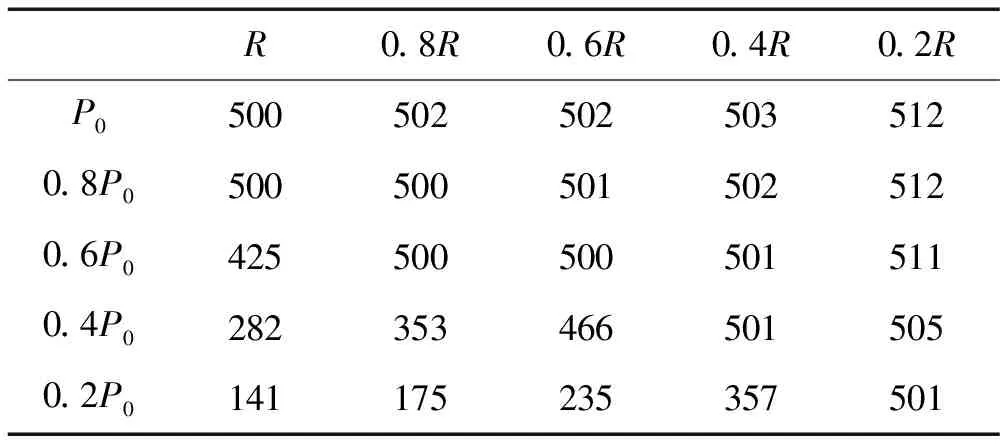
表2 A点最大等效应力(单位：MPa)

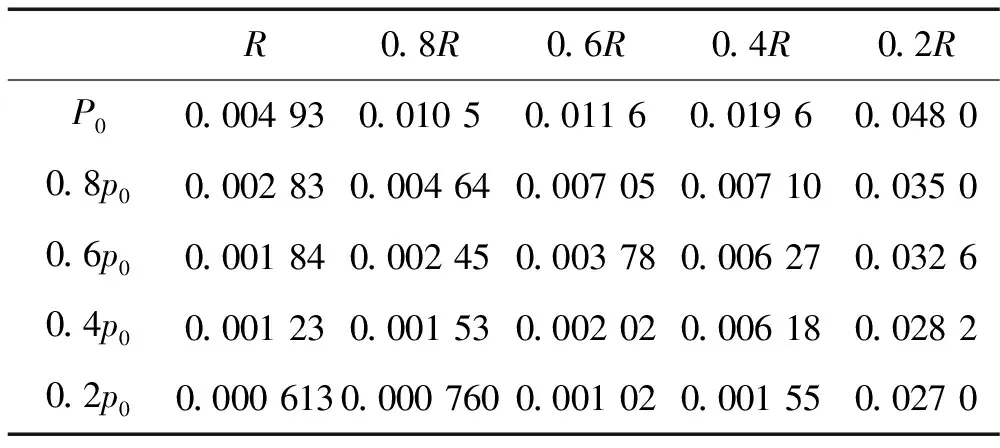
表3 A点最大等效应变

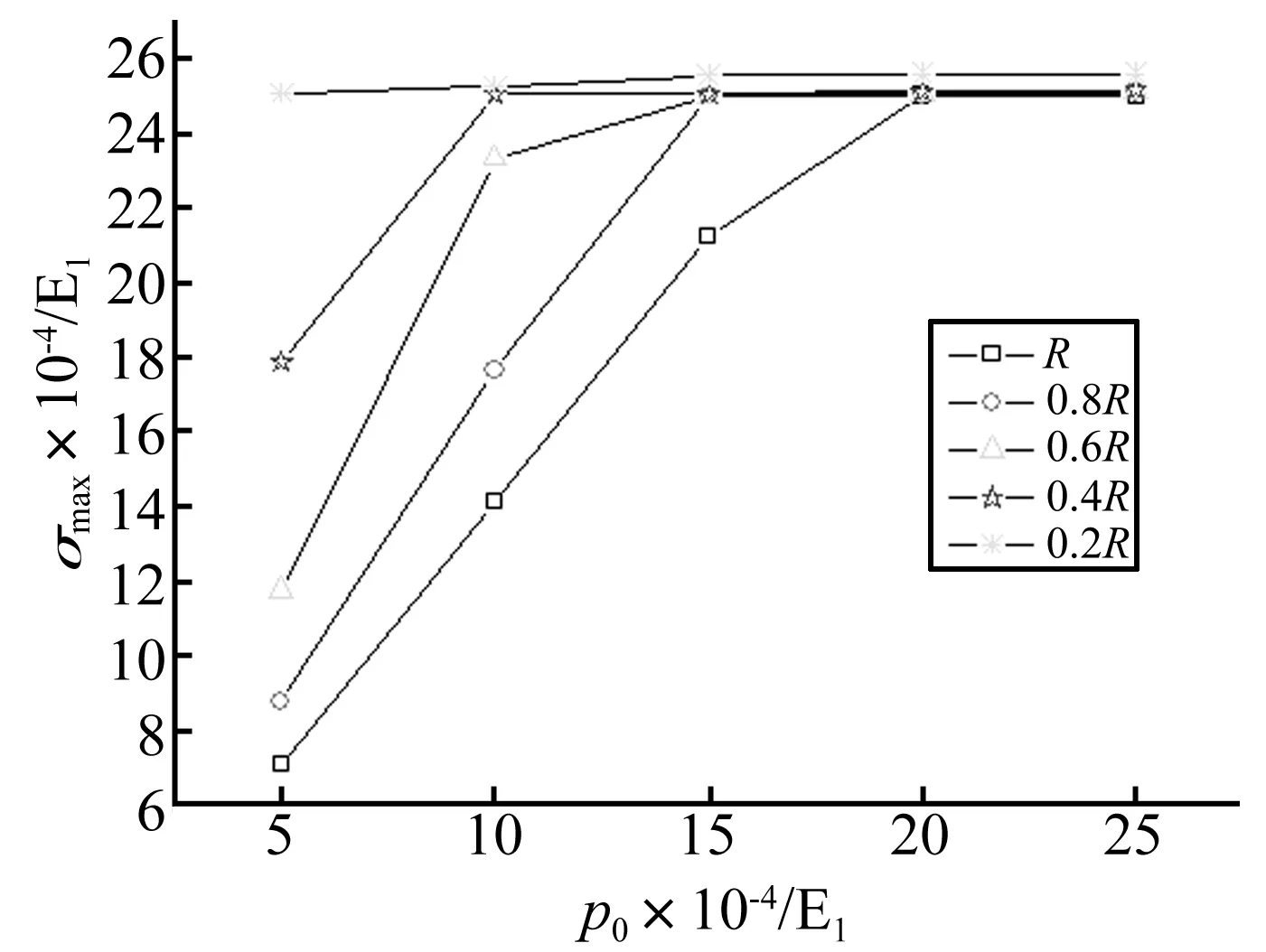
图2 σmax/E1 vs. p0 /E1

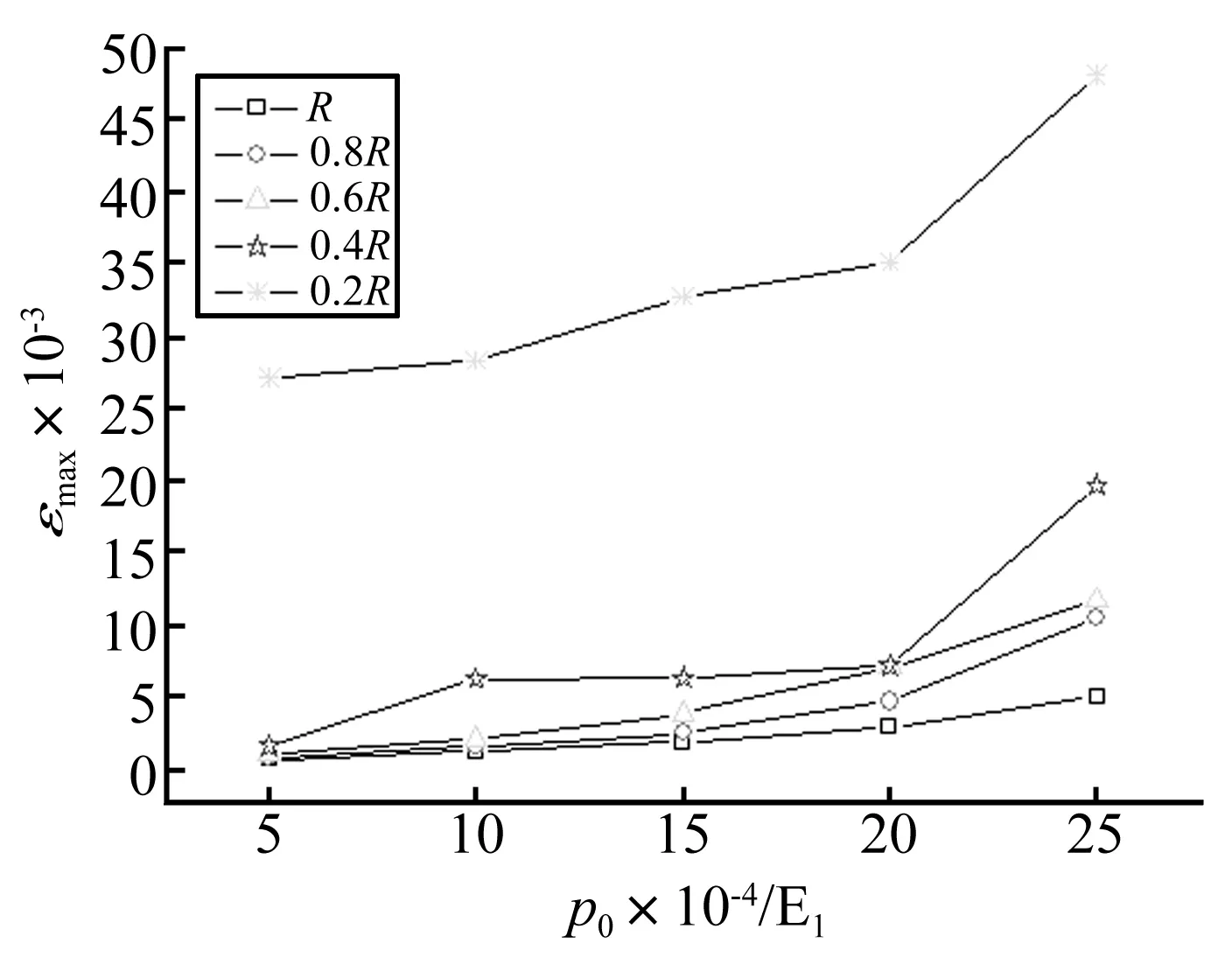
图3 εmax vs. p0 /E1

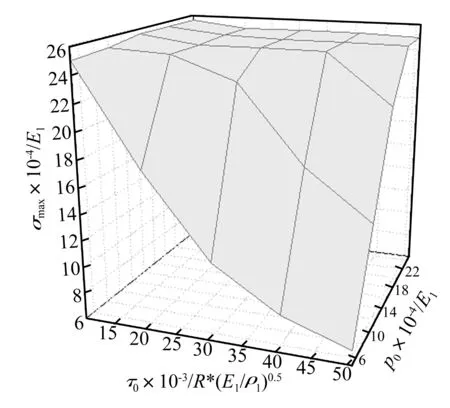
图4 无量纲最大等效应力函数曲面

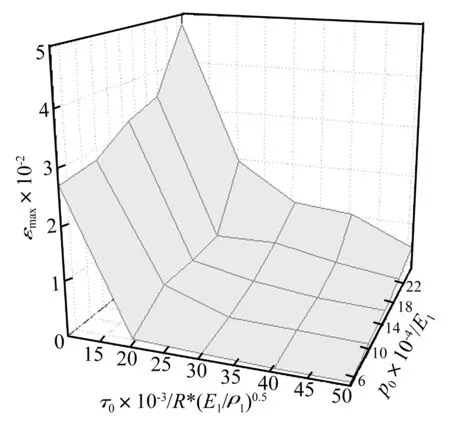
图5 无量纲最大等效应变函数曲面

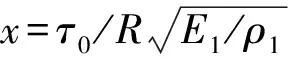
(9)

可得，a1=-2.540 45，b1=0.747 07，c1=35.233 81，d1=3 513.485 71，f1=-180.818 56，g1=0.045 62；a2=-0.050 28，b2=1.240 49，c2=-0.014 62，d2=-469.714 29，f2=22.848 68，g2=0.002 13。

3 结 论

以双层柱壳结构在脉冲载荷作用下的瞬态响应为例，通过量纲分析得出了可简化为平面应变问题的柱壳在冲击载荷下某点最大等效应力和等效应变无量纲因变量对主要无量纲自变量的函数依赖关系，并在模型和原型几何相似、所取材料相同的条件下，通过数值模拟得到了具体的二元函数表达，得出以下结论：

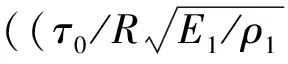
(2)数值模拟显示，在载荷强度不大、模型尺寸较大时，柱壳的最大等效应力和等效应变的无量纲函数呈线性，而随载荷强度的增大、模型的缩小，函数的非线性增长趋势显著。

[1]Rath B K, Das Y C. Vibration of layered shells[J]. Journal Sound and Vibration, 1973,28(4):737-757.

[2]Qatu M S. Accurate stress resultants equations for laminated composite deepthick shells[J]. Composites for the Pressure Vessel Industry, 1995(302):39-46.

[3]Qatu M S. Accurate equations for laminated composite deep thick shells[J]. Interational Jourmal of Solids and Structures,1999,36(19):2917-2941.

[4]Yamaki N．Elastic stability of circular cylindrical shell[M]．Amsterdam：North-Holland，1984．

[5]顾红军，赵国志，陆廷金，等.轴向冲击下薄壁圆柱壳的屈曲行为的实验研究[J].振动与冲击，2004,23(4):58-63.

GU Hong-jun,ZHAO Guo-zhi,LU Ting-jin,et al.Buckling of thin-wall cylindrical shell under axial impact[J].Journai of Vibration and Shock,2004,23(4):58-63.

[6]张善元，张涛.圆柱壳的轴向动力屈曲、参数共振与混沌运动[J].振动与冲击，2010,29(12)2:34-38.

ZHANG Shan-yuan,ZHANG Tao.Axial dynamic buckling,parametric resonance and chaotic motion of a closed cylindrical shell[J].Journai of Vibration and Shock,2010,29(12):34-38.

[7]Asadi E, Wang Wen-chao, Qatu M S. Static and vibration analyses of thick deep laminated cylindrical shells using 3D and various shear deformation theories[J]. Composite Structures, 2012,94(2): 494-500.

[8]LIU Chun-chuan, LI Feng-ming, HUANG Wen-hu. Transient wave propagation and early short time transient responses of laminated composite cylindrical shells[J]. Composite Structures, 2011,93(10): 2587-2597.

[9]HU Gang-yi, XIA Fei, LI Jun, The transient responses of two-layered cylindrical shells attacked by underwater explosive shock waves[J]. Composite Structures, 2010,92(7): 1551-1560.

[10]戴向胜,马建敏.冲击载荷作用下金属圆柱壳能量吸收研究[J].振动与冲击,2012,31(6):100-103.

DAI Xiang-sheng,MA Jian-min.Energy absorbed by a metal tube under axial crush load[J].Journal of Vibration and Shock,2012,31(6):110-103.

[11]谈庆明. 量纲分析[M]. 合肥：中国科学技术大学出版社, 2005.