可调控误报率和漏报率的树突状细胞算法＊

袁 嵩

（1.武汉科技大学计算机科学与技术学院，湖北 武汉430065；

2.智能信息处理与实时工业系统湖北省重点实验室，湖北 武汉430065）

1 引言

树突状细胞算法 DCA（Dendritic Cell Algo－rithm）［1］是受自然免疫系统中树突状细胞DC（Dendritic Cell）［2，3］的功能启发，对其抗原提呈行为进行抽象建模而衍生的人工免疫算法，已用于解决各类问题，特别是应用于异常检测领域［4，5］。DC的整个生物机制中存在着大量的生物要素，其中危险信号的融合及内部信号的生成是非常复杂的过程，至今仍有许多未知领域［6］。DCA是基于如此复杂生物机制的高度随机算法，涉及较多的相互作用成分和参数，所以难以对算法进行分析和控制。目前，对DCA的研究主要集中于提高检测精度和简化参数等方面［7，8］，针对 DCA参数敏感性分析和对检测结果灵活控制的研究还很少。

为了对检测结果误报率和漏报率进行有效的调控，本文从DCA权值矩阵对检测结果的影响入手，针对DC对细胞环境的评判准则提出倾向因子的概念，并将其融入到DC的状态转化机制中，设计一种改进的“投票制”DCA；作为投票制DCA设计思路的自然延伸，将DC对细胞环境的评判方式从投票改为打分，设计一个“评分制”DCA。本文给出了两种算法的设计思路和调控机制，并通过实验验证了算法的有效性和可控性。

2 传统DCA

DC在免疫过程中根据不同的生存环境呈现出三种不同的状态：未成熟状态、半成熟状态和成熟状态。DC被抽象为一个信号处理器，对输入信号进行融合处理得到输出信号来决定DC的状态，再根据DC的状态评价抗原的异常程度。其中，输入信号包括：病原体相关分子模式PAMP（Pathogen Associated Molecular Patterns）、危险信号 DS（Danger Signals）、安全信号SS（Safe Signals）、致炎细胞因子IC（Inflammatory Cytokines）；输出信号包括：协同刺激分子csm（co－stimulatory molecules）、半成熟树突状细胞因子semi（semi－mature DC cytokines）、成熟树突状细胞因子 mat（mature DC cytokines）。

DCA算法流程如下：

步骤1 DC摄取环境信号（PAMP、DS、SS、IC）和抗原。

步骤2 DC处理输入信号产生三种输出信号（csm、semi、mat）并分别进行累加。

步骤3 如果∑csm小于设定的迁移阈值MT（Migration Threshold）则继续进行步骤1和步骤2的操作；否则进行下一步。

步骤4 如果∑semi＞∑mat，DC转化为半成熟状态，抗原环境值标记为0；否则，DC转化为成熟状态，抗原环境值标记为1。

半成熟状态的抗原环境意味着抗原是在正常状态下收集的，而成熟环境则表示存在潜在的异常。通过计算每个抗原的成熟环境抗原值MCAV（Mature Context Antigen Value），即抗原被提呈为成熟环境抗原次数与被提呈的总次数的比值（反映抗原的异常程度），来检测是否存在异常。更多的算法细节参见文献［9，10］。

半成熟DC标记采样的所有抗原为正常，成熟DC标记采样的所有抗原为异常，这就好比DC作为评委，根据自身的状态为其采样的抗原投正常票或异常票，最后综合多个DC评判的结果得到抗原的异常程度。为此为每个抗原记下两个数据：投票总数和异常票数，当投票总数达到一个阈值N，计算该抗原的MCAV，即异常票数与投票总数的比值，再与异常阈值进行比较得到最终评价。本文把传统DCA称为投票制DCA，投票的准则即比较DC内累加的semi和mat浓度，是否公平取决于信号的融合处理机制。

3 信号的融合处理

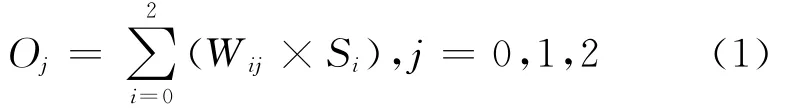
其中，Oj表示输出信号（O0～O2依次表示csm、semi、mat），Si表示输入信号（S0～S2依次表示PAMP、DS、SS），Wij表示从Si到Oj的权重。权值数据是由免疫学家通过对生物免疫的实验得出的，其中权值可以根据具体的应用场景进行调整，但是，输入、输出信号之间的相互影响关系应该满足：PAMP 影响csm、mat；DS 影响csm、mat；SS影响csm、semi和mat，并且SS对mat是负影响。目前常见的权值矩阵如表1～表3所示。

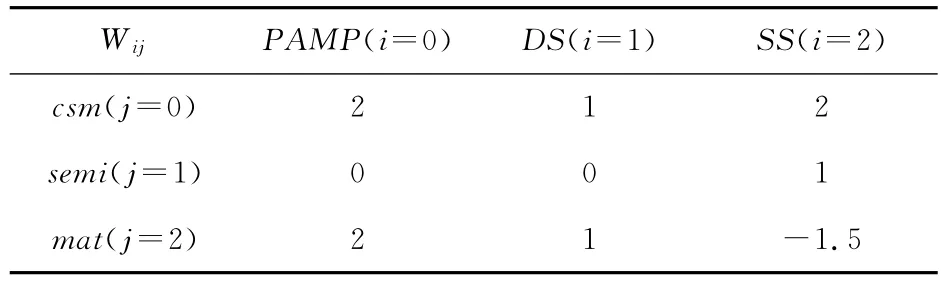
Table 1 Weight matric 1for DCA表1 DCA权值矩阵1

3.1 DCA信号转换处理公式和权值矩阵

信号的融合处理是非常复杂的过程，为了避免对复杂的实际生物信号转换机制进行建模，目前大多采用加权求和公式进行信号融合处理［11］。本文忽略了IC的影响，采用最简单的信号转换处理方式，如公式（1）所示，目的是为了更清晰地分析细胞环境转换的公平程度。

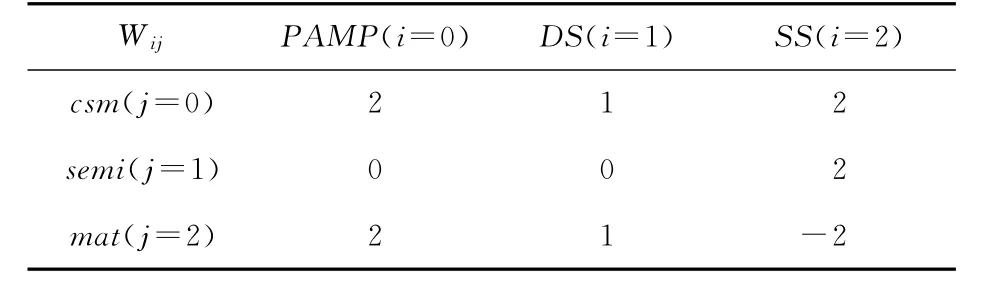
Table 2 Weight matric 2for DCA表2 DCA权值矩阵2

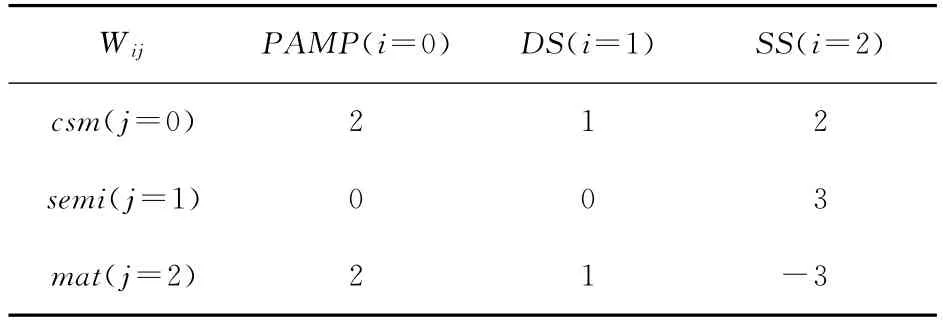
Table 3 Weight matric 3for DCA表3 DCA权值矩阵3

这三种权值矩阵的不同之处就在于SS对semi和mat的影响权重。

3.2 权值矩阵对检测结果的影响

本文选用文献［9］中提到的标准UCI Wisconsin Breast Cancer数据集，包括700条数据，其中240条标记为Class 1（正常），另外460条标记为Class 2（异常），数据的部分属性被抽象作为输入信号，将以上三种权值矩阵代入信号转换公式（1），并分别使用不同顺序的数据集进行实验：

（1）顺序1：前240条Class 1数据，后460条Class 2数据，让算法经历一次环境状态转换。

（2）顺序2：前230条 Class 2数据，中间240条Class 1数据，后230条Class 2数据，让算法经历两次环境状态转换。

（3）顺序3：115条Class 2数据＋120条 Class 1数据＋115条Class 2数据＋120条Class 1数据＋230条Class 2数据，让算法经历四次环境状态转换。

DCA是一个高度随机的算法，为了让实验结果具有可比性，所有参数设置相同，包括DC的迁移阈值也设置为一个固定值。但是，由于DC抗原采样的随机性，每种实验的每次结果仍不尽相同，表4是每种实验运行20次的平均精确度、误报率和漏报率。

表4中的实验数据反映出三种权值矩阵对检测结果的影响：权值矩阵1效果最好，检测精度最高，漏报率最低；权值矩阵3效果最差，虽然误报率最低，但漏报率最高；权值矩阵2效果居中。究其原因，正是这三种权值矩阵中SS对semi和mat的影响权重的不同导致了分类结果的差异。

以权值矩阵2为例，将700条数据的输入信号和权值矩阵2中的权重代入信号转换公式（1）可得到三种输出700组信号，分别求240个正常抗原的三种输出信号的平均值和460个异常抗原的三种输出信号的平均值，最后将这两组数据再求平均，本文称其为中性数据，如表5所示。

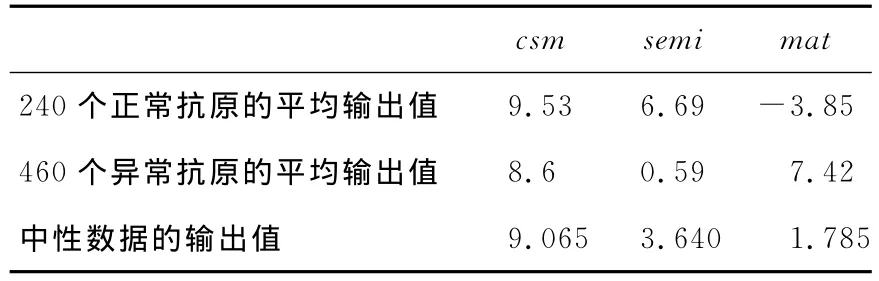
Table 5 Average output values of normal and abnormal antigens表5 正常、异常抗原的平均输出值

从表5可以看出，中性数据中semi＞mat，表明了DC对semi的倾向，也就是说，DC作为评委对于中性数据的评判偏向于安全，这也是导致最终漏报率偏高的原因所在。将中性数据的mat减去semi：1.785－3.640＝－1.855，该值表明了DC对semi的倾向程度，为此本文提出倾向因子的概念。

定义1 将输入信号和权值矩阵代入信号转换公式得到输出信号，分别求出正常抗原的三种输出信号的平均值和异常抗原的三种输出信号的平均值，将这两组数据再求平均得到中性数据的三个输出值，其mat与semi的差叫做倾向因子TF（Tendency Factor），反映了DC对安全或危险的倾向程度。

根据以上倾向因子的概念，将权值矩阵3代入信号转换公式（1），求得的倾向因子为－5.5，这说明DC对环境的判断更加偏向于安全，因此漏报率更高。将权值矩阵1代入信号转换公式（1），求得的倾向因子为＋0.87，这说明DC对环境的判断偏向于危险，因此漏报率低，并且该值最接近于0，说明DC对环境的评判较为公平。

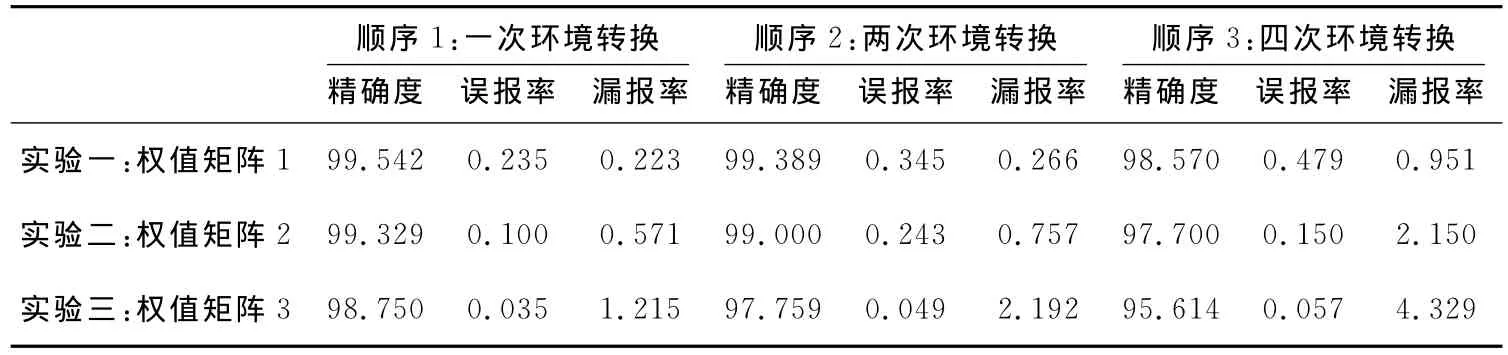
Table 4 Effects of weight matrixs on detection results表4 权值矩阵对检测结果的影响 %

由以上分析得出结论：不同的权值矩阵产生不同的倾向因子，反映了DC对安全或危险的倾向程度，随意的权值设置将导致DC对环境的盲目判断，因此传统DCA中DC的状态转换准则是有待改进的。

4 改进的投票制DCA

传统DCA中，当DC采样了足够的抗原达到迁移阈值时，通过比较∑mat和∑semi的大小来决定DC的转换状态存在一定局限性。因为通过不同的权值矩阵和不同的信号转换公式进行的信号融合处理得到的细胞环境评判具有不同的倾向程度。为了保证对细胞环境评判的公平，并可以灵活调控检测结果的误报率和漏报率，将倾向因子融入到DC状态转换机制中，改进DC状态转换准则，思路如下：

（1）数据集预处理，根据权值矩阵和信号转换公式求得倾向因子TF；

（2）初始化DC时增设一个变量n＝0，记载DC所采样的抗原个数，DC每采样1个抗原，该值加1；

（3）当DC内累加的csm达到迁移阈值时判断：如果∑mat－∑semi＞n＊TF，DC转化为成熟状态，否则DC转化为半成熟状态。

传统DCA中，DC状态转换的准则是判断∑mat与∑semi的差值是否大于0；改进的DC状态转换准则是判断∑mat与∑semi的差值是否大于n倍的倾向因子，其中，n指的是DC所采样的抗原个数。试想，如果DC采样一个抗原将引起一倍的TF倾向，若DC采样了n个抗原将引起n倍的TF倾向，用n＊TF作为标准来衡量∑mat与∑semi的差，目的是为了保证对环境是否安全或危险评判的公平。

采用改进的DC状态转换准则，重做以上三个实验，实验二和实验三取得了明显的改善效果，结果如表6所示。

由于实验一中求得的倾向因子为＋0.87，该值最接近于0，说明DC对环境的评判已经比较公平了，改进的实验效果并不明显，甚至稍逊于以前的实验效果，这说明融入倾向因子并非一定达到最优，但可作为寻求最优的参考。进一步的实验说明了这一点，表7为最优解的倾向因子调整范围。

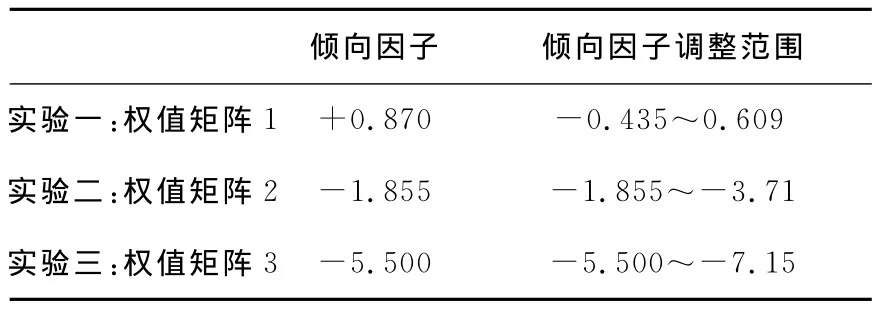
Table 7 Adjust range of TFfor optimal solution表7 最优解的倾向因子调整范围

更进一步，将（n＊TF）看作是安全或危险的临界值，设置一个稍大于（n＊TF）的值作为评判标准则偏向于安全，可适度降低误报率；反之设置一个稍小于（n＊TF）的值作为评判标准则偏向于危险，可适度降低漏报率。由此可以根据具体应用需求设置TF的值，调控检测结果的误报率和漏报率。

5 评分制DCA

5.1 算法思路

投票制DCA中，倾向因子的融入正是针对DC评判的公平准则，通过调整DC状态转换准则可控制异常检测的误报率和漏报率，但调控范围（如表7所示）是采用试探法通过大量实验得出的，并不直观，若能根据最后抗原的异常程度加以调控可获得更加直观的效果。因此，本节并不在DC状态转换机制上进行调控，而是忽略DC的状态转换，改投票制DCA为评分制DCA，具体思路如下：DC在抗原信号池采集信号和抗原，当DC内∑csm达到迁移阈值时，将∑mat与∑semi的差值当作分数评分给DC所采集的每一个抗原。为此为每一个抗原记下两个数据：评分次数和累计得分，当评分次数达到一个阈值N，计算该抗原的平均得分，即将累计得分／N作为抗原的MCAV，反映抗原的异常程度。也就是说，评分制DCA中DC不再为抗原投票，而是评分，也不存在DC的状态转换机制，最后根据得分情况确定分数线（即异常阈值）来调控检测结果的误报率和漏报率。

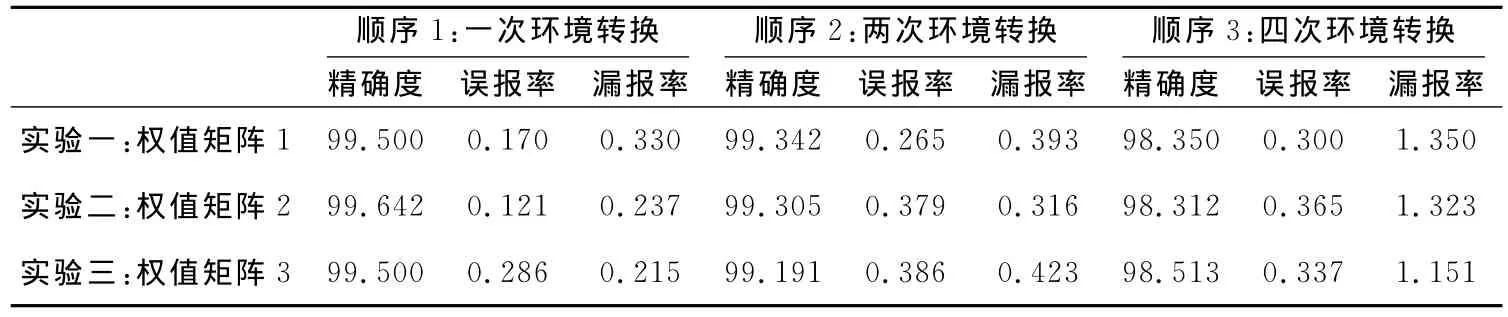
Table 6 Detecton results of the improved DC state transition rule表6 改进的DC状态转换准则的检测结果 %

5.2 评分制DCA的伪代码

输入：抗原和信号特征向量。

输出：每个抗原的平均分。

初始化一个长度为m的抗原信号池；

将数据集前m项数据放入池中；

while（抗原未全被检测完）

｛

初始化DC；

while（DC的∑csm＜迁移阈值MT）

｛

DC从抗原信号池中随机采样；

累计三个输出值：∑csm、∑semi、∑mat；

｝

对于DC采样的每一个抗原，评分次数加1，累计得分加上∑mat－∑semi的值；

处理评分次数达到N的抗原，平均分＝累计得分／

N，从抗原信号池中移除，加入新抗原；

｝

5.3 实验与结果分析

设置m＝20，N＝10，MT＝39，分别代入三种权值矩阵对顺序3数据集（115条异常数据＋120条正常数据＋115条异常数据＋120条正常数据＋230条异常数据）进行实验，效果如图1～图3所示，横坐标是700个抗原的ID，纵坐标是每个抗原的平均分。

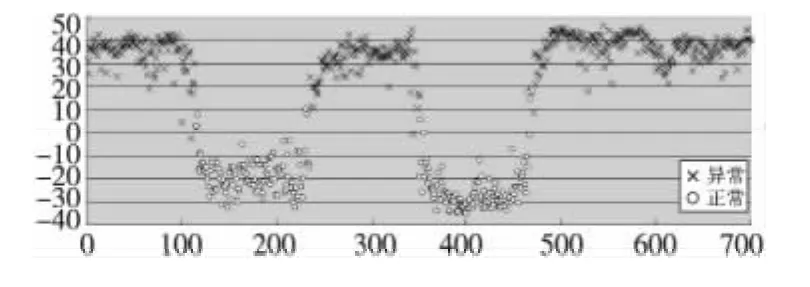
Figure 1 Experiment result using weight matrix 1of scoring DCA图1 评分制DCA代入权值矩阵1的实验结果

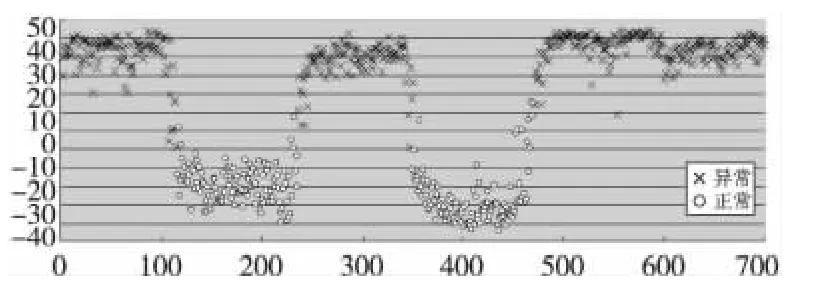
Figure 2 Experiment result using weight matrix 2of scoring DCA图2 评分制DCA代入权值矩阵2的实验结果

从三个实验的效果图可以看出：异常抗原的平均分主要分布在上部10～45，重心依次稍许下移；正常抗原的平均分主要分布在下部，重心依次明显

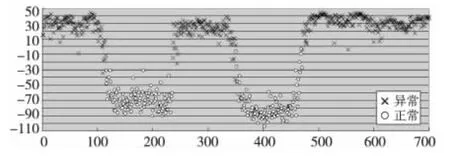
Figure 3 Experiment result using weight matrix 3of scoring DCA图3 评分制DCA代入权值矩阵3的实验结果

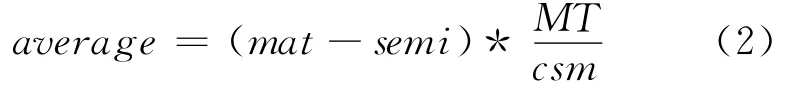
表5中的数据是以权值矩阵2代入信号转换公式（1）求得的正常、异常抗原的平均输出值，根据公式（2）可求得异常抗原的平均分约为（7.42－0.59）＊39／8.6＝30.97；正常抗原的平均分约为（－3.85－6.69）＊39／9.53＝－43.13。

另外，分别以权值矩阵1和权值矩阵3计算得到的平均分汇总如表8所示。下移。这是因为在危险环境中，SS一般为0，主要是PAMP和DS对输出信号产生影响，三种权值矩阵中PAMP和DS对输出信号的影响权值是一样的，所以对异常抗原的分值影响不大；在安全环境中，影响输出信号的主要因素是SS，三种权值矩阵的不同正是SS对semi和mat的影响权重，并且依次加大对semi的正影响和对mat的负影响，导致正常抗原的平均分重心依次明显下移。

根据抗原的平均输出值计算同种抗原的平均分的公式如下所示：

Table 8 Estimated values of average scores of normal and abnormal antigens表8 正常、异常抗原的平均分估算值

表8中的值是根据抗原的平均输出值计算得到的，实际抗原的分值会以此为基准上下波动，如图1～图3所示。

无论选用何种权值矩阵，都可将正常抗原和异常抗原划分开来，混乱均发生在两类环境交换的过渡阶段，这是由于DC在采样池中采样了多个抗原和多套信号，在转换边界两类数据的相互干扰所导致的。因此，只要根据正常抗原和异常抗原的分数分布选取合理的分数线（即异常阈值），便可灵活调控检测结果的误报率和漏报率。以图3为例：正常抗原的最高分为－2.737，异常抗原的最低分为－42.533，选取中间值－21.127作为异常阈值，可达到99%的检测精度，误报率为0.571%，漏报率为0.429%。异常阈值向上调至－2.737可实现0误报，向下调至－42.533可实现0漏报。当然这只是评分制DCA的一次实验结果，算法中大量的随机因素将导致不同的实验结果，每次实验的异常阈值上下值可调范围虽不尽相同，但中间值差异不大。

根据抗原的平均输出值计算中间值的公式如下：

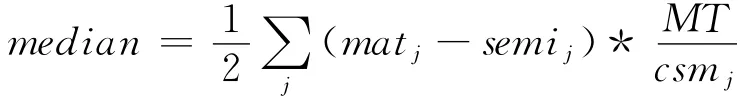
其中，j＝0，1，0表示正常，1表示异常。

中间值可作为异常阈值的参考值，然后根据具体应用调整异常阈值，可达到控制检测结果的误报率和漏报率的目的。

中间值也可表达为倾向因子的线性函数，融入倾向因子计算中间值的公式如下所示：

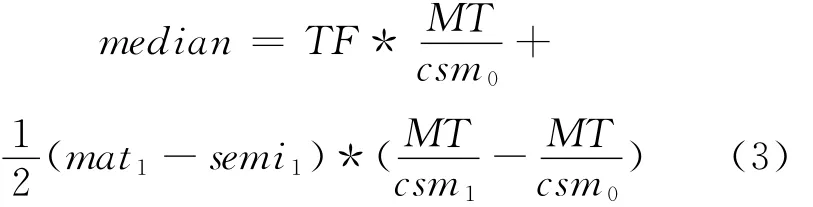
以权值矩阵2为例将表5中的数据代入公式（3）可得：

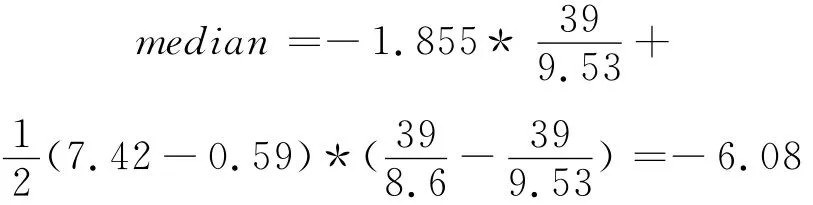
由于三种权值矩阵对异常抗原的影响并无太大差异，所以可将（mat1－semi1）当作一个常量，公式（3）可转化为：

median＝n＊TF＋t，n＝4.09，t≈1.55

如此代入三种权值矩阵的倾向因子，计算中间值分别为5.108、－6.037、－20.945，和表8中的中间值基本吻合。

6 结束语

本文从DCA权值矩阵对检测结果的影响入手，对信号的融合处理、DC的状态转化、抗原的综合评价等机制进行了分析，设计了两种可调控检测结果的DCA：改进的投票制DCA将DC的状态转换准则作为调控机制；评分制DCA通过分数线的合理划取调控误报率和漏报率。但是，这只是对DCA这种涉及较多相互作用成分和参数的高度随机算法进行分析和控制的初步研究，接下来的工作将继续深挖相关参数对检测结果的影响，进一步理解DCA的本质，并且根据检测结果进行反馈，动态调整参数，从而优化算法。

［1］ Greensmith J，Aickelin U，Twycross J.Articulation and clarification of the dendritic cell algorithm［C］∥Proc of the 5th International Conference on Artificial Immune Systems，2006：404－417.

［2］ Oates R，Kendall G，Garibaldi J.Frequency analysis for dendritic cell population tuning［J］.Evolutionary Intelligence，2009，1（2）：145－157.

［3］ Greensmith J，Aickelin U.Artificial dendritic cells：Multi－faceted perspectives［M］.Berlin：Springer－Verlog，2009.

［4］ Greensmith J，Aickelin U，Tedesco G.Information fusion for anomaly detection with the dendritic cell algorithm［J］.Information Fusion，2010，11（1）：21－34.

［5］ Twycross J.Integrated innate and adaptive artificial immune systems applied to process anomaly detection［D］.Nottingham：University of Nottingham，2007.

［6］ Ni Jian－cheng，Li Zhi－shu，Sun Ji－rong，et al.Research on differentiation model and application of dendritic cells in artificial immune system［J］.Acta Electronica Sinica，2008，36（11）：2210－2215.（in Chinese）

［7］ Yang Chen－xu，Wu Geng－feng，Hu Min.Improved dendritic cells algorithm［J］.Computer Engineering，2009，35（23）：194－200.（in Chinese）

［8］ Greensmith J，Aickelin U.The deterministic dendritic cell algorithm［C］∥Proc of the 7th International Conference on Artificial Immune Systems，2008：291－303.

［9］ Greensmith J.The dendritic cell algorithm［D］.Nottingham：University of Nottingham，2007.

［10］ Greensmith J，Aickelin U，Cayzer S.Detecting danger：The dendritic cell algorithm［M］∥Robust Intelligent Systems，London：Springer，2008：89－112.

［11］ Chen Yue－bing，Feng Chao，Zhang Quan，et al.Principles and application of dendritic cell algorithm［J］.Computer Engineering，2010，36（8）：173－176.（in Chinese）

附中文参考文献：

［6］ 倪建成，李志蜀，孙继荣，等.树突状细胞分化模型在人工免疫系统中的应用研究［J］.电子学报，2008，36（11）：2210－2215.

［7］ 杨晨旭，吴耿锋，胡珉.一种改进的树突状细胞算法［J］.计算机工程，2009，35（23）：194－200.

［11］ 陈岳兵，冯超，张权，等.树突状细胞算法原理及其应用［J］.计算机工程，2010，36（8）：173－176.