6自由度在刚体初始轨迹中的数值研究

杨 磊，肖天航

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室， 江苏 南京 210016)

6自由度在刚体初始轨迹中的数值研究

杨 磊，肖天航

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室， 江苏 南京 210016)

采用6自由度方法对刚体的运动姿态进行了仿真研究，通过求解刚体的动力学方程和运动学方程确定刚体的质心位置。在分析研究传统求解刚体欧拉角缺点的基础上，采用全角度转换的四元数法求解欧拉角，解决了非全角度转换的四元数法在大攻角情况下转换不准确的问题。对6自由度方法进行了算例验证，结果表明该方法正确、实用，与已有的模型相比具有更好的工程应用价值。

6自由度;欧拉角;四元数;角度转换;机弹分离

在研究物体(如飞行器外挂物、导弹等)6自由度运动姿态[1]时，本文引入“固化原理”，即忽略物体运动时的变形，这样物体的姿态可看作绕各个坐标轴的转动。物体的运动是关于时间的连续性问题，可以通过求解运动刚体的动力学方程和运动学方程确定其质心的运动轨迹。在对刚体运动姿态数值仿真中，一般采用的是方向余弦法和欧拉角法，但方向余弦法求解方程个数众多并涉及矩阵正交优化问题，求解难度大，耗时长；欧拉角法只有在攻角不大的情况下，才有较高的精度，在大攻角的情况下会出现奇点问题，求解结果会有很大偏差。因此需要研究人员研究新的方法描述刚体运动姿态角。

近年来，随着计算机[2]技术的飞速发展，以及航空航天、兵器等领域的需求，四元数法获得了广泛的应用，例如，载人飞船和航天飞机中的姿态控制、高性能飞机的空间机动、战术导弹对目标实施全方位攻击时采用的垂直发射技术等[3]。非全角度转换的四元数法在求解刚体运动姿态时虽然不会出现奇点问题，但因三角函数值域的局限会出现转换偏差。因此，本文采用全角度[4]转换四元数法求解刚体的欧拉角。

1 6 自由度模型的建立

1.1刚体质心运动轨迹方程

描述刚体质心运动轨迹通常采用惯性坐标系，其动力学方程为：

F=m·a

(1)

由于上述方程为矢量方程，所以将式(1)分解为沿三个坐标方向的方程组进行求解。应当注意的是有些量是惯性坐标系下的量(如重力等)，有些量是体坐标系下的量(如阻力、推力等)，这样就需要将体坐标系O-x1y1z1下的量转换成惯性坐标系O-xyz下的量，转换矩阵如下：

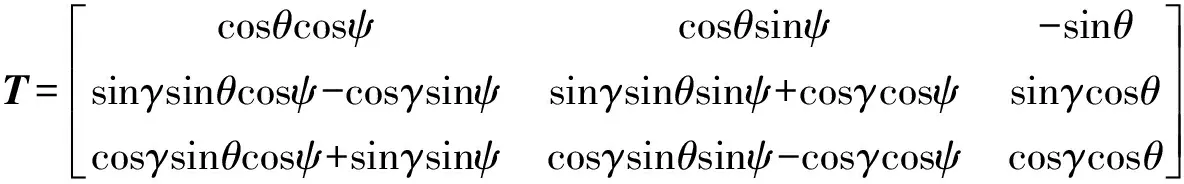
(2)

1.2刚体姿态角模型的建立

采用四元数[5]法可以确定刚体相对于全局坐标系的转动位置。在已知初始欧拉角的前提下，经过初始余弦矩阵可以求出初始四元数；给定时间步长Δt，通过求解四元数微分方程可求出下一步长的四元数值，再反求初始欧拉角到初始四元数的转换公式，最终可得到此时刻的欧拉角。在进行坐标转换时，本文规定按3-2-1的顺序转换。

a.初始欧拉角到初始四元数的转换。

(3)

通过式(3)就可以将初始欧拉角转换成初始四元数的值。

b.欧拉角和四元数的坐标变换矩阵。

无论是欧拉角的坐标变换还是四元数表示的坐标变换，只是同一变换的不同形式而已，所以这两种变换矩阵的对应元素相等，由此就可以用四元数来表示欧拉角。

四元数表示的坐标变换矩阵为：

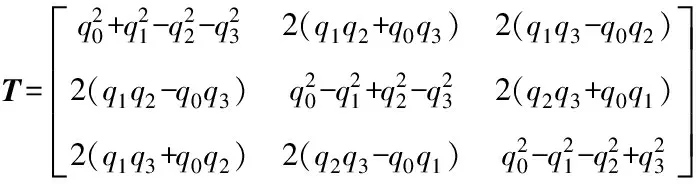
(4)

(5)

不难看出，式(5)只能表示3个轴在±90°范围的角度，又因为sin、tan函数在[-180°,+180°]范围内并不单调，不能准确地完成四元数和欧拉角之间的全角度转换，所以需要进一步讨论，其中T00～T33为坐标变换矩阵的元素。

当θ∈(-90°，+90°)，γ,ψ∈(-180°,+180°)时，四元数到欧拉角的转换公式为：

(6)

当θ∈(-180°，-90°)∪(+90°，+180°)，γ,ψ∈(-180°,+180°)时，四元数到欧拉角的转换公式为：

(7)

式(6)就是非全角度转换四元数法公式，也是目前广泛使用的一种方法。但俯仰角不能够实现全角度转换，所以本文结合式(7)提出全角度转换的四元数法，即θ，ψ，γ∈(-180°，+180°)。在已知(t+Δt)时刻的四元数的情况下，根据式(6)和式(7)可分别求出欧拉角A6(θ，ψ，γ)、A7(θ，ψ，γ)。因为本文仿真的数学模型是动态连续模型，欧拉角在Δt时间内的变化幅度比较小，不会发生角度突变，所以将欧拉角A6(θ，ψ，γ)、A7(θ，ψ，γ)分别与上一时刻的欧拉角At(θ，ψ，γ)比较，最接近的那个即为(t+Δt)时刻的大欧拉角At+Δt(θ，ψ，γ)。图1为四元数到欧拉角的全角度变换流程图。

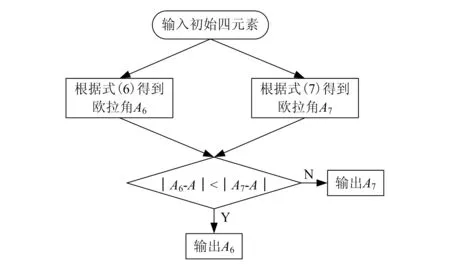
图1 四元数到欧拉角的全角度变换流程

2 四元数微分方程

通过求解四元数微分方程可以得到下一时间步长的欧拉角，但利用不同的坐标变换顺序得到的四元数微分方程也是不同的。本文以3-2-1的坐标变换顺序为例，其方程如下：

(8)

式中：ωx,ωy,ωz为刚体角速度在惯性坐标系上的分量。

3 刚体运动姿态的仿真分析

在数学模型建立后，利用计算机编程来模拟仿真，并得到0～15s的欧拉角曲线图。如图2所示，主要流程是：输入初始欧拉角、角速度和时间步长—计算机模拟仿真—输出下一时间步长时刻的欧拉角—输出欧拉角曲线图。在实例验证中，本文取(θ，ψ，γ)=(45°,60°,0°)，(ωx,ωy,ωz)=(0.1,0，0)，单位是(°)/s，仿真时间t=15s，并绘制0～15s内的曲线。

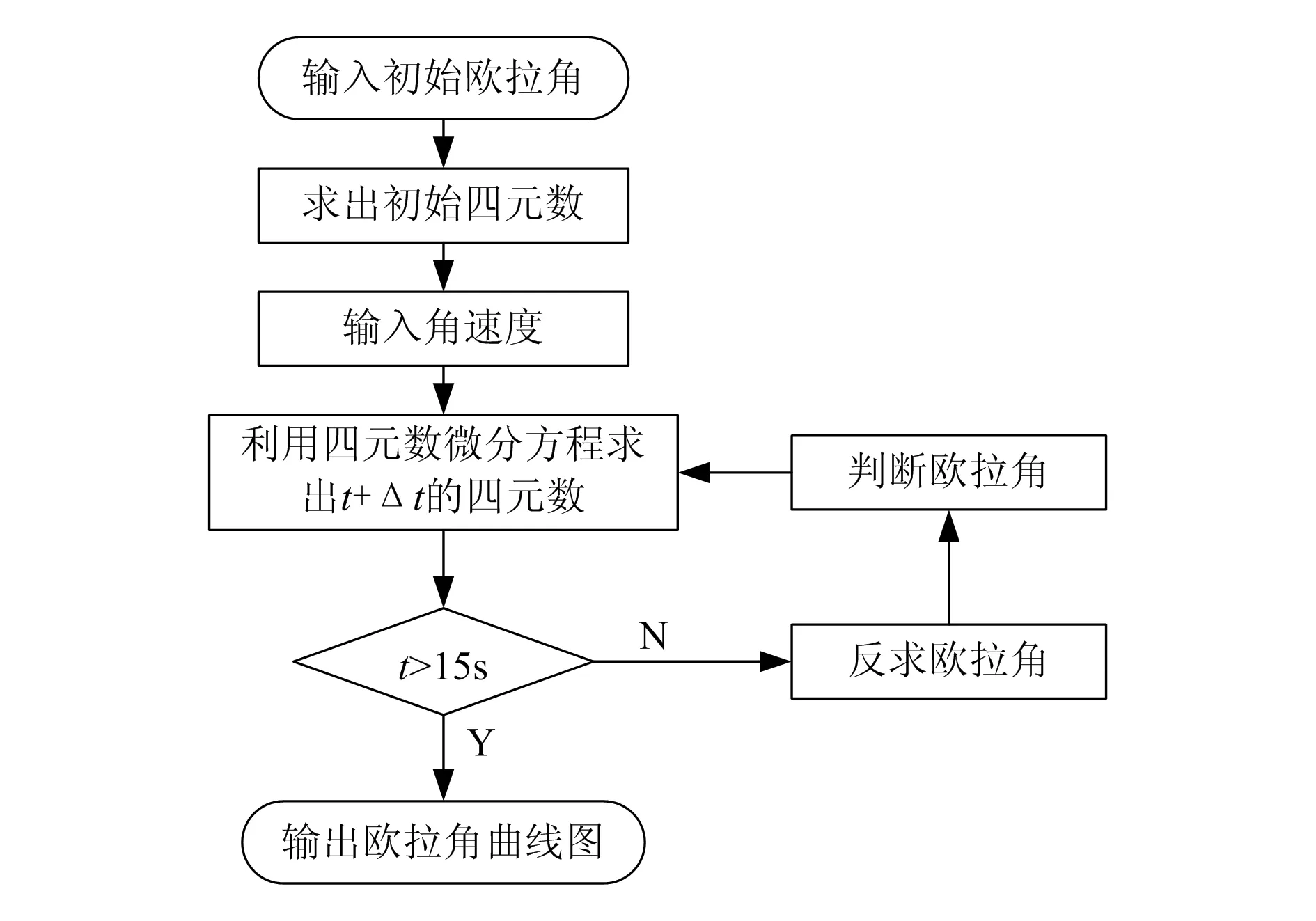
图2 计算机模拟流程

在初始条件一样的情况下，分别绘制成非全角度模型转换和全角度模型转换的曲线图。从图3和图4不难看出，在0～7.8s,两种方法模拟的欧拉角度完全一致；由于非全角度转换四元数法的取值范围θ∈(-90°,+90°)，因此当俯仰角超过其取值范围时，非全角度转换四元数法无法准确判断角度，从而出现了θ=90°时，ψ和γ的角度突变。从整个仿真时间段来看，θ角度的曲线出现尖点，随后欧拉角的转换发生错误。从全角度仿真曲线图中可以看出上述情况并没有出现，且较好地模拟了欧拉角的变化。

图3 非全角度转换的欧拉角曲线图

4 6-DOF算例验证

由于刚体质心位移模型只是确定刚体的位置，所以可以把刚体看作一质点。图5和图6分别是抛射角为0°、30°，抛射速度为1m/s，时间步长为0.100s，不考虑阻力情况下刚体的水平方向和垂直方向的位移图。通过和真实值比较，虽然有所偏差，但曲线符合度较好。

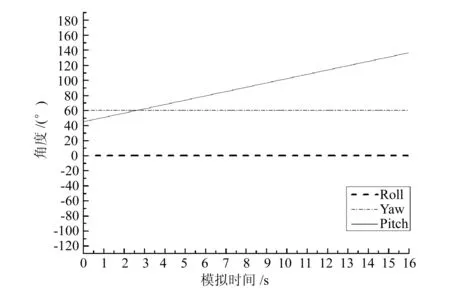
图4 全角度转换的欧拉角曲线图

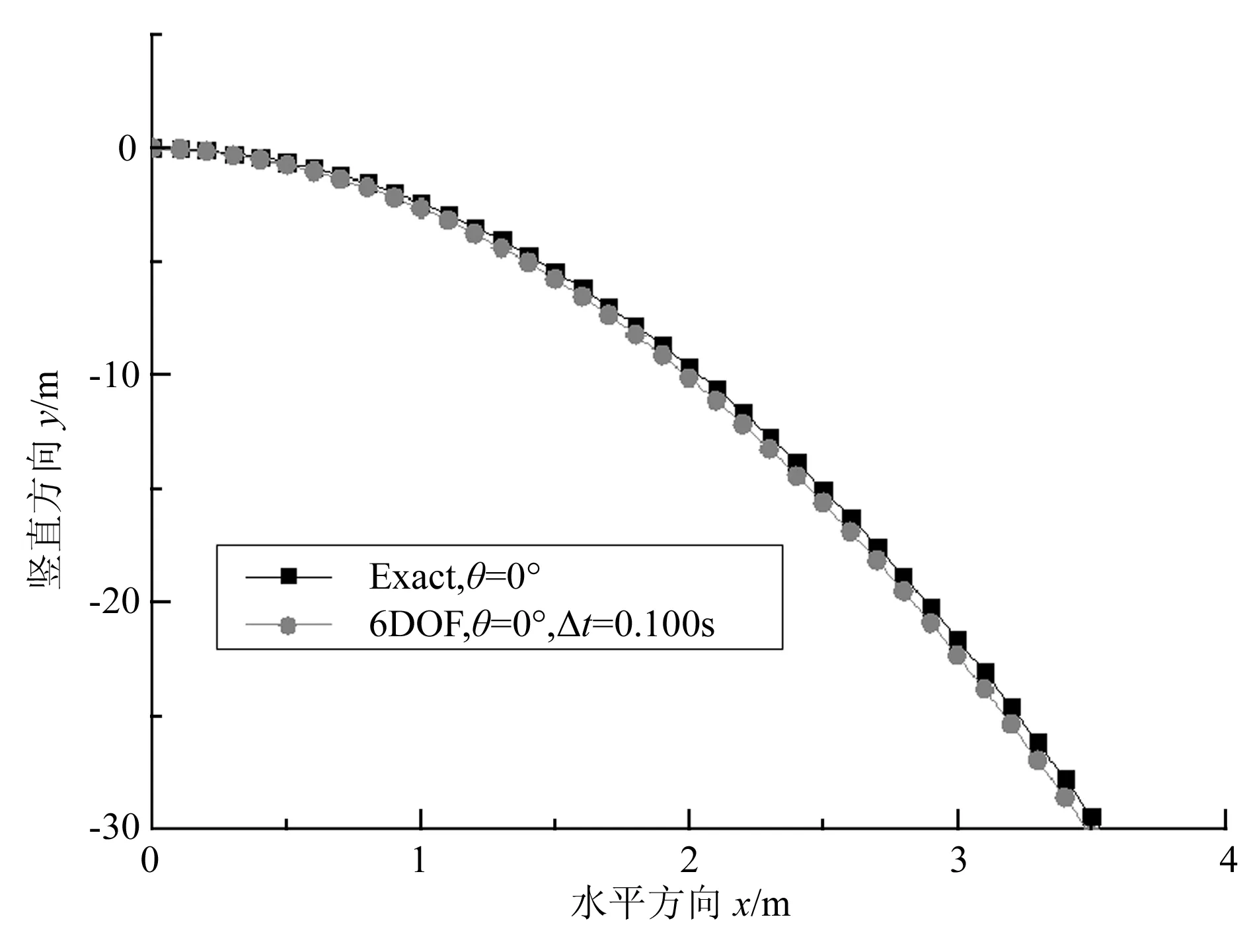
图5 抛射角为0°的质点位移图

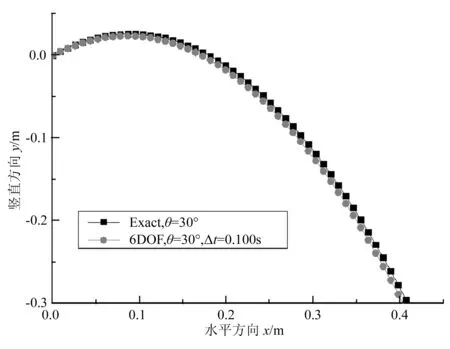
图6 抛射角为30°的质点位移图

为了研究时间步长和计算精度的关系，本文通过比较不同时间步长下的误差值发现，在其他条件不变的情况下，选择的时间步长越小，计算值与真实值的误差越小。图7是抛射角为-30°，抛射速度为1m/s，时间步长分别为0.001s、0.050s、0.100s，不考虑阻力情况下刚体的水平方向和垂直方向的位移图。若选取时间步长过大，由于时间的积累导致误差越来越大，最终会导致错误的发生；若时间步长选取很小，计算时间就会增加。在误差范围内，并有较快的计算速度，本文选取的时间步长为0.002s。

通过对二维平面内算例的验证，确定了时间步长，但是还不能够反映三维空间内质点的运动轨迹。本文对刚体质心位移模型进一步验证，分别给三个方向加力Fx=1N、Fy=5N、Fz=1N，重力大小为9.8N，x方向的速度为1m/s、其他两个方向速度均为0，时间步长为0.002s。图8为质点在三个方向力及重力作用下的空间轨迹图。

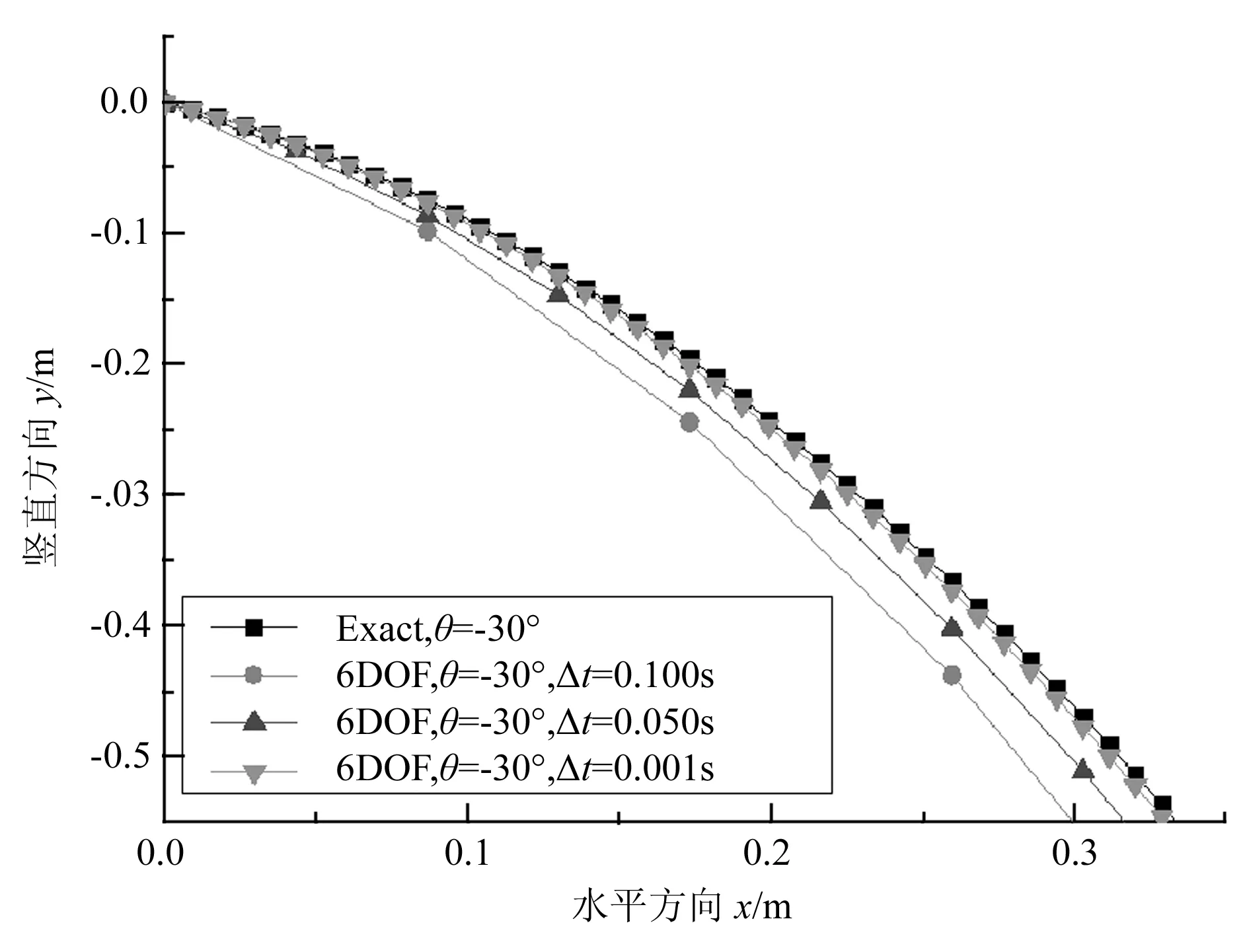
图7 不同的时间步长的质点位移图

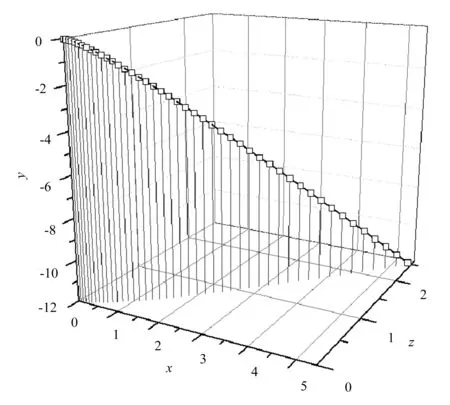
图8 三维空间内质点受力运动轨迹图

通过对二维和三维算例的分析，不仅证明了刚体质心位移模型的正确性，而且确定了求解运动方程的时间步长。

本文对刚体的姿态角模型进行了验证。该模型主要是为了描述刚体在受到外力矩的情况下，其姿态角绕质心的变化情况。假设刚体的质心坐标是(0，0，0)，在y轴方向加一对大小相等(Fy=20N)、方向相反、对质心的作用距离均为0.5m的力，作用时间1s。从图9可知,0～1s刚体在力的作用下加速度不断增加，当力矩消失后加速度保持不变；而z方向的欧拉角则做周期性的变化，如图10所示。

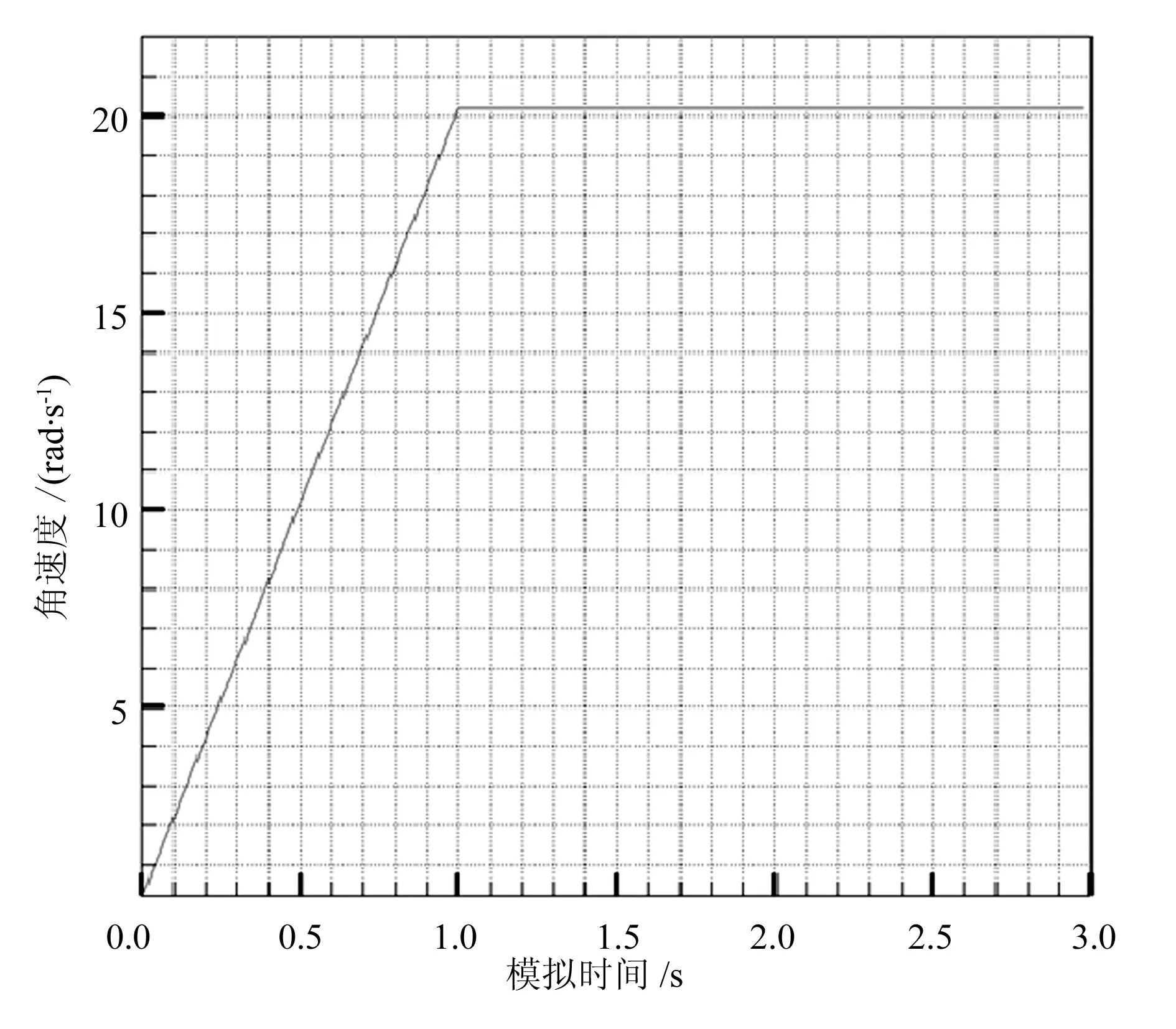
图9 绕z轴角速度的曲线图

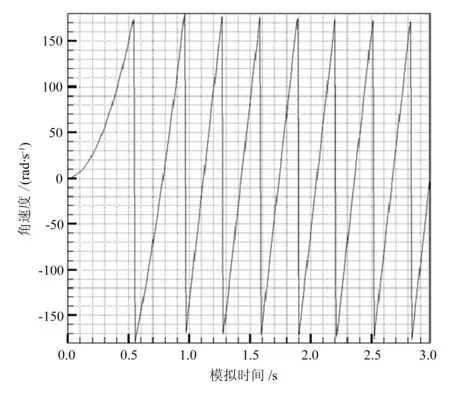
图10 绕z轴欧拉角的曲线图

5 结束语

本文对刚体的运动姿态进行了研究(包括刚体质心的位移和姿态角)。质心位移通过刚体运动学方程和动力学方程求得；本文主要创新点是通过与前一时刻角度信息的对比，修正了已有的四元数转换方法的角度局限，采用全角度转换四元数法对刚体姿态角进行了解算；采用四阶龙格-库塔法求解四元数微分方程，将求得的四元数进行归一化处理，降低了计算机浮点误差对结果的干扰，提高了精确度。本文提出的新型仿真模型对飞行器和卫星的姿态描述有重要意义。

[1] 钟山.基于机器学习的卫星姿态控制律设计[J].航天控制，2011(8)：82-85.

[2] 王夙娟.卫星的姿态控制研究[J].电子技术，2012(6)：120-121.

[3] 李轶.一种卫星姿态轨道确定系统及方法[M].北京：北京航空航天大学，2012.

[4] 张帆.一种新的全角度四元数与欧拉角的转换算法[J].南京理工大学学报，2002(6)：20-23.

ARigidBodyNumericalSimulationBasedonSixDegreesofFreedomMethod

YANG Lei, XIAO Tianhang

(Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China)

It introduces the simulation of rigid body motion attitude with six degrees of freedom method. In order to determine the CG position of the rigid body, it solves the equation of rigid body dynamics and kinematics equations. Based on the shortcomings analysis of traditional methods and comparing with non-point conversion quaternion method, it shows that the proposed method can avoid the problem of inaccurate conversion for solving speed and angle of attack. The results prove that this method is correct and practical, and has better value in engineering applications than the existing other methods.

Six-DOF; Euler Angle; Quaternion; Angle Conversion; Wing-Store Separation

10.3969/j.issn.2095-509X.2014.03.002

2013-11-29

航空科学基金资助项目(20100152002);江苏高校优势学科建设工程资助项目

杨磊(1988—)，男，江苏南通人，南京航空航天大学硕士研究生，主要研究方向为飞行器总体设计。

V211.3

A

2095-509X(2014)03-0005-05