留数计算方法的研究与推广

沈 霞

(九江学院理学院 江西九江 332005)

留数计算方法的研究与推广

沈 霞

(九江学院理学院 江西九江 332005)

作者在传统留数计算方法的基础上，研究并推广了留数计算方法，解决了一类函数的留数计算问题.

留数，极点，零点

留数(残数)是复变函数中的一个非常重要的概念，它在积分计算、辐角原理、拉氏变换等问题中都起到很重要的作用.关于函数在极点处的留数，文献[1]中给出了如下计算方法：

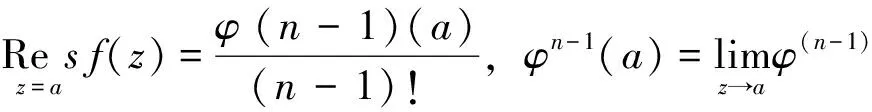
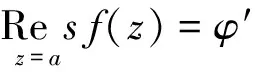
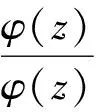
本文将上述定理做适当推广，并给出一般性结论.

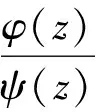
证：因为z=a为φ(z)的n阶零点，为ψ(z)的n+1阶零点，故由解析函数的展开定理知：

φ(z)=φn·(z-a)n+φ(n+1)·(z-a)n+1+…=(z-a)n[φn+φn+1·(z-a)+…]=(z-a)nP(z)，

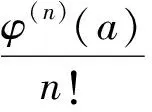
ψ(z)=ψ(n+1)·(z-a)n+1+ψn+2·(z-a)n+2+…=(z-a)n+1[ψn+1+ψn+2·(z-a)+…]=(z-a)n+1Q(z)，

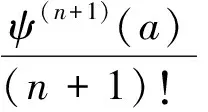
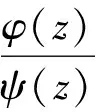
推论1 当定理1中的n=0,λ=0时，定理1的结论便为文献[1]中定理B的结论.

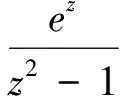
解：z=1为f(z)的一阶极点，由定理1知(n=0,λ=1,a=1,φ(z)=ez,ψ(z)=z2-1)

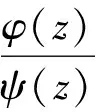
证：由题设及定理1的证明过程知：

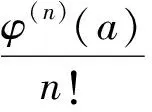
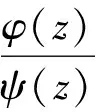
解：z=i为f(z)的二阶极点，由定理2知(n=0,λ=i,a=i,φ(z)=eiz,ψ(z)=z(z2+1)2)

[1]钟玉泉.复变函数论(第4版)[M].北京：高等教育出版社，2013.221.

[2]龚冬保.复变函数典型题[M].西安：西安交通大学出版社，2002.281.

(责任编辑李佳瑜)

2014-9-30

沈霞，shenxiawan@163.com。

O 174.5

A

1674-9545(2014)04-0055-(02)