反向旋转双转子系统加速响应特性研究

杨喜关， 罗贵火， 王 飞， 唐振寰

(南京航空航天大学 能源与动力学院，南京 210016)

对航空发动机高性能、高可靠性的追求，使反向旋转双转子技术与中介支承技术得以应用，但却使转子系统动力特性更复杂；而双转子系统需要在短时间内实现某种转速变化，其瞬态响应特性与单转子瞬态响应特性有一定区别。因此，研究反向旋转双转子系统瞬态运动对掌握含中介支承转子系统的动力特性、判断转子系统工作状态具有实际应用价值。以往对双转子系统瞬态响应特性研究，多集中于突加不平衡量的瞬态响应特性研究[1-5]；近来已有对双转子系统在碰摩、支承非线性力作用下的双转子系统非线性动力特性研究[6-8]。而关于反向旋转双转子系统的研究报道较少。国外对反向旋转双转子系统动力特性进行的相关研究[9-11]多集中于线性领域。国内冯国权等[12-13]先后对反向旋转双转子系统的临界转速与不平衡响应计算进行分析；胡绚等[14]采用传递矩阵法分析具有中介轴承的反向旋转双转子结构稳态响应分析及试验研究。自此，关于变速过程中反向旋转双转子系统瞬态动力特性研究鲜有报道。

本文以含中介支承的五支点双转子系统为研究对象，借助有限元软件与模态综合法建立转子系统的动力学模型，研究反向旋转双转子系统在均匀加速过程中的瞬态响应特性，并对部分结果进行试验验证。

1 双转子系统建模及降维方法

1.1 双转子系统模型

图1 五支点双转子系统结构简图

据现有航空发动机中五点支承结构的双转子系统结构特点，设计双转子试验器，图1为五支点双转子系统试验器结构简图。内、外转子通过中介支承Ⅳ连接，且以一定转速比运转，运行中仅转子盘处存在不平衡作用力；忽略转子系统外部阻尼、材料阻尼，考虑各圆盘处陀螺力矩；为直观展现转子在变速过程中的转子动力特性，将各支承简化为线性刚度及阻尼。

1.2 双转子系统动力学模型建立

对转子系统进行子结构划分，释放各支承处约束，得内、外转子两子结构A，B。在有限元分析软件中，建立子结构有限元模型，提取子结构质量矩阵Ml及刚度矩阵Kl，设子结构节点个数为nl。则子结构运动方程可写为：

(1)

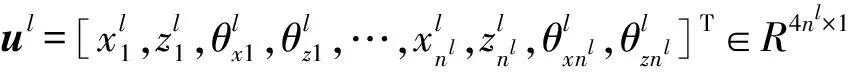
设子结构转子系统转速为ΩL，则子结构陀螺矩阵可写为：

(2)

式中：

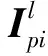
匀变速子结构不平衡力向量为：

(3)

式中：

用J表示子结构模型中界面物理自由度全体，I表示内部自由度全体，则式(1)可写为：

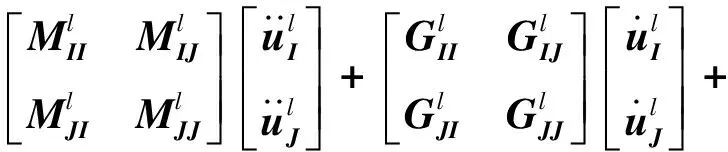
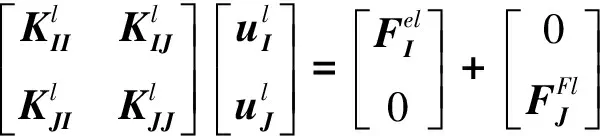
(4)

对接界面作用力向量为：

(5)

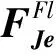
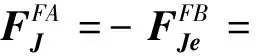
(6)

式中：kAB，cAB为中介支承处刚度、阻尼矩阵。则非中介对接界面作用力可写为：

(7)

式中：kl，cl分别为非中介支承处刚度、阻尼矩阵。

1.3 模型降维

采用固定界面模态综合对双转子系统进行自由度降维。对固定界面子结构而言，子结构坐标变换模态由两组模态组成：① 固定界面子结构主模态；② 约束模态。物理坐标与模态坐标变换关系为：

(8)

(9)

将式(8)代入式(2)，并两端前乘TlT，则有：

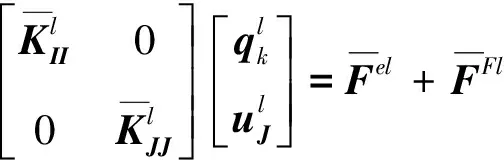
(10)

式中：

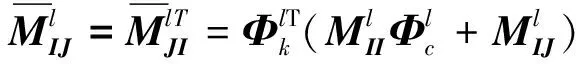
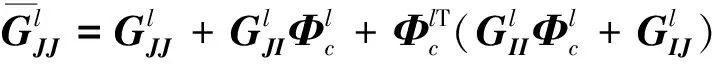
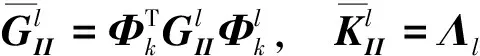
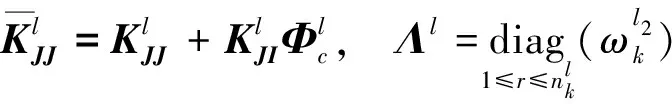
对各子结构进行组装，得整个双转子系统模态空间中运动方程为：

(11)

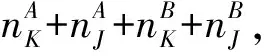
2 反向旋转双转子系统加速响应特性分析

2.1 转子系统模型建立

图2为双转子试验台结构简图，在ANSYS中，采用基于Timoshenko梁理论的3节点单元BEAM189及mass22号单元，分别建立该试验台的内外转子轴及转子盘有限元模型，并提取内外转子质量矩阵、刚度矩阵。有限元模型中内转子节点个数为301，外转子节点个数为177；利用固定界面模态综合法对系统进行缩减，通过ANSYS软件计算内外转子前15、前10阶模态参数。

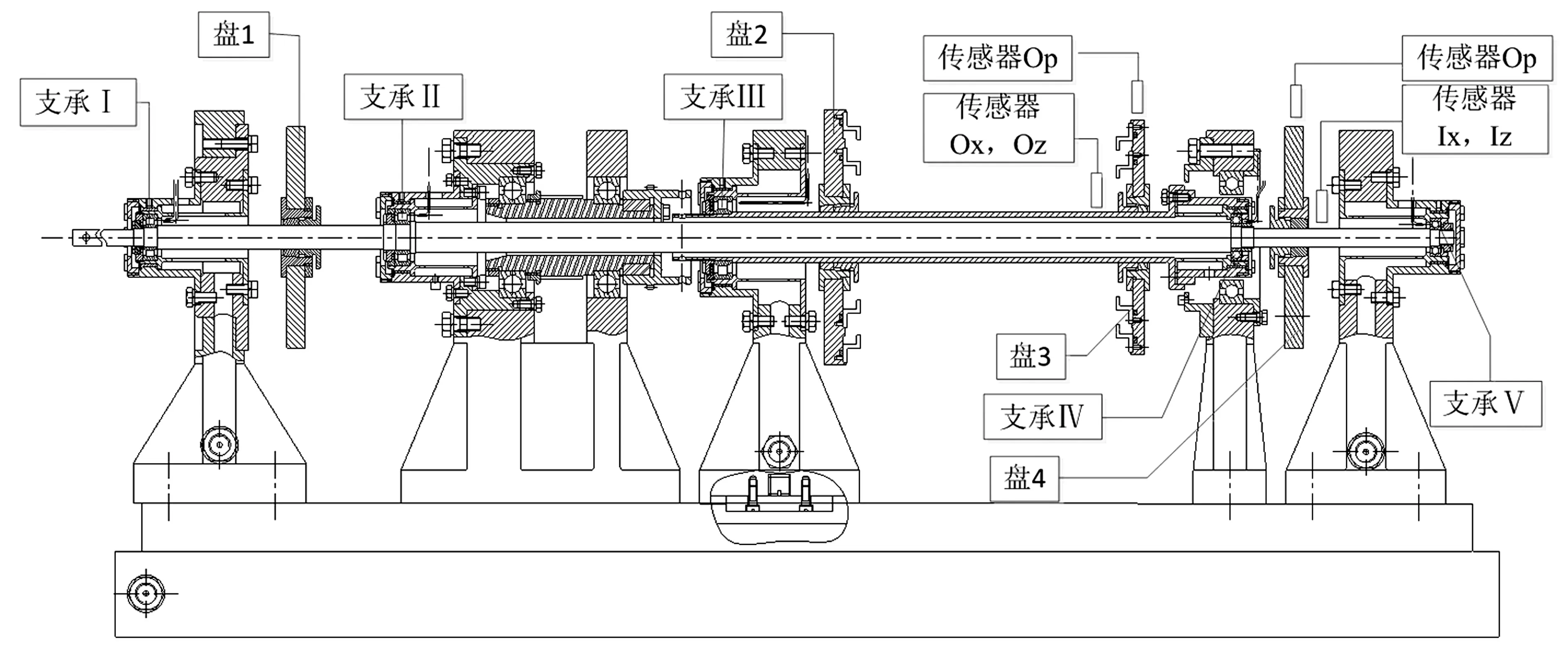
图2 试验台示意图

各支承处刚度、阻尼值见表1，各轮盘偏心距均取1×10-4m。该结构临界转速见表2，对应的振型见图3～图5，图中竖直线“|”表示支承位置,“*”表示圆盘位置。

图3 反向旋转双转子系统第一阶振型

图4 反向旋转双转子系统第二阶振型

表1 支承刚度值选取

表2 反向旋转双转子临界转速

图5 反向旋转双转子系统第三阶振型

2.2 计算结果分析

双转子系统的等加速瞬态响应与等减速瞬态响应响应特性近似，限于篇幅本文仅对双转子系统加速响应特性进行分析。

转子系统等加速越过临界转速时，出现瞬态响应的峰值转速会滞后临界转速，且加速度值越大，瞬态响应峰值越小，响应特性不明显；加速度值越小，瞬态响应峰值越大，危害试验台安全。为直观分析该系统加速响应特性，并考虑试验台性能，计算中取内转子从转速10 rad/s以恒定加速度10π rad/s2稳定加速到500 rad/s，内外转子转速比取1.6。

2.2.1 转子振型对双转子系统瞬态加速响应影响

内外转子转速在恒定加速度下随时间变化规律见图6，双转子系统各截面处时域响应见图7。图7中响应峰值对应的转子转速均可在表2中找到对应的临界转速，但均滞后临界转速一定时间间隔，与单转子加速过程特性相同。表2中转子临界转速却不能在图7中找到对应关系。各圆盘处转子振动时域图存在一定差异：即振动幅值大小不同，振动峰值出现位置亦不同。此现象与转子各阶振型有密切联系。

由图3与图7对比可知，一阶临界转速时内外转子均参与振动，内外转子出现较强的耦合振动；盘1～盘4的瞬态加速响应中均出现内、外转子为主激励一阶临界转速引起的振动峰值，且在中介支承附近振幅较大，见图7(c)、(d)，与图3中一阶临界振型有较好对应关系。

由图4、图7对比，分析二阶临界振型对时域图影响，即图4二阶振型中，仅盘1处振幅相对较大，外转子基本不参与振动；图7中，盘2～盘4加速瞬态响应图中均未出现明显二阶临界转速对应的振动峰值，但盘1瞬态响应图中有与二阶临界转速对应的振动峰值。

由图5、图7对应关系分析三阶振型与加速瞬态响应关系，即盘2处振幅较大，在盘2瞬态响应图中反应明显；其它各盘处虽参与振动，但振幅相对较小，见图7(a)、(c)、(d)。

以上分析看出：对特定结构的双转子系统，特定截面处瞬态加速响应并不会出现对应所有临界转速的振动峰值，其瞬态响应特性与各界临界转速与振型有密切联系，且转子不同截面处的瞬态响应特性亦存在一定差异。

图6 转子转速随时间变化

2.2.2 转子加速过程中各转子进动转速变化规律

以盘3、盘4为例分析转子瞬态加速响应规律。转子系统加速过程中各转子进动速度随自转速度变化规律见图8。由图8看出，外转子为主激励的一阶临界转速前，内、外转子进动速度均围绕外转子转速附近上下跳动，转速增加到外转子为主激励的一阶临界转速附近时，转子公转速度上下跳动幅值最小。在两个一阶临界转速之间时，转子公转速度幅值跳动剧烈，期间某一转速处，内转子由非协调反进动变为非协调正进动，外转子由非协调正进动变为非协调反进动，随后转子公转速度上下跳动幅值逐渐减小，在内转子为主激励的一阶临界转速附近达最小值。加速过程中变化规律近似，不再赘述。

可见，反向旋转双转子系统由某阶临界转速向下一阶临界转速变化过程中，转子公转转速存在剧烈变化过程，转子处于较强烈非协调进动状态。

2.2.3 转子加速过程中各转子质心变化规律

图9、图10分别为内外转子盘质心相位角随旋转速度变化趋势。由图9看出，初始转速开始，盘3质心相位角波动均值呈上升趋势，在外转子为主激励的一阶临界转速处，其波动均值达π/2,随转速的增加，其质心相位角波动均值达π，完成外转子质心换向，在随后一段时间内，盘3质心相位角围绕 π上下波动，波动幅值呈放大趋势，在达到外转子为主激励的下一阶临界转速前，盘3质心相位角逐渐增大，随后重复质心换向过程。由图10看出，初始转速开始，盘4质心相位角逐渐增大，在包括内转子为主激励的一阶临界转速某一转速范围内盘4完成质心换向过程，达到内转子为主激励的下一阶临界转速前，盘3质心相位角逐渐增大，随后重复质心换向过程。

以上分析可知，内外转子质心换向过程分别出现在以各自为主激励的临界转速附近。

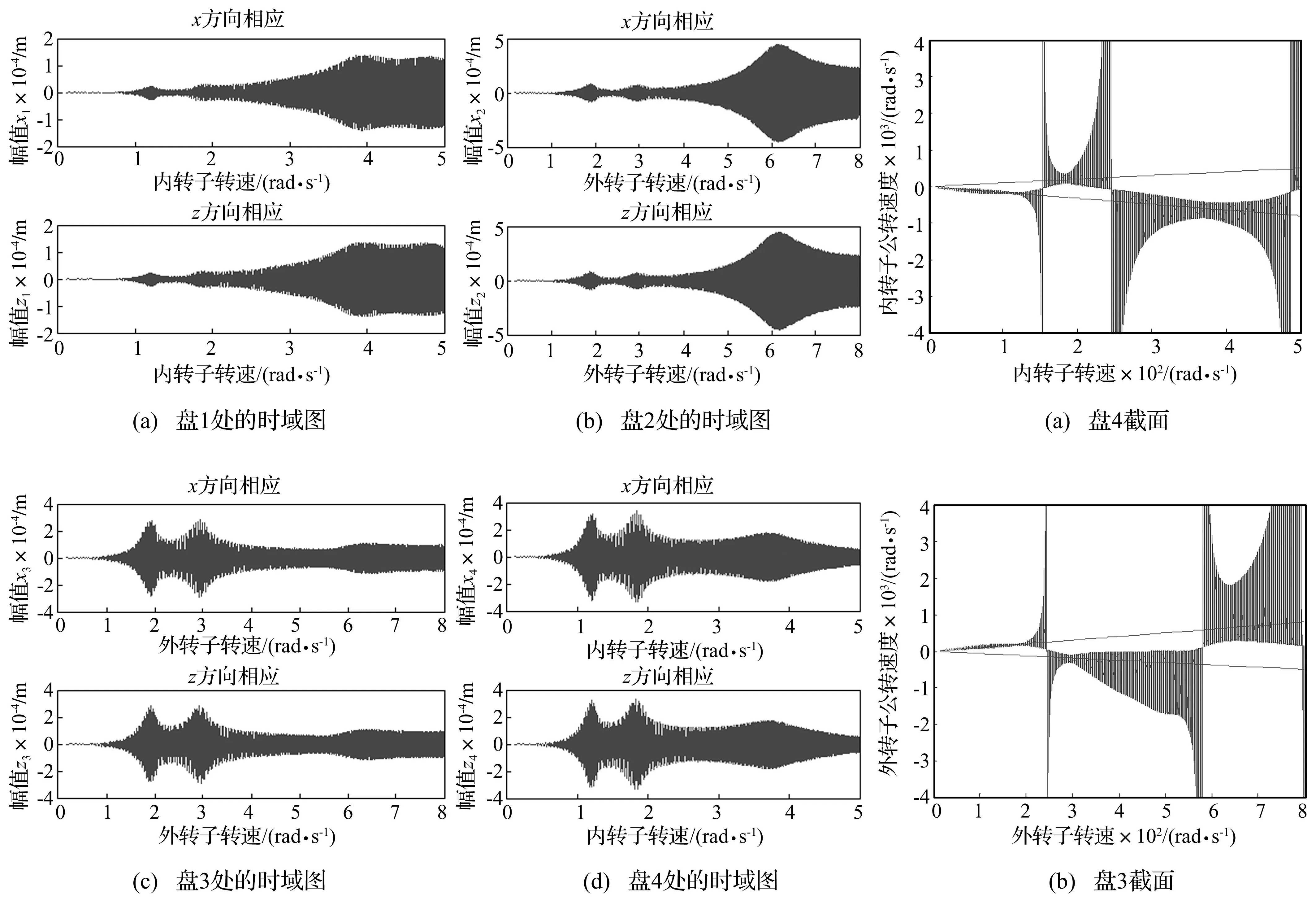
图7 双转子系统各截面处时域响应

2.3 试验验证

用4个电涡流位移传感器分别测量内外转子互相垂直的两方向振动响应(图2)。在盘3、盘4外环处粘贴窄铜片记录相位，用传感器Op，Ip记录转子相位信息，转子运行时内外转子反向旋转。限于试验条件，该试验器加速过程中仅能通过转子一阶临界转速。传感器Ix的三维频谱见图11，该图反应出试验器的加速过程及跨越临界转速时转子响应状态，存在内外转子两个不平衡激励频率。

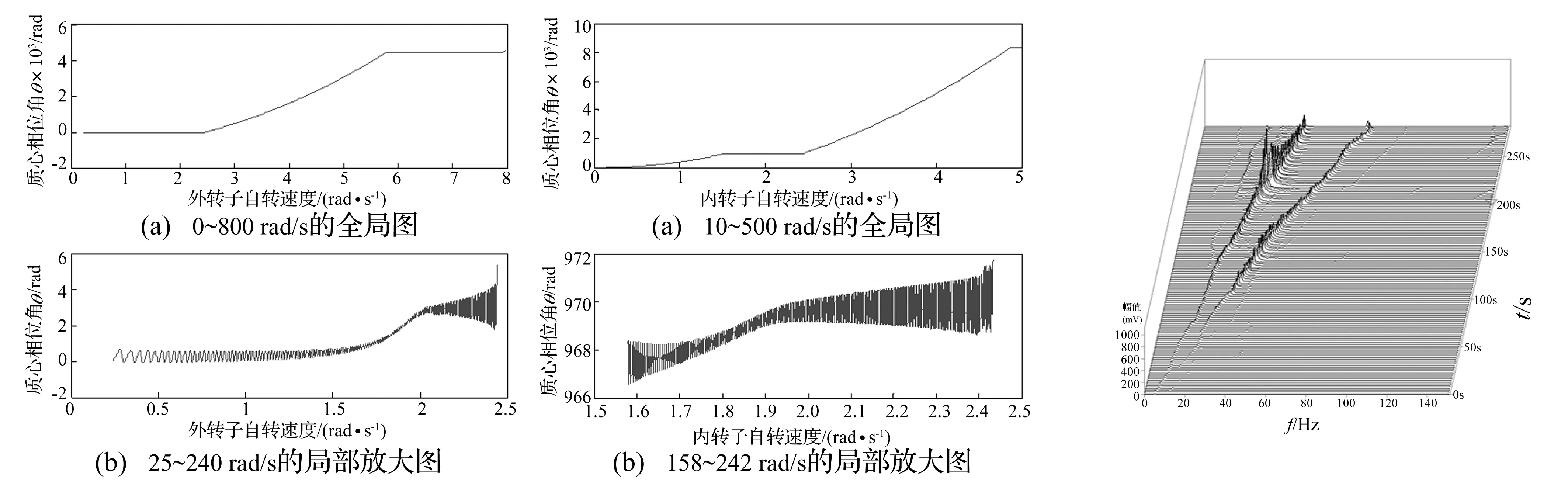
图9 外转子质心随时间变化规律(盘3)

图12 内转子加速响应时域图(传感器为Ix,Iz)

内外转子加速瞬态时域响应见图12、图13。由二图看出，内外转子分别出现以外转子为主激励及内转子为主激励的一阶临界转速引起的峰值，且响应峰值均较明显，与2.2.1节计算结果吻合。

试验中内外转子在外转子为主激励的一阶临界转速与内转子为主激励的一阶临界转速之间进动转速变化见图14。对比图14、图8知，试验结果与计算结果较吻合。

用传感器Op信号与传感器Oz信号及传感器Ip信号与传感器Iz信号做李莎如图，该图中脉冲位置的变化可用于分析转子盘质心相位角变化。由图15可知，在外转子为主激励的一阶临界转速前后，外转子相位角的相位变化约为π，在临界转速时变化约为π/2，相位角围绕一定角度上下波动。在以内转子为主激励的一阶临界转速前后变化趋势与外转子趋势相同，不再赘述。与2.2.3节理论分析相符。

3 结 论

本文据固定界面模态综合法思想建立反向旋转双转子试验器的瞬态动力学模型，用有限元软件获取各子结构模态特性；用Newmark法对系统模态空间中瞬态动力学模型进行求解；分析反向旋转双转子系统加速过程中瞬态时域特性、进动转速变化特性及内外转子盘质心变化规律，结论如下：

(1) 所用固定界面模态综合法对转子瞬态特性研究具有较高效率与精度。

(2) 反向旋转双转子系统瞬态响应特性与各界临界转速及振型联系密切，且转子不同截面处瞬态响应特性有一定差异。

(3) 反向旋转双转子系统从某阶临界转速向下一阶临界转速变化中，转子进动转速存在剧烈变化过程，转子处于较强烈的非协调进动状态。

(4) 内外转子质心换向过程分别出现在以各自为主激励的临界转速附近，且质心相位角围绕某一定值上下波动。

本文结论可为更全面分析、理解反向旋转双转子系统动力特性提供分析方法及理论支持，也可为反向旋转双转子系统试验测试、分析提供指导。为进一步分析、预测该系统非线性动力特性奠定基础。

参 考 文 献

[1]Childs D W. A modal transient rotordynamic model for dual-rotor jet engine systems[J]. Journal of Engineering for Industry, 1976, 98 (3): 876-882.

[2]Stallone M J,Gallardo V,Storace A F,et al.Blade loss transient dynamic analysis of turbomachinery[J]. Source:AIAA Journal, 1983, 21(8): 1134-1138.

[3]Alam M. Nelson H D.Blade loss response spectrum for flexible rotor systems[J]. Source: Journal of Engineering for Gas Turbines and Power, 1985, 107(1): 197-204.

[4]Sun G Y, Palazzolo A B, Carney K, et al. An efficient algorithm for blade loss simulations using a high fidelity ball bearing and damper model[J]. Source: Proceedings of the ASME Design Engineering Technical Conference, 2003, 5(B): 1011-1020.

[5]Sun G Y, Palazzolo A B, Provenza A,et al. Long duration blade loss simulations including thermal growths for dual-rotor gas turbine engine[J]. Source: Journal of Sound and Vibration, 2008, 316(1-5): 147-163.

[6]晏砺堂,王德友．航空双转子发动机动静件碰摩振动特征研究[J]. 航空动力学报, 1998,13(2): 173-176.

YAN Li-tang,WANG De-you. Vibration features from rubbing between rotor and casing for a dual-shaft aeroengine[J]. Journal of Aerospace Power, 1998,13(2):173-176.

[7]周海仑,陈 果. 航空发动机双转子-滚动轴承-机匣耦合系统动力学分析[J]. 航空动力学报,2009,24(6):1284-1291.

ZHOU Hai-lun, CHEN Guo. Dynamic response analysis of coupling system dual rotor-ball bearing-stator for aero-engine[J]. Journal of Aerospace Power, 2009, 24(6): 1284-1291.

[8]Han Q K,Luo H T, Wen B C. Simulations of a dual-rotor system with local rub-impacts based on rigid-flexible multi-body model[J]. Source: Key Engineering Materials, 2009, 413-414: 677-682.

[9]Lalanne M, Ferraris G. Rotordynamics prediction in engineering[M]. England: Wiley, 1989.

[10]Gupta K, Gupta K D, Athre K. Unbalance response of a dual rotor system: theory and experiment[J]. Journal of Vibration and Acoustics, 1993, 115(4):427-435.

[11]Ferraris G. Prediction of the dynamic behavior of non-symmetric coaxial co-or counter rotating rotors[J]. Journal of Sound and Vibration,1996,195(4): 649-666.

[12]冯国权, 岳承熙,张连祥. 对转式双转子发动机机动特性分析[J]. 航空发动机, 1993(5):43-48.

FENG Guo-quan, YUE Cheng-xi, ZHANG Lian-xiang. Dynamic analysis of a two-spool engine with counter rotating rotors[J]. Aeroengine, 1993(5): 43-48.

[13]冯国权,张连祥,伊 峰.反向旋转的双转子发动机稳态不平衡响应分析[J]. 哈尔滨工业大学学报,1998,30:249-252.

FENG Guo-quan, ZHANG Lian-xiang, YI Feng. Stationary unbalance response analysis of a two-spool engine with counter rotating rotors[J]. Journal of Harbin Institute of Technology, 1998, 30: 249-252.

[14]胡 绚，罗贵火，高德平. 反向旋转双转子稳态响应计算分析与试验[J]. 航空动力学报，2007,22(7):1045-1049.

HU Xuan, LUO Gui-huo, GAO De-ping. Numerical analysis and experiment of counter-rotating dual-rotor’s steady-state response[J]. Journal of Aerospace Power, 2007,22(7): 1045-1049.