基于微分求积法分析旋转圆板的横向振动

王忠民， 王 昭， 张 荣， 李会侠

(西安理工大学 土木建筑工程学院，西安 710048)

旋转圆板在航空、航天、机械工程等高科技领域有着广泛的应用，如涡轮发动机、计算机硬盘和光驱等。在运行过程中，其弯曲振动会导致失稳和断裂，从而使得旋转机械系统发生破坏，因此，旋转圆形薄板振动和稳定性的研究具有重要的实际意义。由于旋转圆板受径向离心惯性力的作用，使得运动微分方程的系数为变系数，从而求解和分析难度增大。几十年来，一些学者对于旋转圆板的横向振动问题进行了系统的研究。关于2006年以前研究成果可参看文献[1]。Bauer等[1]对等厚度旋转圆板的横向振动和稳定性问题，采用Ritz-Galerkin法求解变系数运动微分方程，得到了不同边界条件下旋转圆板的固有频率随角速度的变化规律。Baddour等[2]考虑了旋转圆盘的面内惯性效应的影响，建立了旋转圆盘面内和横向振动的非线性耦合模型，采用Galerkin和正则摄动法，得到了圆盘的内共振及不稳定的可能性。Ranjan等[3]用有限单元法分析了在圆心处带有刚性核的旋转圆盘自由和强迫振动，并研究了压电片对旋转圆盘的振动控制问题。Hasheml等[4]对转动厚板，基于Mindlin板理论和二阶应变—位移关系，应用Kane动力学方法导出了非线性运动微分方程，采用有限元法，分析了边长比、厚度比、轮毂半径比和圆盘转速对固有频率的影响。Khorassny等[5]采用模态展开法，研究内边界沿轴向可自由移动、外边界由线弹簧约束的环形旋转圆盘的线性振动行为，以及刚性平移、向前或向后行波对系统稳定性的影响等。Genta等[6]发展了环形有限元法，研究了旋转叶盘的二阶和高阶谐波振型，拓展了以往研究局限于零解和一阶谐波振型的研究。Li等[7]采用Galerkin法，分析了转动层合板向前和向后行波的动力特性。在上述求解方法中，Galerkin法或模态展开法求解的精度在很大程度上受到了模态函数的选取以及项数的制约。

本文对旋转实心圆板，针对在沿径向线性分布离心惯性力作用下的旋转圆板的变系数运动微分方程，采用微分求积法离散方程和边界条件，得到了周边固支、简支(且沿径向不可移)和周边完全自由三种边界条件下旋转圆板的前两阶复频率的实部和虚部随旋转角速度的变化情况，有效地分析了旋转圆板的横向振动特性和稳定性。

1 旋转圆板的横向振动微分方程

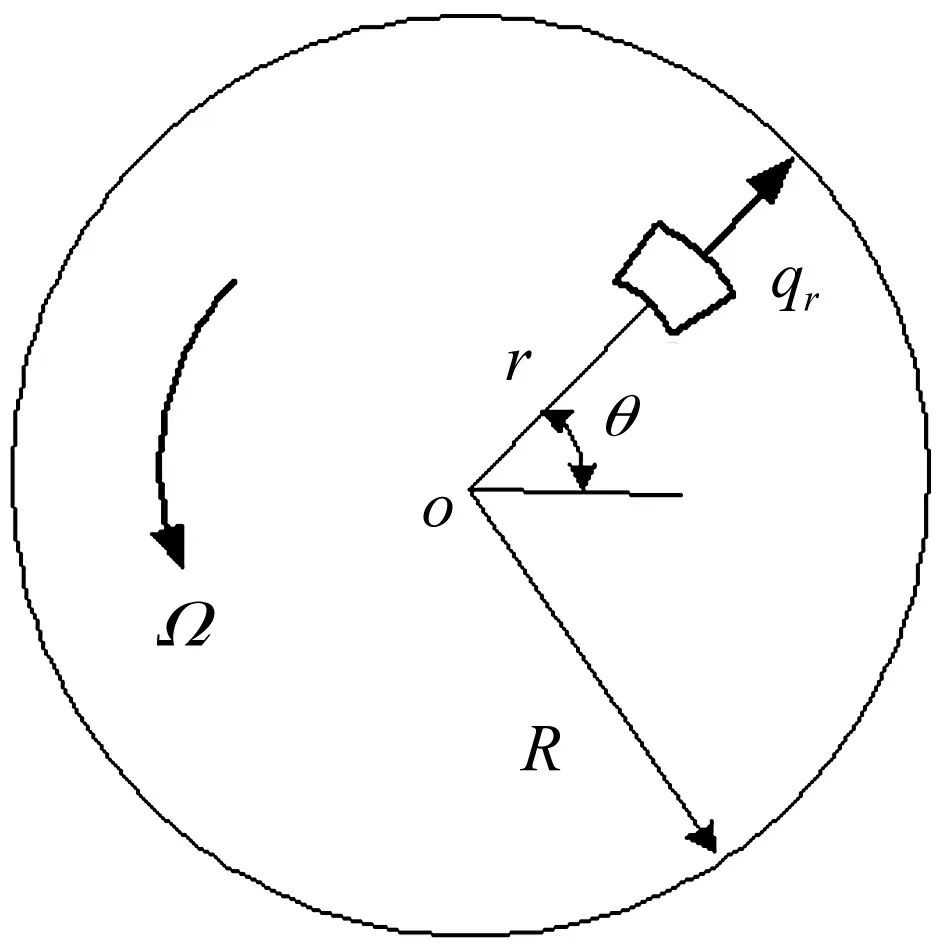
图1 旋转圆板示意图

板厚为h、半径为R的等厚度圆板绕其中心轴O以常角速度Ω旋转如图1所示。设材料密度为ρ，弹性模量为E，泊松比为ν，板的抗弯刚度为D。选取极坐标，径向坐标为r，环向坐标为θ，单位面积的径向惯性力可表示为qr=ρhΩ2r，即是在板中面内的沿径向的线性分布力。基于Kirchhoff薄板理论[8]，旋转圆板以横向挠度w(r,t)表示的运动微分方程为:

(1)

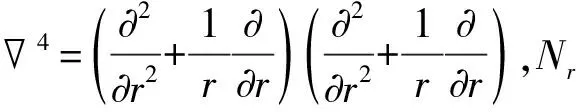
1.1 基于弹性力学的平面应力问题求解Nr和Nθ

匀速旋转圆形薄板在离心惯性力作用下，其几何、载荷和约束情况均为轴对称，应力分量与环向坐标θ无关，且τrθ为零。设ur为圆板中面内的径向位移(环向位移vθ=0)，由径向的平衡微分方程、物理方程、平面轴对称问题的几何方程和引入的应力函数φ(r)[9]得:

(2)

(3)

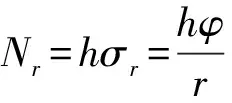
1.1.1 周边固支和周边简支板

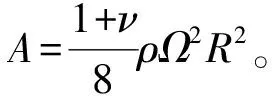
(4)

(5a)

(5b)

1.1.2 周边自由板

对周边自由板，边界条件为σrr=R=0，得[9]

(6)

(7a)

(7b)

1.2 运动微分方程及边界条件

引入下列无量纲量:

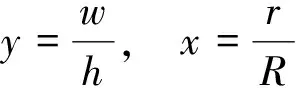
(8)

则方程(1)以无量纲量可表示为:

(9)

对周边固支和周边简支板，有:

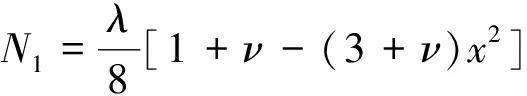
对周边自由板，有:

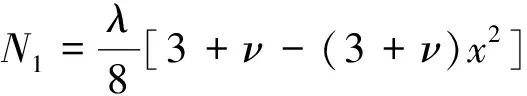
式中,λ称为无量纲角速度。

(10)

式中ω为系统的无量纲振动频率。

在圆心x=0处，以无量纲量表示的边界条件为:

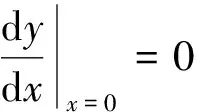
(11)

在外周边(x=1)处，三种边界条件分别为:

固支：

(12)

简支：

(13)

自由：

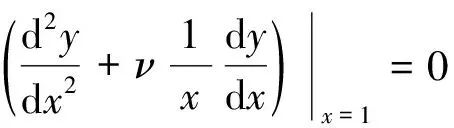
(14)

2 DQ法求解

微分求积法[10-11](简称DQ)的实质是用全域上全部节点的函数值进行加权求和来表示函数及其导数在给定节点处的值，因而可以将微分方程离散成以节点处的函数值为未知数的一组代数方程组。以一元函数y(x)为例，设在区间[0,1]上连续可微，其一阶导数可写为

(15)

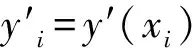
(16)

类似的，在第i个节点处函数的二阶、三阶、四阶导数值可表示为

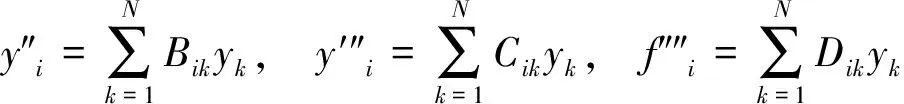
(17)

式中:Bik、Cik、Dik分别称为二阶导数、三阶导数、四阶导数的加权系数。各阶导数加权系数之间的关系为

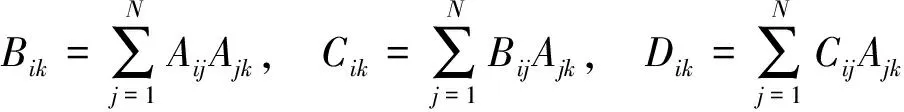
(18)

DQ法中的两个关键因素：一是如何确定权系数;二是如何布置节点。本文中，插值基函数采用Lagrange多项式，节点的选取形式为

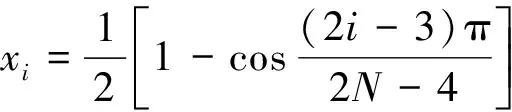
(19)

对含变系数的四阶常微分方程(10)，其微分求积形式为

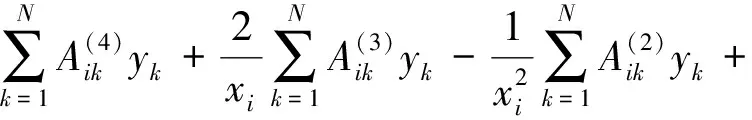
(20)

在式(20)中，若外边界为简支和固支，有

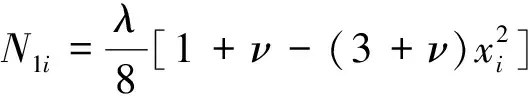
若为自由边

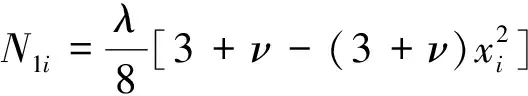
在圆心x=0处，边界条件的微分求积形式为

(21a)

(21b)

在外周边x=1处，边界条件(12)、(13)、(14)的微分求积形式分别为:

固支：

(22)

简支：

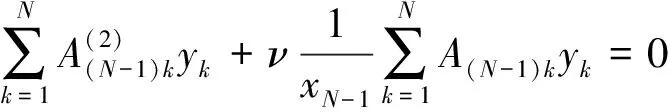
(23)

自由：

(24a)

将式(20)和边界条件的微分求积形式联立，写成矩阵形式

(ω2[Q]+[K]){y}=0

(25)

其中[Q]、 [K]为方阵；{y}为由振型函数在各节点处函数值组成的向量。根据线性代数理论，方程组(25)存在非零解的充分和必要条件是系数行列式等于零，即得特征方程

|ω2[Q]+[K]|=0

(26)

3 数值计算与分析

为了说明上述方法的有效性，首先计算无旋转实心圆板的横向轴对称自由振动问题，这只要在振型微分方程(10)中令λ=0即可。在三种边界条件下圆板的横向轴对称自由振动问题的前四阶固有频率与已有解的比较如表1所示，其中对周边自由的圆板存在与刚体振型相应的零固有频率。计算中节点数N=13。

对旋转圆板，角速度对圆板的横向轴对称振动特性及稳定性有很大的影响。下面计算三种周界约束下旋转圆板的无量纲固有频率与无量纲角速度的变化关系，分析其横向振动特性及稳定性。

3.1 周边简支的旋转圆板

在周边为简支且沿圆板径向不可移的约束条件下，旋转圆板前两阶无量纲固有频率与无量纲角速度的变化曲线如图2所示。从图2可知，当无量纲角速度λ=0时，ω为实数，即为圆板自由振动的无量纲固有频率。随着无量纲角速度的增加，无量纲固有频率实部Re(ω)减小，虚部lm(ω)保持为零。当无量纲角速度增加到λ1=3.96时，第一阶模态频率的实部Re(ω)变为零，此后Re(ω)一直为零，而虚部lm(ω)为正负两个分支， 这说明旋转圆板呈现了发散失稳。因而无量纲临界角速度λ1=3.96又称为第一阶临界发散角速度。同样对二阶无量纲固有频率与无量纲角速度的变化曲线也有类似的特性，λ2=100.9称为第二阶临界发散角速度。

3.2 周边固支的旋转圆板

在周边为固支且沿圆板径向不可移的约束条件下，旋转圆板前两阶无量纲固有频率与无量纲角速度的变化曲线如图3所示。与周边简支的旋转圆板不同的是，其一、二阶无量纲固有频率随着无量纲角速度从零的增加，无量纲固有频率实部Re(ω)非单调减小，而是先增大再减小。其失稳特性和周边简支的旋转圆板相同，即均为一阶、二阶模态上发散失稳，一、二阶无量纲临界发散角速度分别为λ1=39，λ2=205.9。

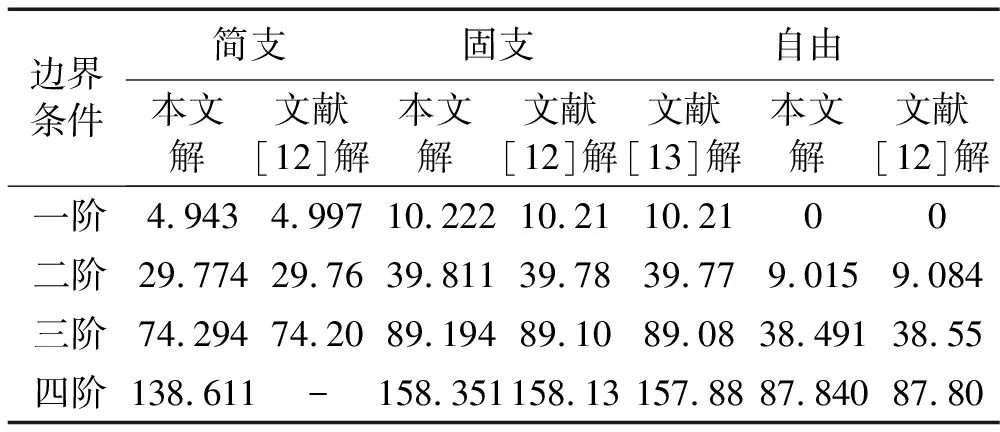
表1 三种边界条件下实心圆板的前四阶轴对称固有频率与已有解的比较

图2 周边简支旋转圆板的ω随λ的变化情况

3.3 周边自由的旋转圆板

在周边完全自由的情况下，由无旋转圆板(或静止圆板，见表1)和旋转圆板的计算结果知，出现了零固有频率，其振型相应于圆板的刚体平移运动。从周边自由的旋转圆板前两阶无量纲固有频率与无量纲角速度的变化曲线(图4)可知，随着无量纲角速度的增加，旋转圆板前两阶无量纲固有频率(即复频率的实部)也在增大，且复频率的虚部为零，不存在无量纲临界角速度和失稳。出现这一现象的原因是，对周边完全自由圆板，在沿圆板径向线性分布的离心惯性力作用下，从式(7a)和式(7b)知，圆板面内板单位宽度的径向拉压力Nr和环向拉压力Nθ均为拉力。随着无量纲角速度的增大，Nr和Nθ线性增大，使得圆板的挠度减小，因相当于增加了旋转圆板的弯曲刚度，从而使无量纲角速度增大。

与完全自由旋转圆板不同，对周边为固支、简支且沿圆板径向不可移的旋转圆板，在沿圆板径向线性分布的离心惯性力作用下，由于沿圆板径向不可移约束的作用，从式(5a)和式(5b)知，圆板面内板单位宽度的径向拉压力Nr和环向拉压力Nθ为负值，即为压力。因此对周边为固支和简支旋转圆板，呈现了无量纲角速度减小且趋于零的现象，使圆板发生了静力失稳。

图3 周边固支旋转圆板的ω随λ的变化情况

图4 周边自由旋转圆板的ω随λ的变化情况

4 结 论

基于薄板的小变形理论，采用微分求积法，研究了均质等厚度匀速旋转圆板的横向振动和稳定性问题，得到了周边固支、简支(沿径向不可移)和周边完全自由三种边界条件下旋转圆板的前两阶复频率的实部和虚部随旋转角速度的变化情况。对周边固支、简支旋转圆板，一般来说，复频率的实部随角速度的增大而减小且趋于零，得到了一、二阶临界发散角速度；对周边完全自由旋转圆板，复频率的实部随角速度的增大而增大，不发生失稳现象。上述结论对旋转圆盘系统的设计与运行提供了一定的参考依据。

参 考 文 献

[1]Bauer H F, Eidel W. Transverse vibration and stability of spinning circular plates of constant thickness and different boundary conditions [J]. Journal of Sound and Vibration, 2007, 300(3-5)：877-895.

[2]Baddour N, Zu J W. Nonlinearly coupled in-plane and transverse vibrations of a spinning disk[J]. Applied Mathematical Modelling, 2007,31(1)：54-77.

[3]Ranjan V, Ghosh M K. Transverse vibration of spinning disk with attached distributed patch and discrete point masses using finite element analysis [J]. International Journal of Engineering, Science and Technology, 2009,1(1)：74-89.

[4]Hashemi S H, Farhadi S, Carra S. Free vibration analysis of rotating thick plates [J]. Journal of Sound and Vibration, 2009,323(1-2)：366-384.

[5]Khorasany R M H, Hutton S G. An analytical study on the effect of rigid body translational degree of freedom on the vibration characteristics of elastically constrained rotating disks [J]. International Journal of Mechanical Sciences, 2010,52(9)：1186-1192.

[6]Genta G, Feng C, Tonoli A. Dynamics behavior of rotating bladed discs：A finite element formulation for the study of second and higher order harmonics[J]. Journal of Sound and Vibration, 2010,329(25)：5289-5306.

[7]Li L F, Wang X Z, Zhou Y H. Dynamic characteristics of traveling waves for a rotating laminated circular plate with viscoelastic core layer [J]. Journal of Sound and Vibration, 2011, 330(12)：2836-2847.

[8]Timoshenko S， Woinowsky-Krieger S. Theory of Plates and Shells [M]. Second edition, McGraw-Hill, New York, 1959.

[9]徐芝纶. 弹性力学(第四版，上册).[M]. 北京：高等教育出版社出版，2006.

[10]Bert C W, Malik M. Differential quadrature method in computational mechanics：a review [J]. Applied Mechanics Review,1996, 49(1)：1-28.

[11]程昌钧，朱正佑. 微分求积方法及其在力学应用中的若干新进展[J]. 上海大学学报(自然科学版), 2009,15(6)：551-559.

CHENG Chang-jun,ZHU Zheng-you. Recent Advances in Differential Quadrature Method with Applications to Mechanics [J]. Journal of Shanghai University, (Natural Science Edition)2009,15(6)：551-559.

[12]倪振华. 振动力学 [M]. 西安:西安交通大学出版社, 1990.

[13]王忠民, 高敬伯, 李会侠. 非保守圆薄板的轴对称振动和稳定性[J]. 固体力学学报, 2003, 24(2)：155-162.

WANG Zhong-min, GAO Jing-bo, LI Hui-xia. Axially symmetric vibration and stability of circular thin plate subjected to non-conservative forces [J]. ACTA Mechanical Solida Sinica, 2003, 24(2)：155-162.