粗糙界面法向接触振动响应与能量耗散特性研究
2014-09-05肖会芳邵毅敏徐金梧
肖会芳, 邵毅敏, 徐金梧
(1.北京科技大学 国家板带生产先进装备工程技术研究中心,北京 100083;2.重庆大学 机械传动国家重点实验室,重庆 400044)
动力系统中,结构之间通过接触界面进行动力传递。界面不仅极大地影响机械装备振动测量信号的特征[1],而且是影响机械零件性能,诸如动态性能、接触疲劳强度、摩擦功耗和磨损寿命等至关重要的因素[2]。
目前,关于接触界面振动响应与能量耗散的研究几乎都集中在沿接触界面切向的滑动摩擦耗散[3-5]。尽管关于无润滑法向接触振动能量耗散的实验研究表明,并未观察到明显的法向微动能量耗散,但却尚未从理论上予以解释[6]。经典的Hertz球体接触理论被广泛地用于描述接触界面法向的力-变形关系、接触面积以及压力分布特征[7]。实际中,通过机械加工处理的工程结构表面,并非绝对平滑,而是具有不同程度的粗糙度[8-9]。对粗糙接触界面而言,其法向接触具有怎样的力-变形关系,接触振动具有怎样的动力学响应特性,能量耗散具有怎样的特征与机理,与Hertz接触模型相比有何异同,对描述界面动力学机理具有重要的理论和实际意义。
本文建立粗糙界面法向接触振动的动力学模型,提出了不同形貌粗糙界面法向接触振动的动力学响应特征量和振动能量耗散量的计算方法,并构造了粗糙接触界面的接触力-变形关系;建立了接触振动系统的动力学方程,计算了不同形貌粗糙界面法向接触振动每周期的振动能量耗散率和累积振动能量耗散率;分析了粗糙界面法向接触振动的响应特征与能量耗散特性;从理论上解释了文献[6]的实验结果。
1 粗糙界面法向接触振动模型
1.1 动力学模型描述
研究粗糙界面法向接触振动与能量耗散特性的模型示意图,如图1所示。金属板与刚性平面的接触面为具有一定表面形貌的三维粗糙表面。在法向载荷作用下,金属板在固定的刚性平面上进行接触振动。由于存在界面阻尼,其振动过程伴随着能量耗散。

图1 粗糙界面法向接触振动模型示意图
图1所示模型的动力学特性可以采用单自由度模型进行描述,如图2所示。该单自由度模型被广泛地用于描述Hertz“球-刚性平面”接触振动[10-12]。其假设条件是小球质量中心的位移量与局部接触区域的位移量相同,即小球的变形仅发生在局部接触区域[7]。其中,弹簧的回复力为Hertz弹性接触公式的力-变形关系式,阻尼模型为线性粘弹性阻尼。
对图1所示的粗糙界面接触模型,其接触变形几乎完全发生在接触区的粗糙体,质量中心的位移量与局部接触区域的位移量一致[13]。基于该特征,其接触振动模型也可采用图2所示的单自由度模型进行描述。其中,弹簧的回复力为粗糙表面与刚性平面之间的弹性接触力-变形关系式。对无润滑界面,阻尼特性采用线性粘性阻尼模型表征[10]。
尽管对粗糙界面,由于实际接触面仅为一些点和很小的面,因而容易在接触点发生应力集中,使应力值高于屈服应力而产生塑性变形[13],纯弹性接触几乎不存在。但对界面的法向接触振动而言,通常的情况是接触体在静平衡位置附近振动。此时,塑性变形产生于接触体达到静平衡位置的过程中,而其微振动则仍属于弹性接触范围[14]。

图2 接触振动的单自由度模型
1.2 动力学方程
图2所示的单自由度模型在静平衡位置附近的自由振动方程可以表示为:
(1)
其中:m为金属板质量,c为阻尼系数,fk(z,zs)为弹性回复力,即为粗糙界面的弹性接触力-变形关系式,zs为金属板在重力作用下的静变形量。对于式(1),为了保持金属板与刚性平面接触,必须符合z≥-zs。
采用如下的无量纲位移u,无量纲时间τ,无量纲阻尼比ζ和线性接触频率参数ωs,对式(1)进行无量纲化
其中,k(zs)为静平衡位置处的接触刚度。则式(1)对应的无量纲表达式为:
(2)

(3)
其中,无量纲的激励幅值和激励频率分别为:
系统的无量纲初始条件为u(τ0)=u0,u′(τ0)=v0。对式(2),金属板与刚性平面接触的条件变为u≥-1。
2 接触振动响应特征量与能量耗散量计算方法
为了获得图1所示接触振动模型的动力学响应特征量与能量耗散量,首先需要确定式(1)的弹性力-变形关系表达式fk(z,zs)。
2.1 粗糙界面接触力-变形关系式计算方法
基于粗糙表面的三维分形模型描述[13,15],通过建立三维粗糙表面模型,采用有限元方法,对图1所示粗糙界面模型进行弹性接触计算分析,获得不同表面形貌接触界面的接触力-变形关系式[13,16]。
三维分形表面采用修正的两参数Weierstrass-Mandelbrot函数描述,其表达式为[15]

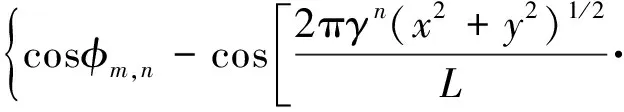
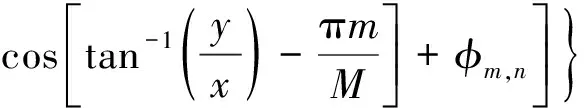
(4)
其中,L为样本长度,Ls为截断长度,γ(γ>1)为缩放参数,M为生成分形表面的脊线数,n是频率因子,nmax=int[log(L/Ls)/logγ],Φm,n是[0,2π]内的随机相位。表面粗糙程度由尺度独立的分形参数D和G控制。表面分形维数D,其物理意义是粗糙表面所占据的空间程度大小,D值越大对应于越密集的表面形态(更光滑的表面形貌)。表面分形粗糙度G是高度尺度参数,G值越大对应越粗糙的表面形貌。参数D和G一般通过实验测试确定。根据实验结果,D的范围为[2.3,2.7],G的范围为[1.36E-13,1.36E-10]m[15]。
采用式(4)生成的具有不同表面形貌的0.9 μm×0.9 μm三维分形表面,如图3所示。其中,Ls=1.5E-7m,M=10,γ=1.5[15],D=2.4。图3显示,对相同的分形维数D,增大表面分形粗糙度G的表面形貌更粗糙。
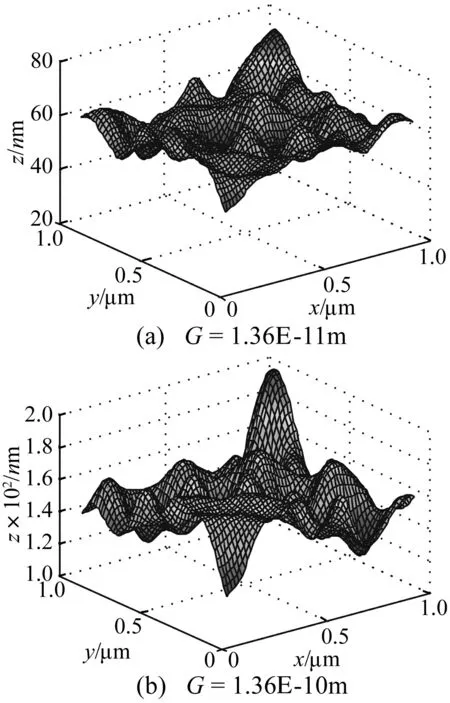
图3 不同表面形貌的三维分形粗糙表面
2.1.1 有限元计算模型
有限元计算模型示例,如图4所示。三维金属板用SOLID185单元离散,SOLID185单元的每个节点具有3个方向的平动自由度。金属板与刚性平面之间建立接触对,接触对通过点-面接触单元对TARGE170 和CONTA175识别。接触单元CONTA175覆盖在金属板的接触表面,用来描述变形体的边界条件,并与目标单元TARGE170进行接触。刚性平面全约束,金属板的上表面节点仅具有Z方向的自由度。在金属板的上表面节点施加均布的位移载荷,求取刚性平面的反力,获得金属板与刚性平面之间的接触力。计算过程中,位移载荷通过多个载荷子步逐渐施加,最大载荷步和最小载荷步分别设置为400和50。接触算法采用Augmented Lagrangian算法。力的收敛准则设为0.001。

图4 有限元计算模型(D=2.3,G=1.36E-11m)
2.1.2 有限元计算方法有效性的验证
采用限元方法模拟Hertz接触与Hertz理论计算结果对比的方法,检验本文所采用的有限元计算方法处理接触问题的有效性。计算模型为半径为R=8 mm的球在法向力F=5 kN的作用下与刚性平面进行无摩擦接触。材料的属性参数为弹性模量E=30 GPa,泊松比ν=0.25。建立Hertz接触的有限元模型的方法、离散球体的单元类型、识别界面接触的接触单元类型以及接触算法与建立粗糙界面接触的有限元模型保持一致。通过有限元计算求解接触半宽b和接触变形量d,并与Hertz接触理论计算结果对比[7],如表1所示。从表中可以看出,有限元计算结果与Hertz理论计算结果的误差小于3%,表明本文所采用的有限元计算方法是准确、可靠的。

表1 有限元和Hertz理论计算结果对比
2.2 振动响应特征量与能量耗散量计算方法
通过计算获得的接触力-变形关系,求解动力学方程式(1),可以获得其振动响应特征量和能量耗散量。粗糙界面法向接触自由振动的振动响应特征通过瞬时频率和等效阻尼比描述。能量耗散特性则通过每周期的能量耗散率和一段时间内的累积能量耗散率描述。
2.2.1 瞬时频率
由于接触振动系统的非线性特性,系统自由振动每周期内的频率并不相同,而随幅值变化。假设每个振动周期内的响应可以表示为:
u=Ucos(Ωτ+φ)
(5)
其中,U,Ω和φ分别为瞬时幅值、瞬时频率和瞬时相位,在单个周期内保持恒定,且:
(6)
瞬时频率可以表示为
(7)
其中,Δτ为相邻峰之间的时间间隔。
2.2.2 等效阻尼比
对自由振动系统,描述其响应特征的等效阻尼比可以采用对数衰减率进行估算,其表达式为:
(8)
其中,δ为对数衰减率,Ui为第i个振动周期的幅值(i=1,2,3,…)。
2.2.3 能量耗散率
自由振动每周期的能量耗散量可表示为

(9)
式中:τ1和τ2为相邻峰值对应的时间,fd为阻尼力,其表达式为:
fd(u′)=2ζu′
(10)
将式(5),式(10)代入式(9),并定义φ=Ωτ+φ,每周期的能量耗散量可以表示为:
(11)
式(11)显示,系统每周期的能量耗散量由瞬时频率、瞬时振幅、瞬时相位和阻尼比决定。
进一步定义系统每周期的能量耗散率为每周期的能量耗散量与输入能量的比值
(12)
其中,Ein为系统的输入能量,在初始条件为u(τ0)=u0,u′(τ0)=v0时,其表达式为:

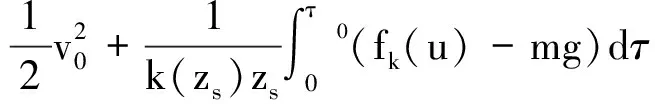
(13)
系统在从自由振动开始时刻τ0到任意时刻τ内的累积能量耗散率为:
(14)
3 数值计算结果分析
3.1 粗糙界面弹性接触力-变形关系表达式
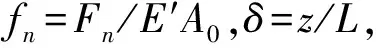
界面无摩擦,表面形貌参数不同,最大法向位移δ=0.1时的力-变形曲线,如图5所示。其中,图5(a)为粗糙表面的表面分形粗糙度G=1.36E-11m,而表面分形尺度参数D不同,分别为D=2.3,2.4,2.5,2.6;图5(b)为表面分形尺度参数D=2.4,而表面分形粗糙度G不同,分别为G=1.36E-10m,1.36E-11m,1.36E-12m,1.36E-13m。
图5显示,界面的接触力随变形非线性递增,接触刚度呈非线性递增(曲线的斜率逐渐增大);不同表面粗糙度界面的非线性有所差异:粗糙度较大的界面(较小的D值或较大的G值)具有更强的非线性(曲线斜率的变化更剧烈)。相同位移载荷下,粗糙度较大界面的接触力小于粗糙度较小的界面;随着接触表面的粗糙度逐渐变小,界面的接触力-变形关系逐渐接近于绝对平滑界面。
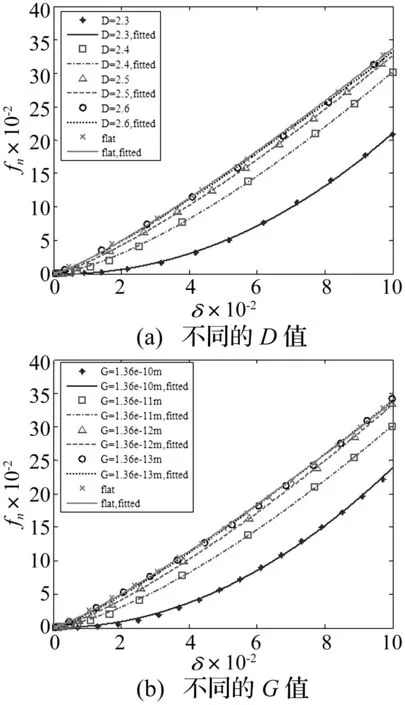
图5 界面无摩擦,不同形貌界面的接触力-变形曲线
进一步考虑界面摩擦对接触力-变形关系的影响。界面存在摩擦的计算方法与前文相同,不同的是界面处增加了摩擦因子μ=0.2。此时,不同表面形貌粗糙界面的接触力-变形曲线,如图6所示。与界面无摩擦曲线相比,界面存在摩擦时:力-位移曲线形状一致,即界面的接触刚度变化趋势一致;在相同位移下,接触力数值增大。
不同表面形貌界面的接触力与变形关系可用指数函数式(15)表示:
fn(δ)=kδα
(15)

图5和图6的拟合结果表明:式(15)能很好地描述粗糙界面的接触力-变形关系,表达式中的各系数数值,如表2所示。为验证力-变形关系式(15)的有效性,对比了不同表面粗糙度值G的摩擦界面(图6(b))力-变形关系式与数值计算结果间的相对误差,如图7所示。最大相对误差为3.4%,最小相对误差为0.05%,图7所示结果表明式(15)可准确地表征实际计算结果。
上述计算结果基于尺寸为0.9 μm×0.9 μm的分形表面模型。由于分形表面的自相似特性,表面形貌模型与尺度无关[15]。因而,式(15)同样适用于其他尺寸。

图6 界面存在摩擦,不同形貌界面的力-变形曲线
3.2 粗糙界面接触与Hertz接触力-变形关系式对比分析
表2显示:受表面粗糙度和界面摩擦的影响,式(15)所示非线性力-变形关系指数α的范围为α=[1.168,2.195];且随着表面粗糙度减小(D值较大或G值较小,接触界面更光滑),系数k和指数α逐渐减小。
表2所示的最大和最小α值对应的力-变形曲线,以及Hertz接触理论的力-变形关系曲线,如图8所示。图8显示,对不同的α值,曲线所示的非线性度以及回复力的大小存在较大的差异。因而,与Hertz接触理论相比,对粗糙接触界面,其力-变形关系仍然具有指数函数关系式;不同的是,受表面粗糙度的影响,指数函数的指数范围为α>1,而非α=3/2。
3.3 接触振动响应与能量耗散特性
基于获得的粗糙界面接触力-变形关系式(15),式(1)所示的自由振动方程可以表示为:
(16)
式(2)所示的无量纲表达式为
(17)

3.3.1 瞬时频率
求解式(17)所示的非线性振动方程。其中,不同表面粗糙度对应的接触刚度模型以α=1,3/2,2和5/2为例进行描述;冲击载荷的幅值为σ=0.6,频率为Ω0=1;计算采用的阻尼系数为ζ=0.005[10-11]。
采用式(7)计算不同接触刚度模型自由振动响应对应的瞬时频率,如图9所示。图9显示,对不同的刚度模型(表面粗糙度),其振动瞬时频率存在较大差异:对刚度指数为α=1的线性系统,瞬时频率保持Ω=1不变;对刚度指数为α=3/2,α=2和α=5/2的非线性系统,瞬时频率随着幅值的增大而减小,其最大值为Ω=1,对应于静平衡位置U=0;随着非线性刚度指数α增大,瞬时频率随幅值的变化更剧烈,系统具有更强的非线性。同时,图9显示,相对于线性系统,不同刚度指数对应的非线性系统的瞬时频率随幅值的减小量很小,表明该激励载荷下的系统仅表现出较弱的非线性;随着激励载荷增大,其非线性会增强。

图8 具有不同指数大小的非线性指数函数力-变形关系曲线fn(δ)= δα
系统振动的瞬时频率随着振幅的增大而增大,表明系统具有硬弹簧特征;反之,系统则具有软弹簧特征[17]。因此,刚度指数为α>1的系统均对应于软弹簧非线性系统。表2所列的计算结果显示,对粗糙接触界面,其力-变形关系的刚度指数均为α>1,因而,粗糙界面接触振动的响应特性具有软弹簧非线性系统的动力学特征。
3.3.2 对数衰减特性
采用式(8)计算不同刚度模型自由振动曲线的等效阻尼比随振幅UN的变化曲线,如图10所示。其中,UN=Ui/U1(i=1,2,3,…)。图10显示,仅刚度指数为α=1的线性系统的阻尼比保持计算值ζ=0.005不变,其他刚度指数对应的等效阻尼比均随着振幅的减小而递减。同时可以看出,对线性系统,可以采用对数衰减公式估算其阻尼比[18];但是对非线性刚度系统而言,即使系统具有线性的阻尼特性,采用对数衰减公式估算获得的系统阻尼比仍然与振幅相关。因而,对瞬时频率随振幅变化的非线性系统,对数衰减公式并不适用于估算其阻尼比。
3.3.3 能量耗散特性
基于获得的接触力-变形关系式(15),式(13)所示的系统输入能量可以表示为:
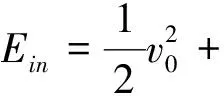
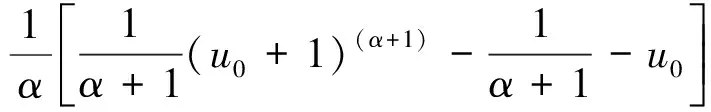
(18)
采用式(12),式(14)和式(18)计算不同刚度模型自由振动响应每周期的能量耗散率和累积能量耗散率,如图11所示。图11显示,对不同指数的接触刚度模型(表面形貌),每周期的能量耗散率均随着时间逐渐减小为0,而累积能量耗散率则逐渐增大到1;当无量纲时间τ≈600时,ND=0,NSD=1,即τ≈600时的累积能量耗散量达到系统的输入能量。图11同时显示,对不同指数的接触模型,其能量耗散率随时间变化基本完全相同,该结果表明界面法向振动的能量耗散量很小,其值基本不随刚度模型(表面形貌)的变化而变化。该计算结果与实验研究观测获得的并无明显法向微动能量耗散的结论一致,从理论上验证了文献[6]的实验结果。
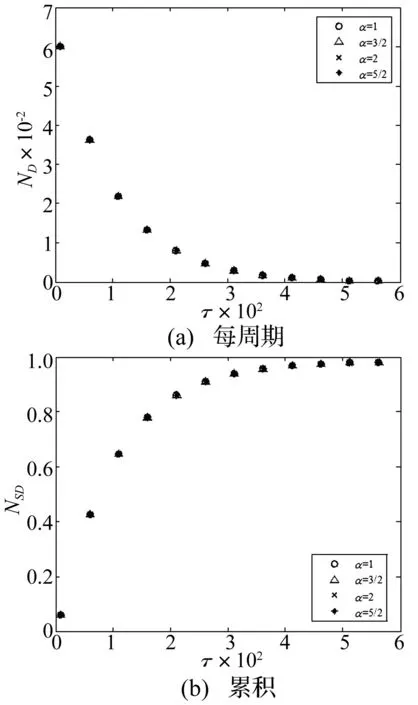
图11 不同接触刚度模型对应的能量耗散率随时间变化曲线
4 结 论
本文建立了粗糙界面法向接触振动模型,提出了计算其法向接触振动的动力学响应特征量和能量耗散量的计算方法。针对具有不同表面形貌的粗糙界面,基于自相似和尺度独立的粗糙表面分形模型,对接触振动过程中,界面接触力-变形关系、接触振动系统的动力学响应特征以及振动能量耗散特性进行了研究,并与Hertz接触模型进行了对比,主要结论如下:
(1)本文的计算结果从理论上解释了界面法向微动能量耗散的实验结果,并进一步验证了提出的界面接触振动模型和计算方法是有效的。
(2)不同表面形貌粗糙界面的弹性接触力-变形关系可以用指数函数关系表示。指数函数指数α的范围为α>1,与Hertz接触理论的α=3/2有所差异;指数大小由表面形貌决定,粗糙度较大的界面具有较大的α值。
(3)不同表面形貌粗糙界面法向微动的动力学响应特征量(瞬时频率,对数衰减)存在较大差异,但是能量耗散特性却基本相同。
参 考 文 献
[1]Smith J D.Transmission of Smith shocks through rolling bearings [J].Journal of Sound and Vibration,1995,181(1):1-6.
[2]温诗铸,黄 平,等.界面科学与技术[M].北京: 清华大学出版社,2011.
[3]Berger E J.Friction modelling for dynamic system simulation [J].ASME Applied Mechanics Review,2002,55(6): 535-577.
[4]Gaul L,Nitsche R.The role of friction in mechanical joints [J].ASME Applied Mechanics Review,2001,54(2): 93-105.
[5]Ferri A A.Friction damping and isolation systems [J].ASME Journal of Vibration and Acoustics,1995,117B: 196-206.
[6]Andrew C,Cockburnt J A,Waring A E.Metal surfaces in contact under normal forces: some dynamic stiffness and damping characteristics [C].Proceedings of the Institution of Mechanical Engineers,Conference Proceedings,1967,182: 92-100.
[7]Johnson K L.Contact mechanics [M].Cambridge University Press,1985.
[8]Nayak P R.Some aspects of surface roughness measurement [J].Wear,1973,26:165-174.
[9]Al-Kindi G,Shirinzadeh B.An evaluation of surface roughness parameters measurement using vision-based data [J].International Journal of Machine Tools and Manufacture,2007,47: 697-708.
[10]Sabot J,Krempf P,Janolin C.Non-linear vibrations of a sphere-plane contact excited by a normal load [J].Journal of Sound and Vibration,1998,214: 359-375.
[11]Rigaud E,Perret-Liaudet J.Experiments and numerical results on non-linear vibrations of an impacting Hertzian contact.Part 1: harmonic excitation [J].Journal of Sound and Vibration,2003,265: 289-307.
[12]Xiao H F,Brennan M J,Shao Y M.On the undamped free vibration of a mass interacting with a Hertzian contact stiffness [J].Mechanics Research Communications,2011,38: 560-564.
[13]邵毅敏,肖会芳.动力系统非连续单一叠加结构界面变形与能量损耗特性[J].振动与冲击,2011,30(4):217-222.
SHAO Yi-min,XIAO Hui-fang.Deformation and energy loss of single layered and discontinuous structural interface of a power system [J].Journal of Shock and Vibration,2011,30(4):217-222.
[14]Sherif H A.Parameters affecting contact stiffness of nominally flat surfaces [J].Wear,1991,145: 113-121.
[15]Yan W,Komvopoulos K.Contact analysis of elastic-plastic fractal surfaces [J].Journal of Applied Physics,1998,84: 3617-3624.
[16]肖会芳,邵毅敏,周晓君.非连续粗糙多界面接触变形和能量损耗特性研究[J].振动与冲击,2012,31(6): 83-89.
XIAO Hui-fang,SHAO Yi-min,ZHOU Xiao-jun.Contact deformation and energy dissipation characteristics of a discontinuous rough multi-interface [J].Journal of Shock and Vibration,2012,31(6): 83-89.
[17]Nayfeh A H,Mook D T.Nonlinear Oscillations [M].Wiley,New York,1979.
[18]Rayleigh J.The theory of sound,Vol.I [M].New York,reprinted by Dover,1945.
