计及减振器非线性阻尼的自行火炮车体振动试验及数值模拟
2014-09-05曹广群王建中朵英贤曾志银
曹广群, 王建中, 朵英贤, 曾志银
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.中北大学 机电学院,太原 030051;3 西北机电工程研究所,咸阳 712099)
在轮式自行火炮射击时车体振动响应分析过程中悬挂系统起着举足轻重的作用,而减振器作为悬挂系统的主要阻尼元件,其动态阻尼特性对悬挂系统特性、整车[1-2]及整个武器系统的动力学响应具有很大影响。
国内外学者对悬挂及减振器特性进行了大量的研究。Besinger等[3]建立了重型车辆悬架减振器模型,Lee等[4-5]建立了能展示减振器特性又较为简明的模型,但是作为试探性研究这些模型仅适应于减振器低频运动工况,不适合本文研究对象的特点。丁法乾等[6]对履带式装甲车辆悬挂系统动力学进行了研究,推导了履带式车辆的减振器阻尼系数表达式及等效悬挂的阻尼系数表达式。申国太等[7]对履带式自行火炮悬挂装置的等效问题进行了讨论,分析了射击时悬挂的受力,给出了车体及悬挂的动力学方程,为进一步分析车体对弹丸的运动提供了基础。叶全勇等[8]根据我国汽车减振器国产化进程中的生产和科研实践,在悬架减振器外特性模拟的基础上,通过线性等效的方法,用分段线性设计去近似等效非线性特性,并通过等效特征参数将分段线性规律量化。王蕾等[9]以对悬挂式弹簧系统为研究对象,通过建立矩形脉冲激励下系统非线性动力学方程,研究该系统冲击特性。庞辉等[10]对某重载卡车的悬挂刚度及阻尼之间的匹配和优化进行仿真和试验研究,为其他车辆悬架参数优化设计提供参考。可见,对悬挂及减振器非线性阻尼特性研究多针对履带式自行火炮或者车辆开展,就轮式自行火炮悬挂系统及减振器非线性阻尼特性对整车响应规律的研究开展较少。
对于筒式减振器建模仿真方面,目前多采用参数化模型。参数化模型有两种建模方法,一种是考虑减振器内部油液的流动及节流阀元件的真实的工作状态,考虑结构和流体的耦合,此为物理参数模型;另一种方法是将减振器抽象为一些具有某种力学特性的典型的物理元件的组合,建立等效的力学特性分析模型,称为等效参数模型[11]。筒式减振器在实际工作中压缩和拉伸行程的阻尼特性是不一样的,而目前仿真中对筒式减振器多采用线性弹簧和线性阻尼来代替,压缩和拉伸行程中刚度和阻尼系数相同,这显然与实际物理过程不符。本文采用等效参数模型和物理参数模型结合的方式,对某轮式自行火炮独立式悬挂装置的非线性阻尼及刚度进行了建模与仿真,为某轮式自行火炮连发射击响应分析奠定基础。
1 构造原理及阻尼特性表达式推导
某轮式自行火炮采用了筒式双作用式液压减振器,在拉伸和压缩行程都产生阻尼。减振器安装在下摆臂的上方,上端固定在车体的侧甲板上,下端与下摆臂铰接。带杆的活塞在充满液体的封闭缸筒内运动,迫使液体通过活塞上的节流孔流动,从而产生阻尼力。
1.1 减振器结构及工作原理
某轮式自行火炮采用的减振器结构如图1所示。减振器内部由工作腔和补偿室两部分组成。工作腔4下部为底阀3,底阀3上有常通孔及两个单向限压阀;中间有带杆的活塞6,工作腔的上端安装有活塞杆导向座7及密封装置8。活塞6上有常通孔及两个单向限压阀,每个方向各一个,与底阀3的常通孔及阀门配合,控制工作压力及各个方向的流量,并使工作腔4内不产生气泡、充满液体。补偿室5内上部为空气,下部为工作液,通过底阀与工作腔连通,在活塞杆10进出工作腔4时,接纳和提供需要调节的液体,它还可以补偿由于温度造成的液体容积的变化。补偿室5上端与导向座出口相连,使活塞杆的油封处于低压状态。

1.下连接环;2.外筒;3.底阀;4.工作腔;5.补偿室;6.活塞;7.活塞杆导向座;8.密封装置;9.端盖;10.活塞杆;11.上连接环
1.2 阻尼特性参数表达式推导
1.2.1 拉伸行程阻尼力计算
(1)
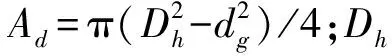
1.2.2 压缩行程阻尼力计算
基于连续性定理及液压相关理论,推导得出压缩行程的减振器阻尼力为:
(2)
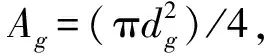

1.2.3 阻尼系数的计算

(3)
(4)
1.3 减振器在悬挂上的等效阻尼刚度系数换算
由于减振器不是直接安装在轮胎轮轴垂直上方,因此轮胎轮轴垂直方向的运动速度和悬挂阻尼并不相等,两者需要通过功率相等的原理进行换算。
(5)
设传动比:
(6)
则:
FS=iFZ
(7)

所以:
(8)
对悬挂阻尼力FS求全微分得:
(9)
式中:c为减振器在悬挂上产生的阻尼系数;k为减振器在悬挂上产生的刚度系数。
因此,由减振器在悬挂上产生阻尼系数c为:
(10)
由减振器在悬挂上产生的刚度系数k为:
(11)
式(10)、(11)中未知量只有i、 di/dy,下面对其进行求解。

图2 减振器及车体连接几何关系
A点是减振器的上铰链点中心,坐标设为(xA,yA),B点是减振器的下铰链点;O点是下摆臂枢连车体的回转轴中心,减振器下连接臂长度为lOB,减振器轴心线AB,长度为lAB;减振器轴心线与连接臂之间的夹角为α;连接臂与水平线的夹角为β,下摆臂与水平线夹角为γ,具体几何关系如图2所示。
从图2中几何关系,经过几何推导可以得出:
(12)
(13)
将式(12)、式(13)代入式(10)可得减振器在悬挂上的等效阻尼系数为:
(14)
将减振器拉伸行程阻尼系数clz代入式(14)并整理得悬挂拉伸行程等效阻尼系数cl为:
(15)
将减振器压缩行程阻尼系数cyz代入式(14)并整理得悬挂压缩行程等效阻尼系数cy为:
(16)
将式(13)和式(1)代入式(11)整理可得拉伸行程减振器在悬挂上的等效刚度系数为:
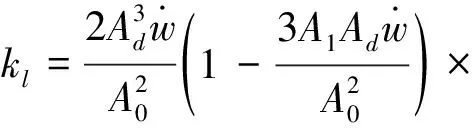

(17)
将式(13)和式(2)代入式(11)整理可得压缩行程减振器在悬挂上的等效刚度系数为:


(18)
2 轮式自行火炮连发射击数值模拟及试验
2.1 连发射击车体振动数值模拟计算
某轮式自行火炮为小口径自动炮,射击方式包括单发射击和连发射击。单发射击状态,后一发弹丸出炮口时,炮口已经完全恢复到静止状态,其射击精度不受前一发的影响。连发射击时,弹丸始终在炮口振动中射出,炮口振动对弹丸出炮口瞬间的运动姿态产生影响,进而影响火炮射击密集度和射弹散布。通过实弹射击试验发现,对于连发射击出现射弹散布不断变大、射击精度明显降低的现象,有必要研究连发射击时振动规律。而悬挂系统的阻尼特性是该轮式自行火炮全炮动力学响应的主要影响参数之一[6],本文针对悬挂系统中减振器采用非线性参数及线性参数两种情况下轮式自行火炮连发射击时的动力学响应进行数值模拟计算,并通过实弹试验测试进行验证。
轮式自行高炮连发射击动态响应数值模拟时,首先需要建立该炮数值模拟模型。模型基于该自行火炮物理样机建立,主要包括回转部分和底盘部分。回转部分包含炮塔壳体、摇架、供输弹机构、高低机、平衡机、身管、雷达、光电等;底盘部分包括车体总成(含发动机、弹药、下座圈等)、悬挂系统,其中悬挂系统包括下摆臂、轮毂、圆柱螺旋弹簧、减振器、轮胎等。悬挂系统参数方面,圆柱螺旋弹簧刚度阻尼由试验测试值给定;轮胎采用ADAMS中轮胎模型,其轮胎半径、轮胎宽度、摩擦系数、垂直刚度、垂直阻尼、纵向滑移刚度、外倾刚度、侧倾刚度值由试验测试给出;减振器的非线性刚度及阻尼系数表达式由上节推导得出。悬挂系统按照物理样机的拓扑关系建立。
采用三维绘图软件UG建立轮式自行火炮的几何模型,将建立的模型导入到动力学分析软件ADAMS中,通过添加几何约束和施加载荷构建数值模拟计算模型,如图3所示。在此计算模型上对该轮式自行火炮连发射击时车体的动力学特性进行研究。

图3 轮式自行火炮数值模拟计算模型
在边界条件和射击载荷完全相同的情况下,对某轮式自行火炮在以下两种情况下的十连发射击进行了数值模拟计算:第一种情况减振器采用线性阻尼及刚度系数,阻尼及刚度系数通过减振器压缩和拉伸行程阻尼力的平均值计算得出;第二种情况减振器刚度及阻尼系数采用本文推导获得的非线性阻尼及刚度系数表达式描述。由推导结果可见,减振器非线性刚度、阻尼系数表达式在拉伸和压缩行程中不同,而在ADAMS软件中只能用一个函数表达式对它们进行赋值,因此,需要将拉伸和压缩行程两个表达式统一起来。减振器的悬挂等效阻尼系数表达式f(c)可统一为:
f(c)=f(cy)·{SIGN[0.5,VARVAL(VZ)]+0.5}
-f(cl)·{SIGN[0.5,VARVAL(VZ)]-0.5)}
(19)
减振器的悬挂等效刚度系数表达式f(k)可统一为:
f(k)=f(ky)·{SIGN[0.5,VARVAL(VZ)]+0.5}
-f(kl)·{SIGN[0.5,VARVAL(VZ)]-0.5}
(20)
其中:f(cl)、f(cy)、f(kl)、f(ky)分别为上文推导的表达式(15)、(16)、(17)、(18);
VZ为轮胎相对于车体的速度矢量;
VARVAL(VZ)为状态参量VZ当前值;
SIGN(a,b)为符号函数,
当b≥0SIGN(a,b)=ABS(a),否则
SIGN(a,b)=-ABS(a)
可见,压缩行程中VARVAL(VZ)≥0,
f(c)=f(cy),f(k)=f(ky)
拉伸行程中VARVAL(VZ)<0,
f(c)=f(cl),f(k)=f(kl)
2.2 连发射击车体振动试验测试
为了获取连发射击时车体振动的相关参数,在靶场进行了十连发实弹射击试验及测试。
2.2.1 测试仪器及原理
测试试验所用的测试仪器主要有:多维动态位移测量仪和数据采集仪。

图4 实弹射击时车体前测点

图5 实弹射击时车体后测点
图4和图5分别是自行火炮射击试验时车体振动前测点和后测点的试验现场。图中所示测试仪器为多维动态位移测量仪,该测试仪由三角支架、位移传感器组件和套筒等组成。该仪器可以测量测点面内运动位移的时域曲线。测试前,在自行火炮车体侧面前后各选择一个测点,将两个套筒分别固定在测点上;套筒上有用于连接测量杆的孔,测量杆可沿该孔相对套筒滑动;测量杆的下端连接位移传感器,并与外侧放置的三角支架固连,三角支架固定在地面上。
火炮射击时,套筒随自行火炮车体同步运动,从而使得测量杆既可以沿套筒上的孔相对滑动,也能够绕三角支架连接点相对转动。通过数据采集系统采集位移传感器的数据即可测量出自行火炮车体测点相对于角位移传感器旋转中心的线位移和角位移。根据该测试结果,应用专用处理软件即可给出车体测点相对于大地的高低及水平位移随时间变化规律。
2.2.2 测试状态
实弹射击试验状态为:方位角为180°(即反向射击),高低角为0°,十连发射击;射击采用全装药炮弹,炮塔方位角机械锁死,车体悬挂闭锁。两测点均布置在射击平面右侧,前测点为靠近车首部分的测点,后测点为靠近车尾部分的测点。
3 结果及分析
轮式自行火炮在十连发反向射击时,减振器采用线性和非线性参数数值计算及试验测试结果如表1、图6、图7所示。

表1 数值模拟与测试结果

图6 车体前测点振动位移曲线
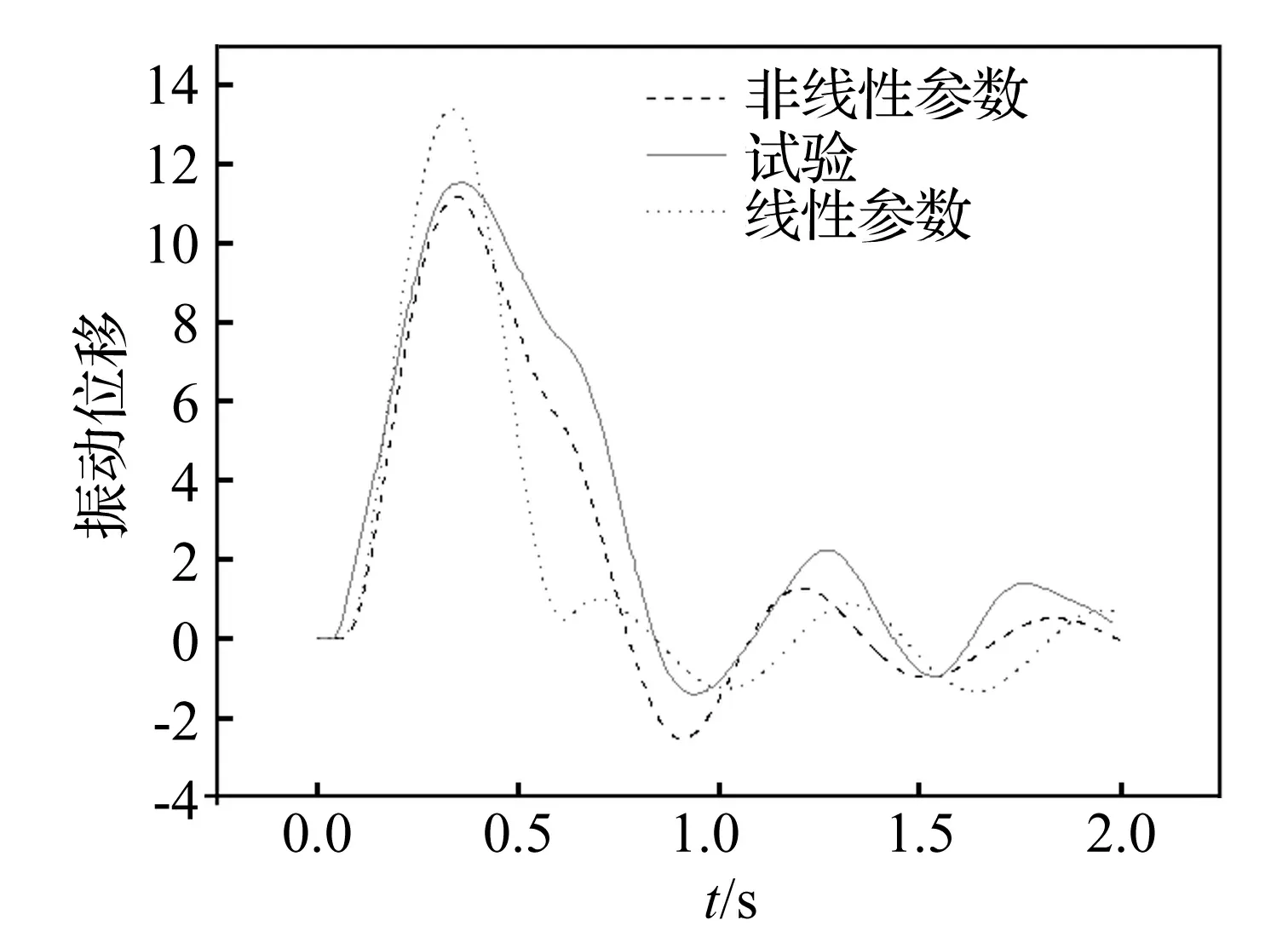
图7 车体后测点振动位移曲线
从表1、图6、图7可以看出,采用线性阻尼及刚度系数仿真时,前测点及后测点的曲线变化规律与实测曲线差别很大,前、后测点最大位移值差值较大,最小值虽然差值较小,但是出现的时间点为第二个波谷;而采用非线性阻尼及刚度系数仿真时,前、后测点曲线与实测曲线规律吻合良好,前、后测点的最大位移与实测值差值都较小。
4 结 论
针对某轮式自行火炮悬挂系统减振器的阻尼特性对连发射击时车体振动的影响问题,基于建立的该轮式自行火炮的数值模拟模型,对减振器采用线性参数和推导的非线性参数表达式两种情况下的车体动态响应进行了数值模拟,并对连发射击时车体两个测点振动位移进行了测试,数值模拟与测试结果表明:采用非线性参数动力学仿真结果优于线性参数,减振器有必要采用接近物理实际的非线性表达式来进行数值模拟计算。本文所推导减振器非线性参数表达式可为研究该轮式自行火炮连发射击时炮口振动奠定基础,并为该炮射击精度分析预测提供参考。
参 考 文 献
[1]Simms A,Rolla D.The influence of damper properties on vehicle dynamic behavior [J].Society of Automotive Engineering,2002,1:79-86.
[2]Duym S W R.Simulation tools,modeling and identification,for an automotive shock absorber in the context of vehicle dynamics [J].International Journal of Vehicle Mechanics and Mobility,2000,33(4):261-285.
[3]Besinger F H,Cebon D,Cole D J.Damper models for heavy vehicle-ride dynamics[J].Vehicle System Dynamics,1995,24(1):35-64.
[4]Lee K.Numerical modeling for the hydraulic performance prediction of automotive monotube dampers [J].Vehicle System Dynamics,1997,28:25-39.
[5]徐中明,李仕生,张志飞,等.汽车减振器外特性仿真与试验分析[J].振动与冲击,2011,30(8):92-96.
XU Zhong-ming,LI Shi-sheng,ZHANG Zhi-fei,et al.Outer characteristics simulation and experimental analysis of automotive shock absorbers [J].Journal of Vibration and Shock,2011,30(8):92-96.
[6]丁法乾.履带式装甲车辆悬挂系统动力学[M].北京:国防工业出版社,2004:5.
[7]申国太,苗会龙,赵子华,等.自行火炮射击时车体运动分析[J].弹道学报,1993,4:50-55.
SHEN Guo-tai,MIAO Hui-long,ZHAO Zi-hua,et al.Analysis of chassis movement when self-propelled gun firing [J].Journal of Ballistics,1993,4:50-55.
[8]叶全勇,俞德孚.车辆悬架减振器外特性非线性的等效线性计算[J].兵工学报(坦克装甲车与发动机分册),1994,53:22-29.
YE Quan-yong,YU De-fu.Equivalent linearized calculation of the nonlinear outer performance of shock absorbers [J].Acta ArmamentarII (Fascicule of Tank Panzer and Engine),1994,53:22-29.
[9]王 蕾,陈安军.矩形脉冲激励下悬挂式弹簧系统冲击特性的研究[J].振动与冲击,2012,31(11):142-144.
WANG Lei,CHEN An-jun.Shock characteristics of a suspension spring system under action of a rectangular pulse [J].Journal of Vibration and Shock,2012,31(11): 142-144.
[10]庞 辉,方宗德,李红艳,等.某载重卡车悬架参数优化及试验研究[J].振动与冲击,2012,31(8):92-95,106.
PANG Hui,FANG Zong-de,LI Hong-yan,et al.Optimization and test for suspension parameters of a heavy-duty [J].Journal of Vibration and Shock,2012,31(8):92-95,106.
[11]赵 亮.车辆悬架系统中新减振元件设计和减振控制算法研究[D].长沙:湖南大学,2008:4-8.
