结构振动阻尼测试的衰减法研究
2014-09-05尹帮辉王敏庆吴晓东
尹帮辉,王敏庆,吴晓东
(西北工业大学 航海学院,西安 710072)
阻尼处理技术是振动噪声控制的一项重要手段,广泛应用于航天、航海等领域,例如潜艇的阻尼瓦等。为了能够较为准确的预测阻尼结构的振动响应,通常需要使用有限元、统计能量分析[1]等数值计算方法对实际振动系统进行建模,而这些模型都需要输入阻尼参数。由于实际结构中阻尼产生机理的复杂性,比如潜艇阻尼瓦材料的阻尼对海水温度变化很敏感,从理论上预测阻尼结构的阻尼在很多情况下很困难,因此一般都需要通过实验方法对阻尼参数进行测量,常用的测量方法有功率输入法和衰减法等。输入功率法[2-4]利用振动系统在激励作用下的输入功率和振动能量来计算损耗因子,该方法是伴随统计能量分析理论的发展而引入的测试方法,它直接使用统计能量分析的概念,所以测试结果反映了统计能量分析意义下的频段阻尼,但是由于该方法实验设备的安装比较复杂,同时需准确测量输入功率,对实验精度要求比较严格,并且只能用于测量均质试件,因此其使用受到很大的限制。衰减法[5-9]利用振动系统在自由振动下的衰减特性通过带通滤波等技术来获取频段平均阻尼特性,该方法很早就用于阻尼测试[11-12],在标准ASTM C423和ISO 3382-1:2009中也有所涉及,由于其测试方法简单,在机械振动以及建筑声学中广泛使用,但是由于理论以及测试方法本身的局限以及问题本身的复杂性使得衰减法测试的精度不高,一般在一个数量级内变化的测试结果都会被认可,本文针对衰减法在阻尼测试中遇到的一些问题及测量误差产生的具体原因,使用理论与数值仿真的方法进行分析研究,为进一步提高测量精度提供一定的帮助。
当频段内含有多阶模态时,一般情况下各阶模态的阻尼会有一定差异,这会导致能级衰减曲线出现分段现象[7-9],这时如何确定频段平均阻尼一直是阻尼测试中的一个难题,而这对于统计能量分析具有重要的意义。Wu等[7,9]使用实验分析方法通过能级衰减曲线初始衰减率计算得到了频段阻尼,该阻尼同统计能量分析意义下的频段阻尼一致,而Bies等[1,10]则发现衰减法测试结果小于稳态法测试结果即统计能量分析意义下的频段阻尼。本文使用理论和仿真方法对这些结论进行了进一步的研究,给出了其适用范围。另外当频段内含一阶模态或不含模态时,其频段阻尼结果对于统计能量分析意义不大,但是仍然可用于有限元分析,为其提供阻尼参数,所以本文也讨论这两种情况下的阻尼测试。
在使用衰减法进行频段阻尼测试时,首先将某一1/3倍频程频段的信号分量提取出来,这主要有两种方法:FFT技术和数字滤波器法[13],在两种方法中都存在频段外模态的能量泄露影响频段阻尼测试结果的现象,目前对这个问题的研究还比较少,本文对数字滤波器法中的能量泄露问题进行了讨论。
最后本文使用平板的瞬态冲击有限元仿真数据对前面两个问题进行进一步的研究,对相关结论进行了验证。
1 测试系统
衰减法主要是利用振动系统在自由振动中其能级随时间的推移而衰减的规律进行阻尼测量,根据其能级衰减率可以计算各种阻尼参数,其测试系统原理图如图1所示。使用衰减法进行阻尼测量:首先使用数字滤波器对采集得到的振动信号进行滤波,从而得到某一频段的振动信号;然后对滤波后的某一频段内的信号进行反向积分得到能级衰减曲线;改变激励点/测点反复进行至少50次测试,对所有的能级衰减曲线求平均;最后根据平均能级衰减曲线进行初始衰减率的拟合从而得到频段衰减率。

图1 测试系统原理图
衰减法测量中振动系统的激励方式主要有两种,即随机激励法[7]和脉冲激励法[9]。随机激励法使用随机载荷对振动系统进行激励,等系统稳定后突然关掉电源,根据之后的能级衰减进行阻尼测量,这种方法的初始衰减点的确定比较困难[7],同时需要安装激振设备,适用范围受到很大的限制;脉冲激励法使用冲击载荷对被测试件激励,适用范围较广,对于舰船上常用到的水下阻尼测量等情况目前只能使用冲击激励法。本文主要对冲击激励法进行研究。
本文使用6阶巴特沃斯滤波器进行带通滤波,但是当使用其对大阻尼系统进行测量时,由于滤波器本身的阻尼特性常常干扰测试结果, Jacobsen[5]提出反向滤波技术可以将能测试的阻尼上限大大提高,该方法在滤波之前先将信号进行反向,滤波之后再对滤波后信号进行反向。
由于振动系统在某一频段通常由很多模态组成,这使得冲击响应的能级衰减曲线振荡,呈现出“拍”现象[11],为了平滑衰减曲线, Schroeder[6]提出反向积分方法以解决该问题。
为了隔离频段外模态的影响、反映统计能量分析的能量均分假设并且进一步平滑能量衰减曲线,需要对不同激励点和测点的测试数据的多条能级衰减曲线做平均,标准ASTM C423规定至少需要使用50个数据作平均。
在统计能量分析中一般使用损耗因子η来描述频段阻尼,由于在本文中使用能级衰减率γ能够比较直观的判断误差来源(见第3节),并且损耗因子一般也是根据能级衰减率计算得到,所以本文使用能级衰减率作为阻尼描述参数,二者具有如下的转换关系[12]:
γ=27.3fη
(1)
对于脉冲激励下的振动系统,在某测点的振动响应通常可以表示为各阶模态的叠加,可以表示为以下的形式:
(2)
其中,fi为第i阶模态的固有频率;ηi为第i阶模态的模态损耗因子;Ai为第i阶模态的位移振幅,反映了该模态在冲击完毕时在该测点的初始能量。下面第2节和第3节中使用这种标准信号对频段内含多模态的频段衰减率以及频段外模态对阻尼测试结果的影响进行分析。
2 频段内含多模态的频段衰减率
对于频段内含有多阶模态的情况,其能级衰减曲线分段现象比较常见,这时对频段衰减率的判定存在很大争议,瞬态方法和稳态方法测试结果存在不一致性,这些问题至今尚未完全解决。下面先从理论上研究衰减法测试结果与统计能量分析意义下的频段阻尼之间的关系。
如果一个频段中含多阶模态,其统计能量分析意义下的频段损耗因子表示在稳态激振下一个周期振动中损耗的能量和系统振动的机械能的比[14],反映了各阶模态的平均耗能特性。当模态阻尼不是很大的时候,激励的输入功率等于各模态的输入功率的和,系统的机械能等于各模态的机械能的和。统计能量分析理论的一个基本假设是能量均匀分布假设,对于在某一特定激励点激励时该假设一般不成立,但是若对很多激励点的测试结果做平均后,则可以近似看做能量均分。使用能量均分假设,经过化简,统计能量分析意义下的损耗因子可以表示为:
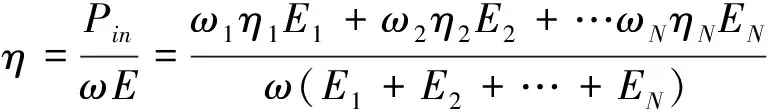


(3)
其中Pm表示输入功率,ω表示频段的中心角频率,E为稳态振动能量,Ei、ηi、ωi分别表示第i阶模态的机械能、模态损耗因子以及固有角频率,N为频段内的模态阶数,由于ωi和ω位于同一个频段内,其比值通常接近于1,所以上式约掉了ωi和ω。上式表明:统计能量分析意义下的频段损耗因子近似等于各模态的损耗因子的算术平均值,亦即频段衰减率近似等于各模态衰减率的平均值。
振动系统在冲击激励下的能级衰减曲线与冲击激励起来的各模态的初始能量和各阶模态的模态衰减率有关系。对于某一特定的激励点/响应点,测试信号反映的各模态的初始能量一般不相同,模态振型峰值附近的激励点/响应点的初始能量大,节点/节线附近的激励点/响应点的初始能量小,但是当取很多激励点/响应点的能级衰减曲线做平均时,各模态的初始能量大致相等,在这种情况下振动系统的能级衰减率可简化为:
(4)
其中Em,γm、ωm、ξm分别表示第m阶模态的初始能量、模态衰减率、固有角频率和模态阻尼比,N为该频段中所含的模态数目,γmin表示该频段中阻尼最小模态的模态衰减率。根据式(3)和式(4)可以看出:衰减法中的初始衰减率接近统计能量分析意义下的频段衰减率;当衰减时间比较长的时候,其衰减率接近频段中阻尼最小模态的模态衰减率。
下面对上一段推论中用到的初始能量均分假设做推导。对于在x0处施加冲量为I的冲击载荷的振动系统,其在测点x处的位移可表示为:
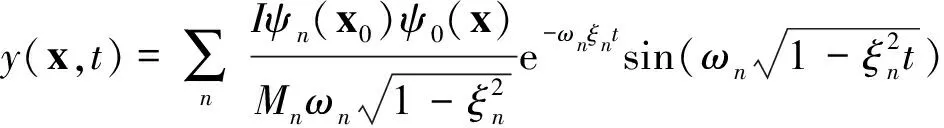

(5)
其中:ψn,Mn、ωn、ξn表示第n阶模态的模态振型、模态质量、固有角频率、模态阻尼比。测点信号初始能量的第n阶模态分量对于大量冲击点/测点的平均值可以表示为式(6),其中ω为频段的中心频率。对于四边简支边界条件,式(6)为一常数,同模态的阶数没有关系,所以同频段各阶模态的能量基本相等。对于固支和自由边界条件,使用有限元模态分析也可以验证得到各模态的能量基本相等的结论。
(6)
以上从理论上推导了使用初始衰减率来测量频段衰减率的原因, Wu等[7,9]也根据实验对其进行了验证,并且指出了传统的根据能级下降60dB或者25dB(标准ASTM C423)来测量得到的阻尼会小于真实的阻尼值的原因正是由于没有采用初始衰减率。但是Bies等[1,10]在实验中却发现即使使用初始衰减率测得的阻尼值仍然小于统计能量分析意义下的阻尼值。下面使用式(2)描述的标准信号以及图1表示的测试系统对这个问题进行研究。
考虑下面的二自由度系统:模态振幅A1=A2=1 mm;模态频率f1=950 Hz、f2=1 050 Hz,改变各模态的模态衰减率,研究中心频率为1 000 Hz的1/3倍频程频段的频段衰减率测试,其初始衰减率拟合结果如表1所示。表1中的误差计算公式如下:
(7)
其中,γ为拟合得到的频段衰减率,γi为第i阶模态的模态衰减率。表1中的半衰时间是根据式(4)左侧的等式在某个时刻t1满足
(8)
的情况下得到的。对于只含两阶模态的频段,假设其初始能量相等,对式(8)进行求解可得:
(9)

表1 模态衰减率差别对频段衰减率的影响
从表1可以看出:当频段内各模态的模态衰减率差别不是很大的时候,测试得到的频段衰减率很接近统计能量分析意义下的频段衰减率,即各模态衰减率的平均值,这同前面的理论分析一致;当各模态的模态衰减率相差较大的时候,测试得到的频段衰减率接近阻尼较小的模态的模态衰减率,从而使得测试误差较大,下面对这种现象进行解释:

图2 γ1=100 dB/s,γ2=500 dB/s时的能级衰减曲线
图2作出了相应于表1中γ1=100 dB/s、γ2=500 dB/s时的直接使用给定振动信号计算得到的能级衰减曲线及经过反向积分的能级衰减曲线。从式(9)可以看出:当频段内两阶模态的衰减率相差越大,半衰时间越小,其初始衰减率在开始时刻就会迅速变化。从图2中给定信号的能级衰减曲线的振幅拟合得到的初始频段的衰减率为231 dB/s,这小于初始衰减率300 dB/s而略大于半衰时间点的衰减率200 dB/s,这说明:由于半衰时间过小导致在能级衰减曲线中较难识别出初始衰减率。从图2中经反向积分后的能级衰减曲线可以看出其初始段的衰减率同后面一段曲线的衰减率基本一致,这说明反向积分也是造成测量误差的一个原因。综上所述:当频段内的两阶模态的模态衰减率相差较大时,由于衰减率变化过快以及反向积分的影响导致频段衰减率偏小而接近最小模态衰减率。
3 频段外模态对阻尼测试结果的影响
如果频段中不含任何模态,那么频段外某阶模态的能量泄露将会对该频段的频段衰减率造成影响。考虑单自由度系统:固有频率为f=250 Hz,幅值A=1 mm,模态衰减率γ为70 dB/s或700 dB/s。相应于这两种模态衰减率,表2给出了在250 Hz附近的一些频段的频段衰减率拟合结果,从中可以看出:如果该频段不含任何模态,则频段外模态对该频段的影响只同该模态的衰减率相关,而与频率的位置没有关系。

表2 频段外模态能量泄露所造成的周围频段的衰减率(dB/s)
下面再考虑由于频段外模态的能量泄露而对附近含有模态的频段的频段衰减率所造成的影响。考虑二自由度系统:固有频率为f1=790 Hz、f2=1 000 Hz,模态衰减率:①γ1=100 dB/s、γ2=700 dB/s,或者②γ1=700 dB/s、γ2=100 dB/s,考虑中心频率为1 000 Hz的1/3倍频程频段,第1阶模态位于频段之外,第2阶模态位于频段之中。表3给出了频段外模态幅值变化时,频段衰减率拟合结果的变化情况,从表3中可以看出:当频段外模态的模态衰减率比频段内模态的模态衰减率小很多的时候,随着频段外模态能量的增加,其对频段衰减率将产生显著影响;当频段外模态的模态衰减率比频段内模态的模态衰减率大很多的时候,其对频段衰减率的影响不大。
相应于表3频段外小阻尼情况中A1=1 mm,A2=1 mm的幅值衰减曲线如图3所示。从中可以看出其能级明显分两段,第二段的衰减率为100 dB/s,为频段外模态的模态衰减率。结合表2和图3可以看出:使用衰减率作为阻尼参数相对于衰耗因子能够更容易判断出衰减法中的误差来源。

表3 模态幅值大小分布对频段衰减率的影响
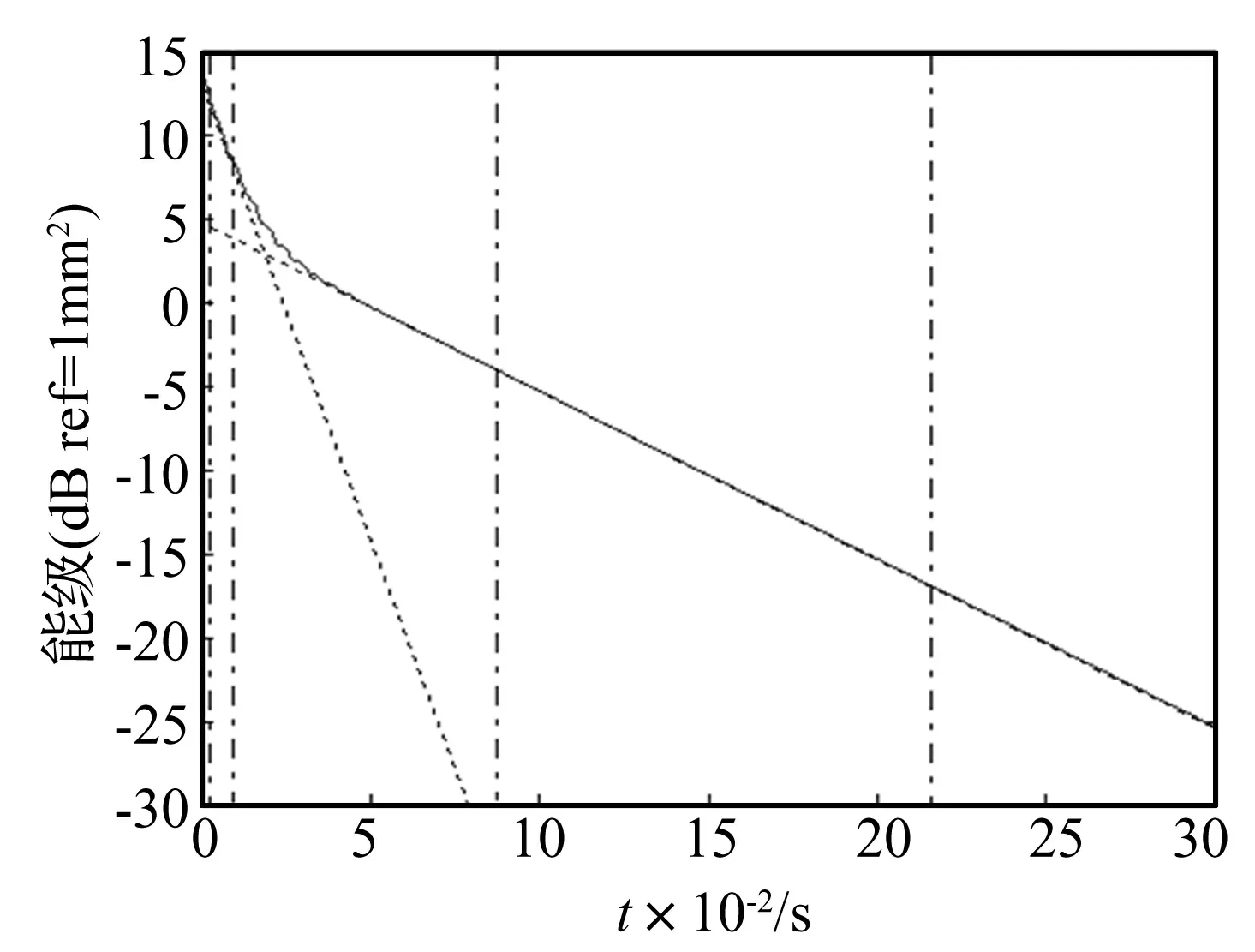
图3 模态衰减率①中当A1=1 mm,A2=1 mm时的能级衰减曲线
下面考虑频段外模态的位置对频段衰减率的影响。取幅值A1=A2=1 mm,衰减率γ1=700 dB/s、γ2=70 dB/s,改变频段外模态频率位置,考虑中心频率为1 000 Hz的1/3倍频程频段的频段衰减率,表4给出了结果,从中可以看出:频段外模态距离某频段越近,其对该频段的衰减率影响越大。

表4 模态频率位置对频段衰减率的影响
综上所述:如果频段中不含任何模态,则频段外模态对该频段的影响只同频段外模态的衰减率相关,而与其频率位置没有关系;如果频段中含有模态,则频段外模态对该频段的影响同频段外模态的衰减率、幅值、频率位置都有关系,衰减率越小影响越大、幅值越大影响越大、越接近该频段影响越大。
4 具体振动系统的衰减法阻尼测试
上面使用标准衰减信号研究了衰减法阻尼测试结果与统计能量分析意义下的频段阻尼之间的关系以及频段外模态的阻尼对频段内阻尼测试结果的影响,下面对一个具体的振动系统使用图1的数据处理系统对前面的相关结论进行验证,其中使用的数据来源于平板在冲击激励下的瞬态衰减响应的ANSYS仿真数据。平板长0.8m、宽0.6m、厚5mm,材料为钢,四条边处施加自由边界条件,使用的冲击载荷如图4所示。

图4 平板上施加的冲击载荷
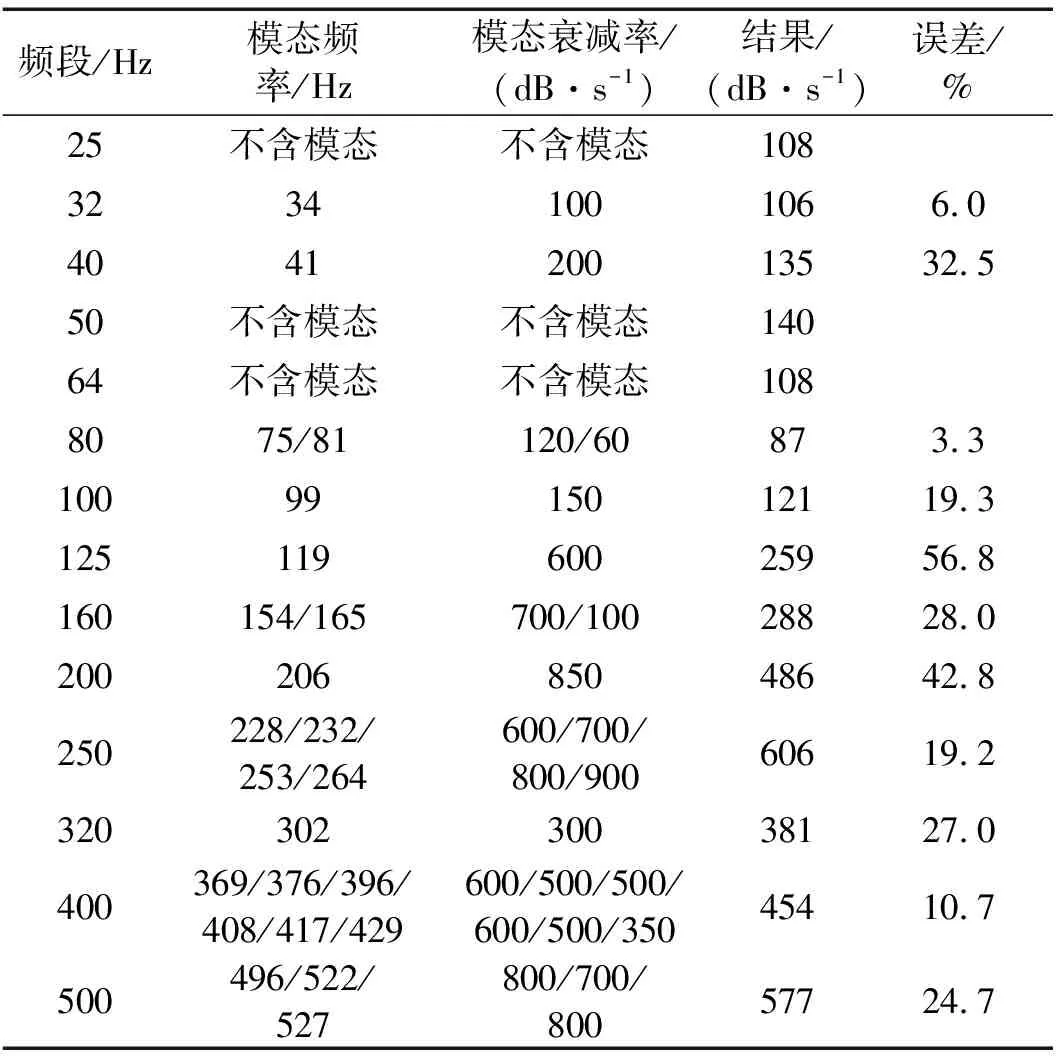
表5 平板各频段所含模态的衰减率及其频段衰减率
为了能获得图1的流程图中的衰减信号,随机选择冲击点和测点作50次瞬响应分析,提取节点处的位移值作为衰减法的输入信号。每次仿真的总时间0.8 s,每一子步之间的时间间隔为0.000 1 s。做瞬响应分析时使用模态叠加法,各模态的模态衰减率如表5所示,另外表5中的频段表示的是1/3倍频程频段。表5的后两列给出了其频段衰减率拟合结果及其误差,后面分频段内不含模态、频段内含一阶模态、频段内含多阶模态三种情况分别对结果进行讨论。
4.1 频段内不含模态
在表5中共有3个频段不含模态,即中心频率分别为25 Hz、50 Hz、64 Hz的1/3倍频程频段。其中中心频率为25 Hz的频段主要受到固有频率为34 Hz的模态的影响。50 Hz的频段主要受到41 Hz和75 Hz的固有频率的影响。64 Hz的频段主要受到75 Hz和81 Hz的影响。这验证了前面的结论:如果频段内不含模态那么该频段的衰减率将主要受频段外靠近该频段的模态的模态衰减率影响。
4.2 频段内含有一阶模态
当频段内仅含一阶模态的时候,测试得到的衰减率应该为这阶模态的模态衰减率,同时受到附近模态的衰减率的影响。表5中共有6个频段仅含一阶模态,即中心频率分别为32 Hz、40 Hz、100 Hz、125 Hz、200 Hz、320 Hz的1/3倍频程频段。其中中心频率为32 Hz、100 Hz的频段的测试误差较小,小于20%;中心频率为40 Hz、 125 Hz、200 Hz的频段由于附近有衰减率较小的模态的影响而偏小;中心频率为320 Hz的频段由于附近有衰减率较大的模态的影响而偏大。图5作出了中心频率125 Hz的频段的能级衰减曲线和初始衰减率拟合曲线,该图存在明显的分段现象,该频段的第二段衰减曲线的衰减率为105 dB/s,这说明了该频段受到衰减率为100 dB/s的模态即频率为165 Hz的模态的影响。
上述讨论验证了前面的结论:当频段附近含有同该频段的衰减率相差较大的模态的时候,该频段的频段衰减会受该模态影响,特别是当频段附近的模态的衰减率远小于频段内的模态的衰减率的时候。

图5 频段125 Hz的能级衰减曲线及初始衰减率拟合
4.3 频段内含有多阶模态
表5中共有5个频段含有多阶模态,即中心频率分别为80 Hz、160 Hz、250 Hz、400 Hz、500 Hz的1/3倍频程频段。中心频率为80 Hz以及160 Hz的频段的能级衰减曲线及初始衰减率的拟合如图6、图7所示,由于80 Hz频段内的两阶模态的衰减率相差不是很大,所以其初始衰减率接近统计能量分析意义下的衰减率,而160 Hz频段内的两阶模态的衰减率相差较大,测试结果更偏向于衰减率较小的模态的衰减率,这验证了第2节中的结论。中心频率为250 Hz、400 Hz、500 Hz的频段由于频段外含衰减率较小的模态,所以频段衰减率偏小。
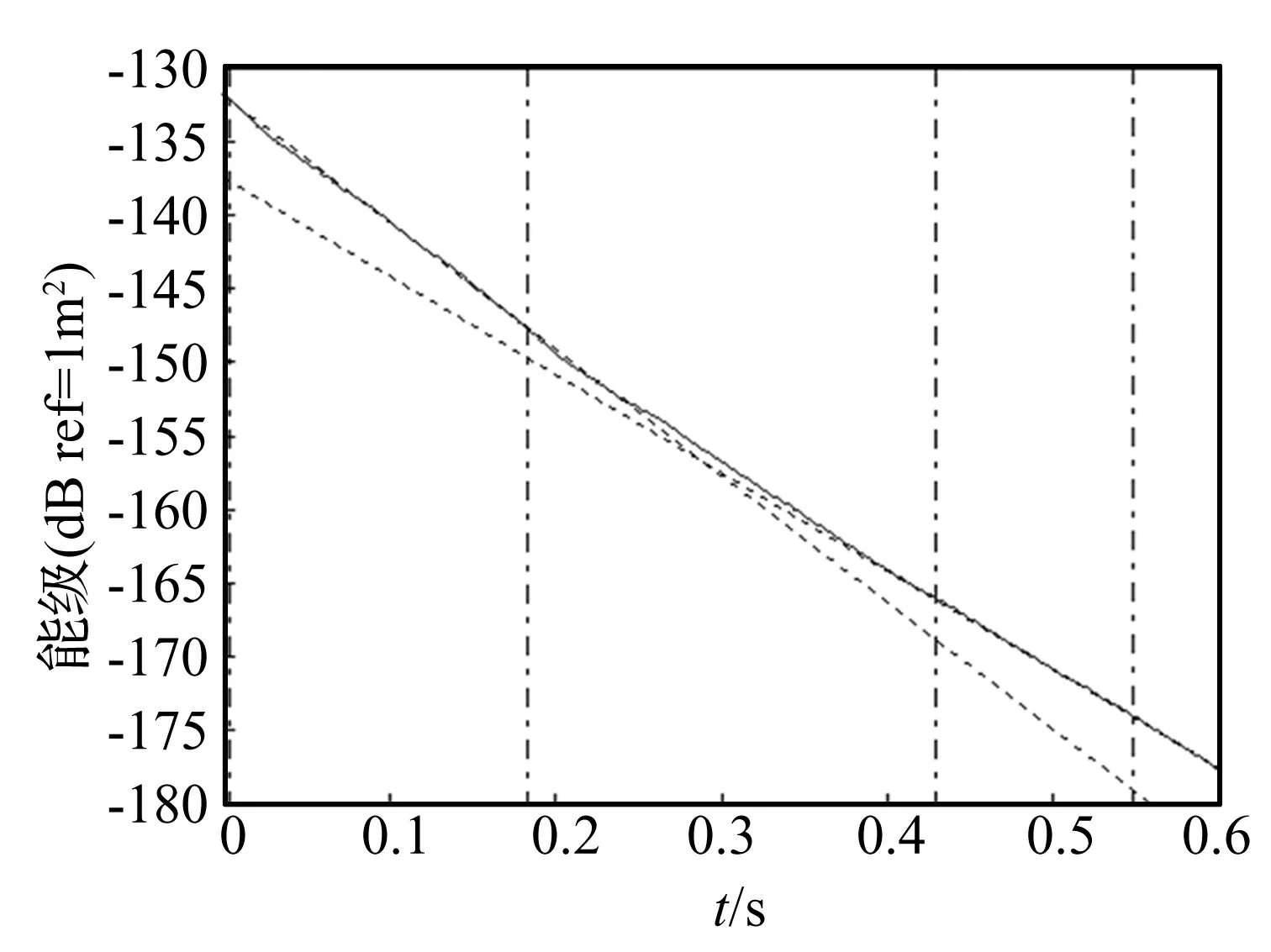
图6 频段80 Hz的能级衰减曲线及初始衰减率拟合

图7 频段160 Hz的能级衰减曲线及初始衰减率拟合
根据前面的讨论发现:如果各模态的衰减率随频率变化平缓,则各频段的衰减率测试结果较为准确;反之,如果各模态的衰减率随频率改变而发生剧烈变化,那么由于频段内大阻尼模态的衰减率难以体现以及频段外模态的能量泄露作用导致相关频段的频段衰减率测试结果误差较大。
5 结 论
(1)当频段内各模态的模态阻尼相差不是很大时,衰减法测试结果同统计能量分析意义下的阻尼值接近;当频段内各模态的阻尼相差较大时,由于衰减率变化过快以及反向积分的原因造成了衰减法测试结果小于统计能量分析意义下的阻尼值;
(2)如果频段中不含任何模态,则频段外模态对该频段的影响只同频段外模态的衰减率相关,而与其频率位置没有关系;如果频段中含有模态,则频段外模态对该频段的影响同频段外模态的衰减率、幅值、频率位置都有关系,衰减率越小影响越大、幅值越大影响越大、越接近该频段影响越大。
(3)如果各模态的衰减率随频率变化平缓,则各频段的衰减率测试结果较为准确;反之,如果各模态的衰减率随频率改变而发生剧烈变化,那么由于频段内大阻尼模态的衰减率难以体现以及频段外模态的能量泄露作用导致相关频段的频段衰减率测试结果误差较大。
参 考 文 献
[1]Lyon R H,Madanik G.Power flow between linearly coupled oscillators[J].The Journal of the Acoustical Society of America,1961,34(5): 623-639.
[2]Bies D A,Hamid S.In situ determination of loss and coupling loss factors by the power injection method[J].Journal of Sound and Vibration,1980,70(2): 187-204.
[3]王敏庆,盛美萍,孙进才.双模态耦合系统的振动耗能特性研究[J].西北工业大学学报,2000,18(4): 553-556.
WANG Min-qing,SHENG Mei-ping,SUN Jin-cai.Theoretical study of vibration energy loss in two-coupled-mode system[J].Journal of Northwestern Polytechnical University,2000,18(4): 553-556.
[4]盛美萍.频带内外模态对频段阻尼特性的影响[J].声学技术,2001,20(2): 56-58.
SHENG Mei-ping.Influence of modes on the damping of frequency band[J].Technical Acoustics,2001,20(2):56-58.
[5]Jacobsen F,Rindel J H.Letters to the editor: time reversed decay measurements[J].Journal of Sound and Vibration,1987,117(1): 187-190.
[6]Schroeder M R.New method of measuring reverberation time[J].The Journal of the Acoustical Society of America,1965,37(3): 409-412.
[7]Wu L,Ågren A,et al.A study of the initial decay rate of two-dimensional vibrating structures in relation to estimates of loss factor[J].Journal of Sound and Vibration,1997,206(5): 663-684.
[8]盛美萍,王敏庆,孙进才.衰减法测定稳态振动系统损耗因子的实验分析技术[J].西北工业大学学报,2001,19(1): 130-135.
SHENG Mei-ping,WANG Min-qing,SUN Jin-cai.On fairly accurately determining the loss factor of two-mode system in steady vibration with the atteniation method[J].Journal of Northwestern Polytechnical University,2001,19(1): 130-135.
[9]Bloss B C,Rao M D.Estimation of frequency-averaged loss factors by the power injection and the impulse response decay methods[J].The Journal of the Acoustical Society of America,2005,117(1): 240-249.
[10]Clarkson B L,Pope R J.Experimental determination of modal densities and loss factors of flat plates and cylinders[J].Journal of Sound and Vibration,1981,77(4): 535-549.
[11]莫尔斯,英格特.理论声学[M].北京: 科学出版社,1984.
[12]Lyon R H.Statistical energy analysis of dynamical system: theory and application[M].The MIT Press,Cambridge,Massachusetts,1975.
[13]Gade S,Herlufsen H.Digital filter vs FFT techniques for damping measurements[R].Br el & Kj r technical review,1994(1).
[14]Ungar E E,Edward J,Kerwin M.Loss factors of viscoelastic systems in terms of energy concepts[J].The Journal of the Acoustical Society of America,1962,34(2): 954-957.
