粘滞阻尼器对空间桁架结构减震作用研究

贾 斌， 罗晓群,2， 丁 娟,3， 张其林

(1.同济大学 土木工程学院,上海 200092； 2.西安建筑科技大学 结构工程与抗震教育部重点实验室,西安 710055；3.精工建筑设计研究总院，上海 200233)

大跨钢结构屋盖广泛用于火车站、会展中心、体育馆、机场候机楼等公共建筑中[1]，具有质量轻、延性好、抗震性能优越等特点。但研究及实际震害表明，地震冲击作用下空间结构部分构件的地震内力可达到或超过静内力，强震作用甚至会导致破坏[2]。空间结构刚度往往较小、整体结构较柔，地震响应有时很大，无法满足舒适度要求，过大位移及加速度响应也会造成构件破坏。因此对大跨空间结构进行减震控制具有重要意义。

目前被动耗能控制技术理论研究及工程应用主要集中于高层建筑及桥梁结构[3-4]，对大跨空间结构减震控制研究主要针对各体系较简单的柱面及球面网壳[5-7],较少涉及复杂的空间桁架结构。空间结构通常采用替换与附加两种方式设置粘滞阻尼器，网架及网壳结构主要以粘滞阻尼器替换原有构件进行减震控制[8-9]。钢管桁架结构因其超静定次数较少，且结构构件主次分明，若采用替换方式会使结构刚度下降影响正常使用乃至安全，因此宜采用附加阻尼器方式。本文针对某体育馆工程，建立上部钢管桁架屋盖与下部混凝土整体结构计算模型，用通用有限元程序进行多维地震波输入的时程分析。以屋盖结构水平向位移、加速度及杆件内力为减震控制目标,研究不同地震波输入时粘滞阻尼器对空间桁架结构的减震控制机理。

1 粘滞阻尼器减震原理

粘滞阻尼器最初为机械工程的消能减震装置，以小型高效特点广泛应用。Constantinou等[10]研制的用于土木工程的粘滞阻尼器作为速度相关型耗能装置，可用一阶Maxwell模型描述其力学行为：

(1)

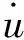
(2)

美国Taylor公司将粘滞阻尼器力学模型表达为：

(3)

式中：C为阻尼系数；sgn( )为符号函数；α为速度指数，α=1时，式(2)与(3)一致，称线性粘滞阻尼；α<1时为非线性粘滞阻尼，阻尼力在速度较小时上升很快，随速度增加阻尼力增长变缓；α>1时称为锁阻尼[12]，与非线性粘滞阻尼相反，阻尼力在速度较大时增长迅速。

工程结构在设计寿命内遭遇地震概率最大，因此阻尼器在小震下应有良好耗能效果。考虑结构构件强度及承载能力，在罕遇地震下应限制阻尼器最大出力，因此建筑结构抗震设计中多采用α≤1的粘滞阻尼器。

结构未设置粘滞阻尼器时的动力平衡方程为：

(4)

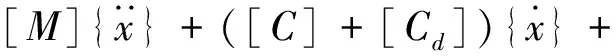
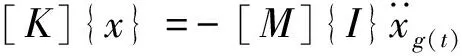
(5)

式中：[Cd]为阻尼器附加阻尼矩阵，由单元阻尼矩阵集成获得。比较式(4)、(5)可知，设置粘滞阻尼器可增加结构总阻尼，进而提高结构消能减震能力。

2 工程概况及计算模型

2.1 工程概况

某体育馆建筑位于西北高烈度地震带，抗震设防烈度为8°(0.2 g)，设计地震分组为第一组，场地类别为Ⅱ类。其钢结构屋盖造型为一双曲扁壳，扁壳中部隆起四周圆弧边逐渐降低，分别于四角交汇落地。屋盖采用纵横交错、主次分明、相贯焊接的空间桁架体系。整个屋盖横纵两方向跨度分别为150 m，120 m，顶部距地面高度24 m。屋盖结构边桁架在四个角处汇交，通过固定铰支座支撑于基础。中部用24个双向弹性铰支座与沿 ～ 轴及 ～ 轴，截面为600×600 mm混凝土柱连接以支承屋盖纵横向钢桁架传力。屋盖结构轴测图见图1，桁架构件均用Q345C的圆钢管，最大截面为Φ325×14。

图1 屋盖结构轴测图

2.2 计算模型

用通用有限元程序建立结构三维计算模型，主体结构各构件均用能考虑双非线性的铁木辛柯梁单元。双向弹性支座水平向及竖向弹簧系数分别取3 kN/mm，1280 kN/mm。粘滞阻尼器用基于Maxwell模型的弹簧阻尼单元，计算中不考虑粘滞阻尼器刚度，用线性阻尼参数[13]，整体结构有限元模型见图2。钢材选择考虑包辛格效应的经典双线性随动强化模型(BKIN)，混凝土本构关系采用多线性等向强化模型(MISO)[14]，材料参数见表1。时程分析用具有代表性[15]的El-Centro波及Kobe波进行三向输入，见图3。

表1 材料参数

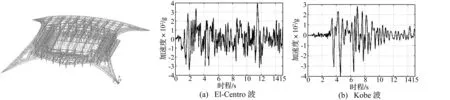
图2 有限元分析模型

3 阻尼器设置方案比选

图4 阻尼器设置示意图

对某体育馆屋盖增设粘滞阻尼器(图4)进行减震研究。为比较不同阻尼器布置方案的减震效果，进行常遇地震下弹性时程分析，地震波选加速度峰值70 cm/s2，持时15 s的El-Centro波沿结构三向输入(ax∶ay∶az=1∶0.85∶0.65)。由于地震作用屋盖水平方向响应较强，因此以减小屋盖结构水平向位移及加速度为减震控制目标，定义减震评价指标[16]为：

(6)

(7)

式中：ηu，ηa为屋盖节点位移及加速度减震率；ρu.max,βu.max为无控结构位移、加速度峰值绝对值；ργ.max,βγ.max为减震结构位移、加速度峰值绝对值。

3.1 阻尼器布设位置比较

该体育馆屋盖主桁架为倒三角截面，下弦面刚度较弱，由文献[17-18]并考虑施工可行性，在屋盖结构上弦面位移响应较大处布设40个阻尼系数为C=5 000 kN·s/m的线性粘滞阻尼器。所用五种减震控制方案见图5，图中红色构件为阻尼器单元，各减震方案阻尼器布设位置及特点见表2。

在El-Centro波激励下，五种减震方案的屋盖结构水平位移峰值、加速度峰值及减震率见表3、表4，峰值节点位置见图1。其中2073、2078、2085、2372号节点位于 轴侧短轴向边桁架中部下弦；2063、2067、2068号节点位于 轴侧长轴向边桁架中部下弦；1907号节点位于 轴与 轴相交处主桁架上弦。

表2 阻尼器布设位置及特点

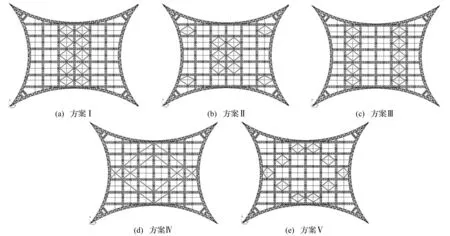
图5 五种阻尼器布设方案

表3 屋盖水平位移峰值及减震率(常遇地震)

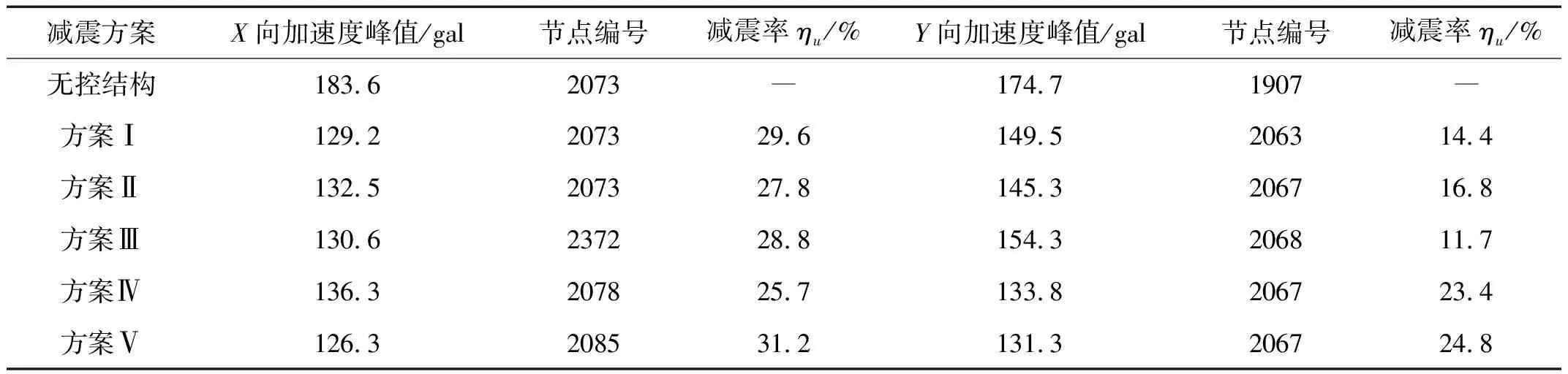
表4 屋盖水平加速度峰值及减震率(常遇地震)

对不同减震方案进行比较可见，方案ⅠX向位移及加速度减震效果较好，均达到了30%左右，但其Y向减震效果只有不到20%，原因是阻尼器在Y向集中设置，使屋盖该向振动速度受到抑制，粘滞阻尼器未充分发挥作用。方案Ⅱ、方案Ⅲ减震效果相似，优于方案Ⅰ且Y向减震效果有所提高，但仍低于X向。方案Ⅳ与前面三种方案相反，Y向位移减震效果优于X向。方案Ⅴ水平位移减震率约33%，X、Y向加速度减震率分别为31.2%及24.8%，各向减震效果均较好。

3.2 阻尼器阻尼系数比较

选减震效果最优方案Ⅴ，取C=1000、2000、3000、4000、5000、6000、7000、8000 kN·s/m的阻尼系数对粘滞阻尼器减震效果进行参数验证。

由图6看出，粘滞阻尼器减震效果与阻尼系数并非单调的线性关系，当C≤5000 kN·s/m时，提高阻尼系数减震率增长较快。而当C>5000 kN·s/m时，减震率增幅变缓，由于增加阻尼系数虽能增大阻尼力，但亦使粘滞流体粘度随之增大，阻尼器两端相对变形减小，限制了耗能能力的提高，故取阻尼系数C=5000 kN·s/m时减震效果较好。

图6 方案Ⅴ不同阻尼系数减震率比较

4 罕遇地震时减震分析

为研究粘滞阻尼器在罕遇地震时对结构减震控制效果，选用加速度峰值400 gal的El-Centro波及Kobe波，对方案Ⅴ进行三向激励弹塑性时程分析，阻尼器仍用C=5000 kN·s/m的线性粘滞阻尼系数。重点考察粘滞阻尼器对屋盖结构在罕遇地震时水平位移、加速度及构件内力减震控制情况。

4.1 水平位移、加速度减震控制

屋盖水平位移、加速度减震分析结果见表5、表6。El-Centro波激励下无控结构X、Y向峰值位移分别达112.8 mm、97.4 mm；Kobe波激励下达142.8 mm、105 mm。设置粘滞阻尼器后水平位移减震率达30%，水平加速度减震率在20%～40%间，不同频谱特性地震波作用下位移减震率差别不大，但加速度减震率差别较大。

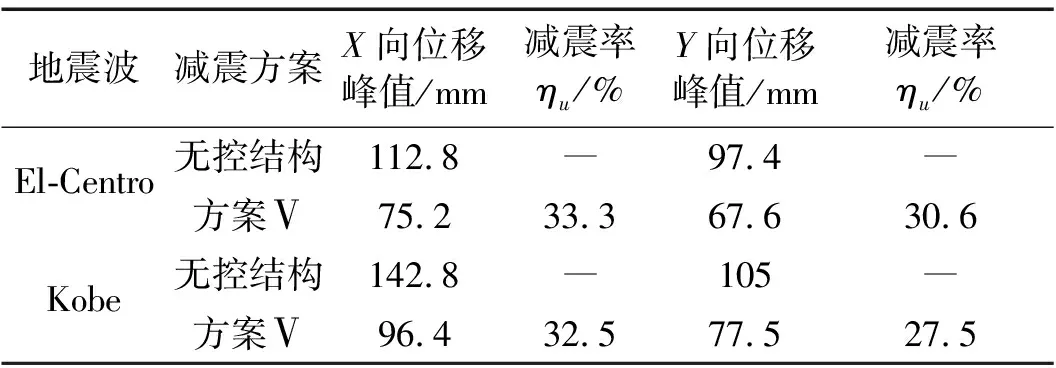
表5 屋盖水平向位移峰值及减震率(罕遇地震)

无控结构在El-Centro波输入下水平位移峰值出现在2073号节点X向和2068号节点Y向，Kobe波输入下水平位移峰值出现在2086号节点X向和2068号节点Y向。将不同地震波激励下，峰值节点的位移绘制成图7、图8时程曲线进行对比，可见减震方案Ⅴ在罕遇地震下能有效控制节点水平位移幅值。

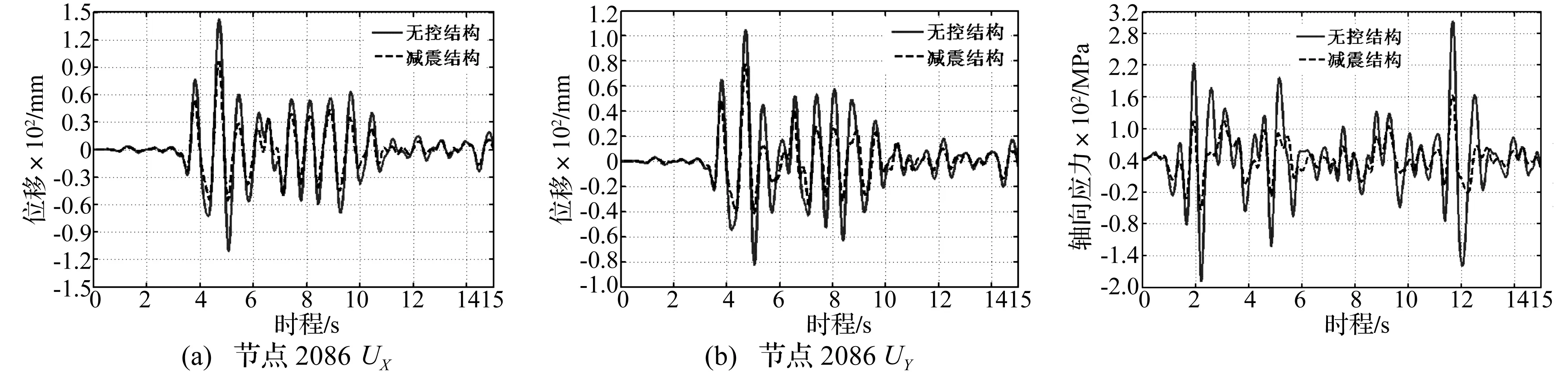
图8 峰值节点水平向位移时程曲线-Kobe

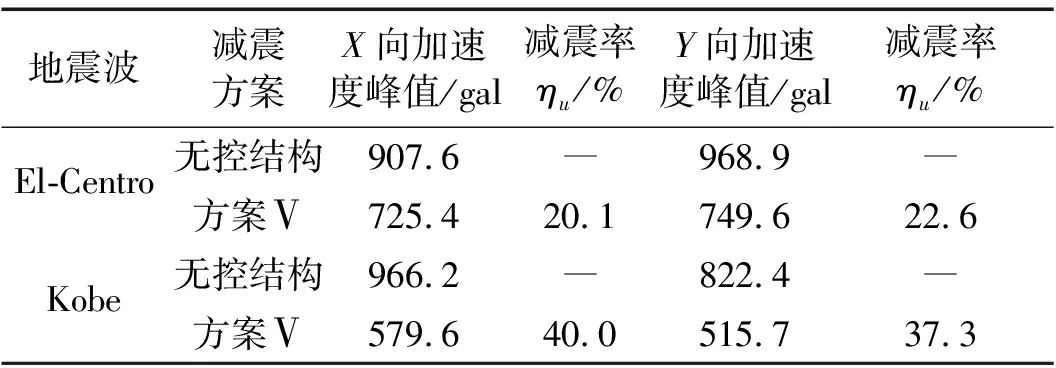
表6 屋盖水平向加速度峰值及减震率(罕遇地震)

4.2 构件内力减震控制

无控结构在El-Centro波激励下屋盖②轴与ⓒ轴主桁架相交处单元编号3328的上弦面腹杆进入塑性屈服。Kobe波激励下屋盖无构件进入塑性，但部分构件Mises等效应力接近材料屈服强度，应力最大值出现在④轴与轴主桁架相交处单元编号3681的上弦面弦杆。忽略桁架构件弯曲次内力，绘制3328号及3681号杆件轴向应力时程曲线见图9、图10。大震作用下3328号腹杆最大应力幅值由310 MPa减小到160 MPa，3681号弦杆最大应力幅值由291 MPa减小到157 MPa。图11为Kobe波激励最强时刻，屋盖局部区域Mises应力超过150 MPa的杆件分布。可见减震结构中高应力杆件数量明显减少。因此减震方案Ⅴ能有效控制构件内力幅值、降低地震作用时构件发生强度破坏或失稳破坏概率。

4.3 粘滞阻尼器耗能特征

比较大震减震方案Ⅴ各阻尼器单元的荷载-位移曲线看出，阻尼力幅值与变形幅值均相差不大，滞回曲线为典型速度相关型阻尼器耗能过程，且呈不规则椭圆形状。取⑥轴与轴间单元号11032的阻尼器，绘制在El-Centro波、Kobe波作用下荷载-位移曲线见图12，可见线性粘滞阻尼器变形幅值达5 mm，最大出力接近250 kN，滞回环饱满表现出良好的消能减震性能。

图12 11032号阻尼单元滞回曲线

不同地震烈度的时程分析表明，合理布置粘滞阻尼器的屋盖结构位移、加速度及构件内力幅值均明显减小。可用能量分布表达式概述其减震机理：

无控结构：

ET=ES+EC+Ep

(8)

减震结构：

ET=ES+EC+Ep+ED

(9)

式中：ET为地震输入总能量；ES为结构振动机械能；EC为结构阻尼耗散能量；EP为结构非弹性变形耗散能量；ED为粘滞阻尼器耗散能量。

由此，地震输入能量被减震结构引向专设的粘滞阻尼器吸收并耗散。强震发生时随结构变形的增大，粘滞阻尼器产生的阻尼亦增大，消耗大量输入结构的地震能量而保护主体结构安全，使空间结构达到 “小震经济、中震不坏、大震可修”的抗震设计目标。

5 结 论

通过用粘滞阻尼器对大跨空间桁架结构减震控制研究，分析体育馆屋盖在常遇及罕遇地震作用下动力响应规律，结论如下：

(1)常遇地震时在屋盖上均匀布置粘滞阻尼器，在水平两方向均能发挥较好减震作用。

(2)在减震方案Ⅴ基础上进行不同阻尼系数对减震效果的参数化验证表明，阻尼系数并非越大越好，需优化设计。本文所用5000 kN·s/m阻尼系数减震效果较好。

(3)罕遇地震时不同频谱特性地震波激励的屋盖位移减震率差别不大，而加速度减震率存在较大差别。

(4)减震结构能有效控制罕遇地震下构件内力幅值，结构各构件均处于应力较小的弹性状态，粘滞阻尼器对降低构件发生强度破坏或失稳的概率意义明显。

(5)粘滞阻尼器的荷载-位移曲线呈典型速度相关型耗能特征，且滞回曲线饱满，消能减震能力良好。

参 考 文 献

[1]董石麟，邢 栋，赵 阳.现代大跨空间结构在中国的应用与发展[J].空间结构,2012,18(1):3-16.

DONG Shi-lin, XING Dong, ZHAO Yang. Application and development of modern long-span space structures in China[J]. Spatial Structures, 2012, 18(1):3-16.

[2]叶继红，陈明月，沈士钊. TMD减震系统在网壳结构中的应用[J]. 哈尔滨建筑大学学报,2000,33(5):10-14.

YE Ji-hong, CHEN Ming-yue, SHEN Shi-zhao. The present situation of seismic vibration control of reticulated shell structures using TMD system[J]. Journal of Harbin University of C. E& Architecture, 2000,33(5):10-44.

[3]翁大根，张 超，彭林海，等. 附加黏滞阻尼器减震结构实用设计方法研究[J]. 振动与冲击,2012,31(21): 80-88.

WENG Da-gen, ZHANG Chao, PENG Lin-hai, et al. Practical design procedure for a energy-dissipated structure with viscous dampers[J]. Journal of Vibration and Shock, 2012, 31(21): 80-88.

[4]邓稳平,王 浩,李爱群,等. 高烈度区连续梁桥减震的粘滞阻尼器参数分析[J]. 振动与冲击,2012,31(16): 92-97.

DENG Wei-ping, WANG Hao, LI Ai-qun, et al. Parametric analysis of viscous dampers for earthquake mitigation of continuous bridges in high intensity region[J]. Journal of Vibration and Shock, 2012, 31(16): 92-97.

[5]Motohiko Y. Vibration control of large space structure using TMD system[A]. Proceedings of 15thAsian-Pacific Conference[C].on Structural Engineering and Construction,Cold Coast, Queensland, Australia, 1995:23-30.

[6]叶继红，陈明月，沈士钊. TMD系统在单层柱壳振动控制中的参数分析[J]. 工业建筑,2000,30(4):9-13.

YE Ji-hong, CHEN Ming-yue, SHEN Shi-zhao. Parametric analysis of TMD systems in vibration control of single layer latticed barrel vaults[J]. Industrial Construction, 2000, 30(4):9-13.

[7]范 峰，沈士钊. 单层柱面网壳的粘滞阻尼器减振分析[J]. 世界地震工程,2003,19(2):27-32.

FAN Feng, SHEN Shi-zhao. Vibration reduction analysis of viscous damper on single-layer reticulated vaults[J]. World Information on Earthquake Engineering, 2003, 19 (2):27-32.

[8]张毅刚，梁海彤. 替换可控杆件的双层柱面网壳半主动控制策略[J]. 北京工业大学学报,2003,29(3): 320- 324.

ZHANG Yi-gang, LIANG Hai-tong. Semi-active control srategy of double layer cylindrical lattice shell replacing controllable chords[J]. Journal of Beijing Polytechnic University, 2003, 29 (3):320-324.

[9]朱礼敏，钱基宏，张维嶽. 双层柱面网壳采用粘滞阻尼器的减震参数分析[J]. 建筑结构学报,2007,28(4): 58-63.

ZHU Li-min, QIAN Ji-hong, ZHANG Wei-yue. Parameter analysis o f vibration reduction of double-layer cylindrical latticed shell with viscous dampers[J]. Journal of Building Structures, 2007, 28 (4):58-63.

[10]Makris N, Constantinou M C. Viscous dampers: testing, modeling, application in vibration and seismic isolation[R]. Technical Report NCEER-90-0028, National Center for Earthquake Engineering Research, Buffalo, New York, 1990.

[11]Soong T T, Dargush G F. Passive energy dissipation systems in structural engineering[M]. England:Chichester, John Wiley & Sons Ltd.,1997.

[12]薛彦涛，李树利，李 博. 液体粘滞阻尼消能减震结构设计方法[J]. 建筑科学,2003,19(3):19-21.

XUE Yan-tao, LI Shu-li, LI Bo. Design of structures with fluid viscous dampers for earthquake energy dissipation[J]. Building Science, 2003, 19(3):19-21.

[13]朱礼敏. 大跨空间结构采用粘滞阻尼器的减震分析和优化设计[D]. 北京：中国建筑科学研究院，2007.

[14]刘 飞，汪大海，许 敏，等.某超限大跨度结构弹塑性地震反应分析[J]. 土木工程学报，2010，43(11)：27-35.

LIU Fei, WANG Da-hai, XU Min, et al. Analysis of the elastic-plastic seismic response of an ultra large span structure[J]. China Civil Engineering Journal, 2010, 43(11):27-35.

[15]曲 哲，叶列平，潘 鹏. 建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J].土木工程学报,2011,44(7):10-20.

QU Zhe, YE Lie-ping, PAN Peng. Comparative study on methods of selecting earthquake ground motions for nonlinear time history analyses of building structures[J]. China Civil Engineering Journal, 2011, 44(7):10-20.

[16]张微敬，钱稼茹，沈顺高，等. 北京A380机库采用粘滞阻尼器的减振控制分析[J]. 建筑结构学报，2009，30(2);1-7.

ZHANG Wei-jing, QIAN Jia-ru, SHEN Shun-gao, et al. Vibration reduction analyses of Beijing A380 hangar structure with viscous dampers [J]. Journal of Building Structures, 2009, 30(2):1-7.

[17]李正英,李正良,汪之松,等. 粘滞阻尼器拱桥结构减震控制研究[J]. 振动与冲击,2007,26(1):56-60.

LI Zheng-ying, LI Zheng-liang,WANG Zhi-song, et al. Study on seismic response control of an arch bridge with viscous dampers[J]. Journal of Vibration and Shock, 2007, 26(1):56-60.

[18]社团法人日本隔震结构协会．被动减震结构设计·施工手册[M]. 北京：中国建筑工业出版社,2008．