基于傅里叶幅值检验扩展法的轨道车辆垂向模型全局灵敏度分析
2014-09-05余衍然姚林泉朱忠奎
余衍然, 李 成, 姚林泉, 朱忠奎
(苏州大学 城市轨道交通学院,江苏 苏州 215006)
随我国列车运行速度的不断提高,轮轨间相互作用愈加显著、剧烈,轨道列车的动力学性能问题,如在高速运行下列车的稳定性、乘坐舒适性及运行安全性等越来越受到重视。提升列车的动力学性能,须对车辆系统模型参数进行优化设计。考虑轨道车辆涉及的建模工作愈加复杂,如“车辆-轨道-桥梁”耦合系统中,模型系统设计参数数目较庞大。因此,需对车辆模型系统进行参数灵敏度分析,以便确定调整设计参数对改变模型结构特性效果影响,去除对车辆动力学性能影响不大参数,为模型参数优化过程提供可靠的理论依据与工程参考。
参数灵敏度分析为评价因模型参数的不确定性引起模型结构特性变化程度方法。影响程度即灵敏度。按模型分析不同思路,灵敏度分析法可分为局部灵敏度分析法[1]与全局灵敏度分析法。前者为每次只改变某单一参数取值,对其余参数取其各自中心值,以此获得模型响应输出,评价考察单一参数发生变化时模型结果的变化量。该方法包括解析法(即直接求导法)、有限差分法及格林函数法等[2],适用于目标函数表达式简单、灵敏度微分方程较易推出、不确定性因素较少的系统模型。而全局灵敏度分析[3]考虑参数选取的实际概率分布,所有因素允许同时变化,变动范围可扩展到因素的整个定义域,故该方法不仅能反映局部情况,且可反映整个参数空间的变化对目标函数影响。全局灵敏度分析允许各参数在不同数量级取值变化,而局部灵敏度分析则不能保证在此情况下的有效性[4]。局部灵敏度分析要求目标函数有明确易推导的解析表达式;全局灵敏度分析目标函数只需有确定的输入、输出关系即可。此外,全局灵敏度分析亦考虑各输入参数间交互作用对目标函数影响;局部灵敏度分析则假定输入参数间相互独立且互不影响。因此,全局灵敏度分析较局部灵敏度分析更具优越性,且可分为定性、定量分析两类。定性全局灵敏度分析可以较小的计算量定性按灵敏度大小对各输入参数排序,包括多元回归法、Morris法、傅里叶幅度灵敏度检验法(Fourier Amplitude Sensitivity Test,FAST)等。定量全局灵敏度分析可定量确定各模型参数对模型结果误差的贡献率,目前有Sobol’与傅里叶幅值灵敏度检验扩展法(Extend Fourier Amplitude Sensitivity Test,EFAST)两种[3],且均基于方差方法,认为结果方差可完全反映模型结果的不确定性。鉴于此,全局灵敏度分析法在舰艇设备、生态模型、可靠性等多领域参数灵敏度分析中获得应用[3-5]。但轨道车辆模型参数的全局灵敏度分析研究目前尚未见报道。已有研究中,多利用局部灵敏度分析方法研究轨道车辆模型系统的振动特性,如张立民等[6]利用局部灵敏度分析法中直接求导法对车辆垂向悬挂参数进行灵敏度分析。结果表明,增加二系悬挂刚度可同时提高车体沉浮、点头及构架沉浮振动频率。吴会超等[7]建立高速车辆三维刚柔耦合动力学模型,分析车下设备质量偏心及弹性悬挂参数小范围变化对车体振动响应影响程度。
本文引入全局灵敏度分析法,将EFAST分析法直接应用于轨道车辆垂向模型中,以垂向模型系统绝对传递率为目标函数,计算模型相关参数灵敏度,讨论分析算例结果,为车辆系统模型参数灵敏度分析及优化设计提供更全面的参考依据。
1 傅里叶幅值灵敏度检验扩展法
EFAST法基本原理为选取合适的搜索曲线在由各参数组成的多维空间内搜索,将一组非线性相关整数频率分配给每个输入参数,并对模型系统每个输入参数搜索函数引入共同的独立变量,使模型成为独立变量的周期函数,从而使多维积分转化为一维积分。然后将目标函数展开为傅里叶级数,分别获得各频率的傅里叶频谱曲线,获得每个参数及参数间相互作用引起的模型结果方差在总模型结果方差中所占比例,此即为该参数灵敏度。因此,在分析过程中首先为每个需分析参数设定一搜索函数[1]:
xn=Gn[sin(ωns)]
(1)
式中:n为参数数目。序列{ωn}的选取需满足非线性相关,即:
(2)
其中:rn为整数;s为共同独立变量,在(-π,π)区间内等间隔取Ns个值,Ns=2Mωmax+1,其中M取4,ωmax为各参数对应频率组成的序列中最大值。
式(1)中Gn应满足[1]:
(3)
其中:Pn为xn的概率密度函数。将式(3)转化为[8]:
(4)
对式(4)等号两边积分,得在xn所属概率分布下搜索函数表达式。将搜索函数代入模型结果y=f(x1,x2,…,xn)便可转化为y=f(s),并由傅里叶展开得[3]:
(5)
其中:
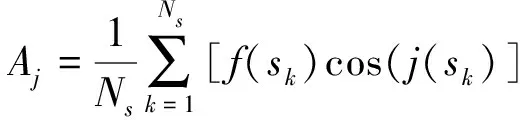
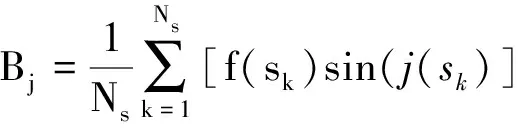

式中:sk=π/Ns(2k-Ns-1)为s在[-π,π]内的等间隔取样值。
(6)
其中:Z0=Z-{0}。则总方差为[1]:
(7)
将s在区间[-π,π]内等间隔取样所得每个参数输入模型,经多次计算,通过上述方程总可获得每个参数引起的方差Vn及模型结果总方差V。因此xn一阶灵敏度为:
(8)
计算xn总灵敏度可先给xn一较大频率ωn,给剩余参数设定一组较小的各不同频率{ωn’},且满足关系ωn≥2Mmax{ωn’}[9]。便将频谱分割成两部分[1,Mmax(ω’n)](含除xn外的其它参数频率)与[Mmax(ω’n+1),(Ns-1)/2](含xn在高频范围内影响)。
计算参数xn总灵敏度公式[9]为:
(9)
由以上分析知,EFAST第一阶灵敏度反映参数独立作用对模型输出影响,而参数总敏感度则反映参数间作用对模型输出影响。若所得总灵敏度数值与一阶灵敏度非常接近,说明参数间交互作用不明显。
2 车辆垂向模型参数全局灵敏度计算
2.1 垂向振动模型及目标函数设定
典型轨道车辆垂向模型见图1,其中Mc,Jc,Mt分别为车体质量、车体点头转动惯量、构架质量;Kpz,Cpz及Ksz,Csz分别为一二系悬挂刚度及阻尼;lc,lt分别为车辆定距之半与及转向架固定轴距之半;Zc,βc为车体垂向位移、点头角位移;Zt1(t2),Z01(02,03,04)分别为2个构架垂向位移及4副轮对处所受垂向输入激励;v为车辆行驶速度。
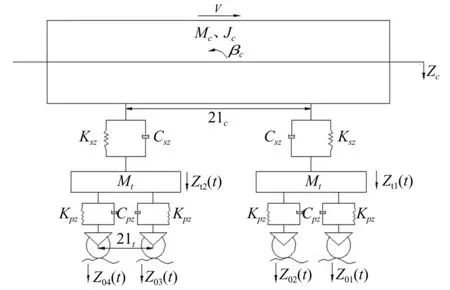
图1 轨道车辆垂向模型
据轨道车辆垂向物理模型,得运动微分方程组[10]:
(10)
由于构架点头运动与车辆垂向振动系统其它运动不耦合,不影响车体运动,故只考虑4个自由度,Z01(t),Z02(t),Z03(t),Z04(t)间关系为:
(11)
其中:τ1=2lt/v,τ2=2lc/v,τ3=2(lt+lc)/v为轮对时间滞后量,v为车辆行驶速度。
将式(10)用矩阵形式可表示为:
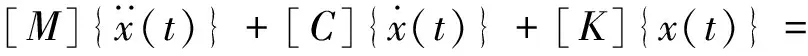
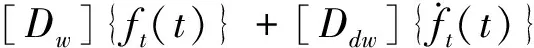
(12)
其中:[M],[C],[K]分别为系统质量、阻尼、刚度矩阵;[Dw],[Ddw]分别为激励位移、速度输入矩阵;{ft(t)}为系统位移激励输入项;{x(t)}为系统位移响应矢量。
对式(10)进行拉普拉斯变换得:
([M]s2+[C]s+[K]){x(s)}=
([Dw]+[Ddw]s){ft(s)}
(13)
移项并用虚宗量iω代替复宗量s,得系统频率特性为:
[H(iω)]=(-[M]ω2+i[C]ω+
[K])-1([Dw]+i[Ddw]ω)
(14)
综合以上各式,计算车体垂向振动绝对传递率T(ω)(即频率特性的模[11])幅频特性,见图2。各输入参数包含在系统质量、阻尼、刚度矩阵中,由式(14)知,参数取值发生变化,会致频率特性矩阵中对应元素大小变化,从而可建立输出与输入参数间联系。
图2分别给出车体垂向振动绝对传递率在悬挂参数优化区间的上下限值、中间值处曲线。其中图2(c)中三者几乎重合,说明一系悬挂刚度取值变化对绝对传递率影响甚微,该绝对传递率对参数变化不敏感。由图2看出,在优化区间内,轮对对车体垂向振动绝对传递率影响因素中,二系悬挂阻尼最显著,一系次之,而后为二系悬挂刚度,一系悬挂刚度影响甚微。而绝对传递率峰值大小对参数变化最敏感。因此,设定目标函数为绝对传递率T(ω)在1~20 Hz范围内最大值-max[T(ω)]较合理。绝对传递率越小,系统响应越小,其动力学性能也越好。
2.2 实例计算
设目标函数为某确定频率范围内车体构架绝对传递率峰值。以车辆垂向模型参数为输入参数,用EFAST法进行车辆垂向模型全局灵敏度分析。参考常用轨道车辆模型参数数据,确定车体质量为Mc=33.6 t,车体点头惯量Jc=2 040 t·m2,该参数值保持不变,即二者不进行灵敏度分析,其它参数见表1。
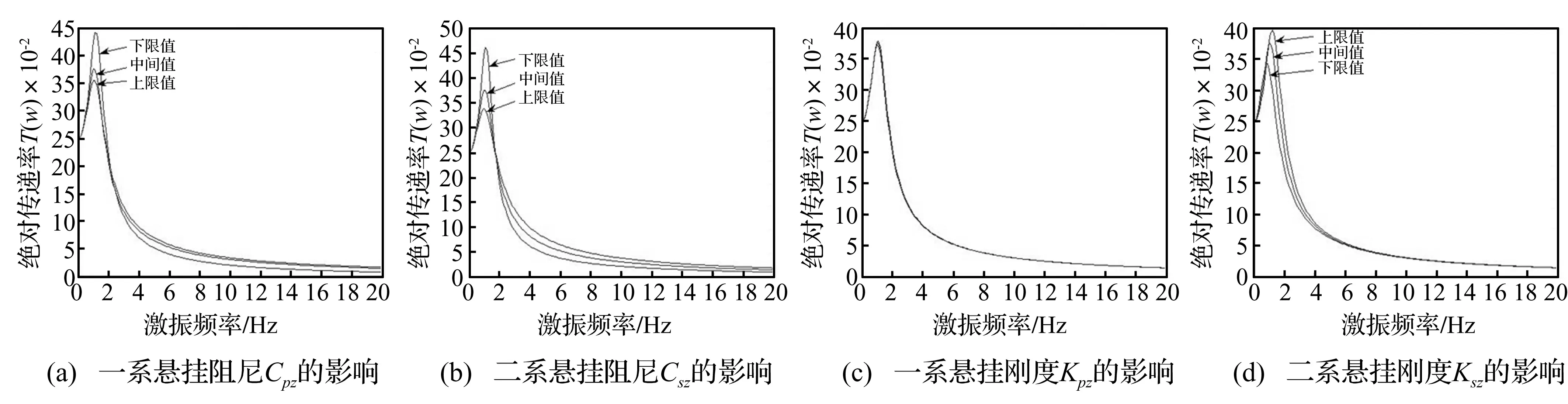
图2 车体垂向振动绝对传递率幅频特性

表1 车辆垂向模型参数概率分布
对均匀分布,文献[1]未能给出任意取值范围内的搜索函数,本文采用与文献[9]类似思路,即由式(1)推导出可在任意范围内取值的搜索函数,但区别在于本文推导中考虑随机相位Rn[1],使搜索函数搜索起点
可在优化区间内任意位置,使参数取值更均匀合理。搜索函数为:
(15)
其中:bn,an分别为参数取值上、下限,即参数优化范围;Rn为在(0,2π)上服从均匀分布的随机变量。据上述算法,用MATLAB编程,便可计算EFAST法全局灵敏度值。
2.3 结果分析
计算中,Mt为构架质量,Kpz为一系悬挂刚度,Cpz为一系悬挂阻尼,Ksz为二系悬挂刚度,Csz为二系悬挂阻尼,lc为车辆定距之半,lt为转向架固定轴距之半。车体垂向振动绝对传递率参数灵敏度计算结果见图3。由图3看出,一、二系悬挂阻尼、二系悬挂刚度位居前三,其它参数灵敏度值均较小。

图3 车体垂向振动绝对传递率参数灵敏度
灵敏度值代表因参数变化而引起目标函数的变化程度,即其它参数变化对绝对传递率峰值影响不大,但并非此参数对绝对传递率贡献不大。二系悬挂对绝对传递率影响较一系悬挂大,即二系悬挂刚度较一系悬挂刚度影响大,二系悬挂阻尼较一系悬挂阻尼影响大。分析结果与图2计算结果及文献[12]研究结论互相吻合,证明本文所用全局灵敏度分析法为行之有效的研究途径,EFAST法能正确反映车辆垂向模型参数对隔振效果影响。车体点头运动绝对传递率参数灵敏度计算结果见图4。对比图3、图4,车体点头运动绝对传递率变化程度同样受一系悬挂阻尼及二系悬挂参数影响较大,但车辆定距之半影响不可忽略。此可通过分析车辆垂向模型运动微分方程式(10)知,虽车辆定距之半对车体垂向位移无影响,但对车体点头运动则为重要参数。
分析轮对对其所属构架绝对传递率大小变化影响。由图5看出,最主要参数为一系悬挂阻尼,灵敏度值达0.9,二系悬挂刚度灵敏度值排第二,相对不大,其它参数基本可忽略。因两转向架相互独立,第二构架轮对对第一构架垂向振动作用通过车体浮沉运动及点头运动传递。故图6中二系悬挂参数与车辆定距之半灵敏度值相比较图5均明显提高。此外,图3~图6各自显示的总灵敏度较一阶灵敏度总体趋势相似,总灵敏度值有一定变化,但变化不很大,说明参数间存在彼此相互作用,影响不很大。若对车体及构架的沉浮运动与车体点头运动绝对传递率进行多目标优化,可综合考虑各部分参数灵敏度分析,筛选出参与优化过程参数。
3 结 论
采用EFAST法,本文首次对典型轨道车辆垂向模型隔振效果进行全局灵敏度分析。结论如下:
(1) 二系、一系悬挂阻尼及二系悬挂刚度取值变化对车体垂向振动绝对传递率影响较大;车体点头运动绝对传递率变化程度受一系悬挂阻尼、二系悬挂参数及车辆定距之半影响明显;轮对对其所属构架绝对传递率影响,主要为一系悬挂阻尼贡献;由于二者间作用力可通过车体相互传递,某转向架一、二系悬挂参数及车辆定距之半,对另一构架垂向振动亦存在一定影响;对比各参数总灵敏度与一阶灵敏度发现,各参数间存在一定相互作用,彼此并非完全独立,但相互影响较小。
(2) 本文研究能较好体现全局灵敏度分析EFAST法计算量较小、所得结果直观清晰、便于分析等优点,研究结果与采用其它方法结论一致,证明EFAST法可用于轨道车辆模型系统参数优化设计;其分析思路与研究方法也可适应更复杂的大型系统研究模型,如车辆空间模型、车辆-轨道-桥梁耦合系统等非线性问题。
参 考 文 献
[1]Saltelli A, Tarantola S, Chan K. A quantitative model-independent method for global sensitivity analysis of model output[J].Technometrics,1999,41(1):39-56.
[2]聂祚兴.车身噪声传递函数的全局灵敏度分析及稳健优化设计[D].长沙:湖南大学,2012.
[3]徐崇刚,胡远满,常 禹,等.生态模型的灵敏度分析[J].应用生态学报,2004,15(6):1056-1062.
XU Chong-gang, HU Yuan-man, CHANG Yu, et al. Sensitivity analysis in ecological modeling[J].Chinese Journal of Applied Ecology,2004,15(6):1056-1062.
[4]毛为民,朱石坚,陈 刚,等.隔振系统的灵敏度分析[J].海军工程大学学报,2007,19(2):68-71.
MAO Wei-min, ZHU Shi-jian, CHEN Gang,et al. Sensitivity analysis of vibration isolation system[J].Journal of Naval University of Engineering, 2007,19(2):68-71.
[5]汪宏伟,汪 玉,赵建华.EFAST法在管路系统冲击响应中的应用研究[J].振动与冲击,2010,29(4):197-199.
WANG Hong-wei, WANG Yu,ZHAO Jian-hua. Application of extended Fourier amplitude sensitivity test method in shock response of a piping system[J].Journal of Vibration and Shock, 2010,29(4):197-199.
[6]张立民,董铁军.铁道车辆悬挂系统振动特征频率灵敏度分析[J].振动与冲击,2009,28(1):28-31.
ZHANG Li-min,DONG Tie-jun. Analysis of eigen value sensitivity for a railway vehicle suspension system[J]. Journal of Vibration and Shock, 2009,28(1):28-31.
[7]吴会超,邬平波,吴 娜,等.车下设备悬挂参数与车体结构之间匹配关系研究[J].振动与冲击,2013,32(3):124-128.
WU Hui-chao,WU Ping-bo, WU Na,et al. Matching relations between equipment suspension parameters and a carbody structure[J].Journal of Vibration and Shock, 2013,32(3):124-128.
[8]Lu Y C, Mohanty S. Sensitivity analysis of a complex proposed geologic waste disposal system using the Fourier amplitude sensitivity test method[J].Reliability Engineering and System Safety,2001,72(3):275-291.
[9]Lauret P, Fock E,Mara T A. A node pruning algorithm based on a Fourier amplitude sensitivity test method[J]. Neural Networks, IEEE Transactions on,2006,17(2):273-293.
[10]曾 京,邬平波,郝建华.铁道客车系统的垂向减振分析[J].中国铁道科学,2006,27(3):62-67.
ZENG Jing, WU Ping-bo, HAO Jian-hua. Analysis of vertical reduction for railway vehicle systems[J].China Railway Science, 2006,27(3):62-67.
[11]丁文镜.减振理论[M].北京:清华大学出版社,1988.
[12]郝建华,曾 京,邬平波.铁路车辆垂向减振与悬挂系统参数优化[J].交通运输工程学报,2005,5(4):10-14.
HAO Jian-hua,ZENG Jing,WU Ping-bo. Vertical vibration isolation and suspension parameter optimization of railway vehicle[J]. Journal of Traffic and Transportation, 2005, 5(4): 10-14.
