基于λ-截集的均值-方差组合投资决策模型及其应用研究

付云鹏 ,马树才

(辽宁大学 a.信息学院；b.经济学院，辽宁 沈阳 110036)

基于λ-截集的均值-方差组合投资决策模型及其应用研究

付云鹏a,马树才b

(辽宁大学 a.信息学院；b.经济学院，辽宁 沈阳 110036)

以模糊数的截集为切入点给出一种模糊数可能性均值、可能性方差和可能性协方差的新的定义，并将新定义下的可能性均值作为证券组合投资未来收益率的度量，新定义下的可能性方差作为证券组合投资未来风险的度量，构建基于λ-截集的可能性均值-方差组合投资理论模型。并结合中国证券市场中的具体实例，说明了该模型的合理性和适用性。

三角模糊数;截集;可能性均值;可能性方差

0 引言及文献综述

组合投资理论研究投资者如何在不确定的收益和风险下选择优化组合投资，其核心问题是如何在风险环境下对资源进行合理的分配和利用。在此过程中，投资者一方面希望获得最大的期望收益，一方面希望承担最小的风险。组合投资决策问题的研究对象是一个极其复杂的系统，该系统影响因素多、结构复杂、信息变化快，投资决策者要在这样一个系统中分析资产的未来收益和风险，选择使其收益最大而所需承担风险最小的投资决策，因此对投资市场进行合理的描述是减少不确定投资因素的关键所在，也是困难所在。组合投资决策中的不确定性主要包括模糊性和随机性两个方面，对于随机性的处理大部分学者将投资的未来收益看成是随机变量，以概率论为基础处理信息的随机性；对于模糊性不同的学者采用不同的处理方式，研究了带有模糊信息的证券组合投资问题。早期的成果集中于用可能性变量来描述和度量风险资产的收益率和风险。Tanaka[1]等利用可能性变量来描述证券的收益率，利用证券历史收益率和未来市场之间的相似程度来确定证券未来收益率的分布函数，构建证券组合投资的中心差值模型。姚天祥和刘思峰[2]利用梯形模糊数来预测证券的未来收益率，并用其代替收益率的均值来作为未来收益的度量，提出了新的风险度量函数，构建新的组合投资模型。费忠华等[3]利用区间模糊数表示证券组合投资的期望收益率和风险损失率，通过构建区间数模糊线性规划模型，并利用区间数的排序算法对模型进行求解。也有学者从模糊决策的角度利用模糊约束条件和模糊目标函数来构建模型。M. Arenas Parra等[4]同时考虑了收益、风险和资金三方面的模糊因素，利用模糊约束条件和模糊目标函数来解决信息的模糊性问题。韩苗等[5]利用模糊决策理论对模糊环境下基于信息熵的组合投资模型进行求解，并通过实证分析检验了模型的适用性。邓雪和李荣钧[6]在Markowitz的均值-方差模型的理论框架下，通过构建模糊约束条件利用模糊遗传算法来求解模型，并利用实证分析说明了该算法的有效性和可行性。还有文献以模糊数的排序关系为依据构建新的基于模糊理论的组合投资决策模型。付云鹏等[7]通过定义随机变量为模糊数时的均值和方差构建基于模糊空间距离的投资组合模型，利用模糊数的排序准则对模型进行求解。孟凡永等[8]利用积分的思想给出了一种基于α-截集的模糊数序关系准则，本文借助孟凡永等的基于α-截集的模糊数的排序思想，利用直线y=λ与区间数上方隶属函数围成的面积和x轴与隶属函数围成的面积之间的比值作为权重，提出基于λ-截集的可能性均值和可能性方差的定义，并以此为依据构建基于λ-截集的均值-方差组合投资决策模型，并结合具体实例给出模型的实际应用，以检验该模型的适用性和有效性。

1 基于λ-截集的均值、方差

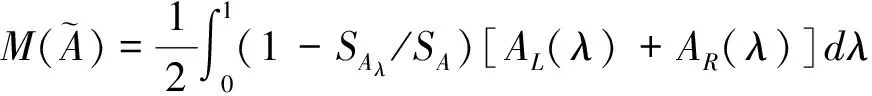
注：在此种定义方式中，用1-SAλ/SA作为相应的每个区间中点的权重，其区间端点的隶属函数的值越大权重就越大。

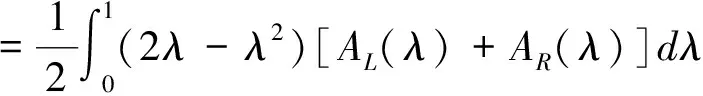
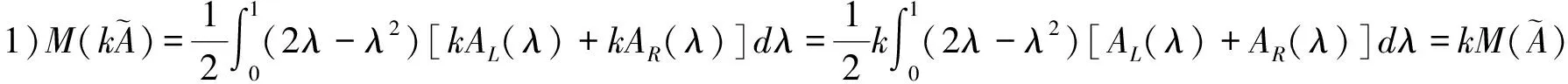
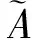
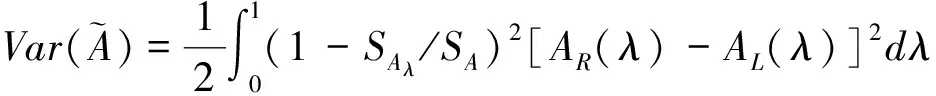
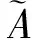
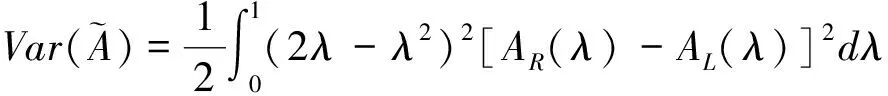
2 基于λ-截集的组合投资决策模型

2.1 模型构建

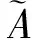
(1)

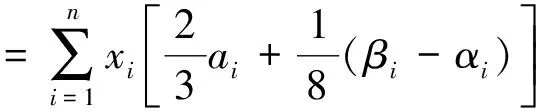
组合投资预期收益率的基于λ-截集方差为

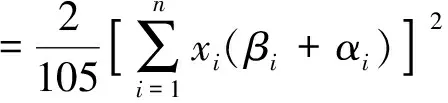
如果事先给定收益率的下限为μ(μ>0)，选择资产组合使该组合的总体风险最小的模型可表示如下：

(2)

模型(1)的等价形式为

(3)

模型(3)是普通的线性规划问题，可用单纯形法求其最优解，也可直接应用Lindo、Lingo和Matlab等求解规划问题的软件直接求解。

2.2 模型的应用

现选取我国证券市场中已上市的六种证券作为考察对象，证券代码分别为SH600104，SH600338，SH600000，SH600356，SH600085和SH600060，样本数据选取这六种证券从2009年1月到2010年2月近400个交易日的日收益率的均值作为每种证券的预期收益率。利用公式(1)求得上述六种证券的预期收益率数据，如表1所示。

表1 六种证券的期望收益率

注：数据来源于新浪财经，经整理并按公式(1)求出。

将表1中的数据带入模型(3)，用Lingo软件求解，可得不同收益率下的不同组合的投资结果，如表2所示。

表2 不同收益下限的投资组合

从表2中可以看出，对于不同的收益率水平，投资者所需承担的风险值是不同的，随着收益率的增加，投资者所需承担的风险增加，投资者可以根据自己的风险偏好来选择不同的投资组合。例如当某个投资者选择收益率的下限为0.005时，可选择证券SH600356和证券SH600060进行投资，投资比例分别为76.59%和23.41%，此时风险值为0.005 673 184。

3 结论

组合投资的核心问题就是研究投资者如何将资产在不同的风险资产进行合理的配置，以获取最大的收益，同时承担最小的风险。本文从模糊数的截集出发定义了模糊数的基于λ-的均值、方差和协方差，研究了这种定义下的均值、方差和协方差的性质，并以此为基础构建了基于λ-截集的组合投资决策模型，并将模型转化为普通线性规划问题进行求解；对于线性规划问题可以直接用Lindo、Lingo和Matlab等软件进行求解，使求解过程大大简化；最后结合我国证券市场中已上市的六种证券进行实证分析，结果表明该模型具有一定的实际应用价值。

[1] H Tanaka,P Guo,I B Turksen.Portfolio selection based on fuzzy probabilities and possibility distributions[J].Fuzzy Sets and Systems,2000,111(3):115-126.

[2] 姚天祥,刘思峰.基于预测收益率的模糊投资组合优化模型[J].统计与决策,2007(19):47-48.

[3] 费忠华,陈又星,姜忠义,等.区间值模糊线性规划在证券组合投资优化中的应用[J].数学的实践与认识,2010,40(7):25-30.

[4] M Arenas Parra,A Bilbao Terol,M V Rodríguez Uría.A fuzzy goal programming approach to portfolio selection[J].European Journal of Operational Research,2001(133):287-297.

[5] 韩苗,周圣武,仓定帮.基于熵的投资组合模糊优化模型[J].运筹与管理,2005,14(6):126-129.

[6] 邓雪,李荣钧.基于模糊遗传算法的自融资有效投资组合研究[J].经济数学,2009,26(4):91-96.

[7] 付云鹏,马树才,宋琪.基于模糊空间距离的组合投资模型及应用研究[J].数量经济技术经济研究,2012,9(8)：124-136.

[8] 孟凡永,曾雪兰,王飞,等.基于α-截集的模糊数排序方法研究[J].海南大学学报:自然科学版,2008,26(1):21-25.

2014-07-05

国家社科基金青年项目：基于空间计量分析的人口规模、结构对资源环境的影响效应研究(13CRK027)；辽宁大学亚洲研究中心项目：东北亚区域经济合作对中国产业结构优化与升级的影响效应研究(201209)

付云鹏(1978-)，女(满族)，辽宁铁岭人，辽宁大学副教授，经济学博士。研究方向：模糊数学、组合投资理论与计量经济模型； 马树才(1945-)，男，辽宁岫岩人，辽宁大学教授，博士生导师。研究方向：计量经济模型及方法。

F830.59

A

1008-4657(2014)04-0079-05

寸晓非]