双曲空间中的拉普拉斯算子
2014-09-04王全胜
王全胜
(荆楚理工学院 数理学院,湖北 荆门 448000)
双曲空间中的拉普拉斯算子
王全胜
(荆楚理工学院 数理学院,湖北 荆门 448000)
拉普拉斯算子是黎曼流形上一类重要的微分算子,流形上很多问题的研究都与拉普拉斯算子有关。文章得到了不同双曲空间模型中拉普拉斯算子的计算公式,利用这些计算公式,通过计算具体函数的拉普拉斯,可以直观地看到拉普拉斯算子与度量密切是相关的。
拉普拉斯算子;双曲空间;黎曼度量
0 引言
拉普拉斯算子是黎曼流形上一类重要的微分算子,流形上很多问题的研究都与拉普拉斯算子有关(如流形的谱问题),因而掌握拉普拉斯算子的计算方法是重要的。设M是一个n维的黎曼流形,g,△分别是M上的黎曼度量(度量也可用ds2表示)和拉普拉斯算子,当M的截曲率是常数时,这样的黎曼流形被称为空间形式。常见的空间形式有三种,而双曲空间形式(一般称为双曲空间)是其中一种,其截曲率为-1。空间形式是黎曼流形中很重要的模型,是学习黎曼流形的基础。而相对于另外两种空间形式欧氏空间和单位球来说,对双曲空间的理解就要困难一些。而在本文中,我们的目的就是要得到双曲空间中拉普拉斯算子的具体表述形式。但黎曼流形的度量并不是唯一的,而拉普拉斯算子与度量又密切相关,要完全给出双曲空间上拉普拉斯算子的表述形式非常困难。因此,在本文中,我们将先给出双曲空间的一些常见度量,然后给出这些度量下拉普拉斯算子的表述形式。下文先介绍一些与本文研究问题相关的知识。
1 预备知识
对于黎曼流形上的拉普拉斯算子,通常的定义的方法是先梯度后散度,即是由梯度算子和散度算子的一种复合算子。以下简要介绍这几种算子,具体细节可参看文献[1-2]。
(1)
设n维双曲空间Hn是n+1维欧氏空间Rn+1的浸入子流形,在文献[3]中,给出下述基本型:
H={(1,x2,…,xn+1):xn+1>0}
关于这三种基本型的度量分别为:
(2)
(3)
(4)
接下来,我们将给出在这三种度量下双曲空间的拉普拉斯算子的表述形式。
2 主要结果及其证明
在文献[4]中,作者给出了一类乘积流形上的拉普拉斯算子的具体表达式。在本节中,我们将导出在第1节给出的三种度量下双曲空间的拉普拉斯算子的表述形式。关于双曲空间的具体内容可参看文献[5]。
定理1 设双曲空间中,三种度量对应的拉普拉斯算子分别为ΔH,ΔI,ΔJ,则其分别为:

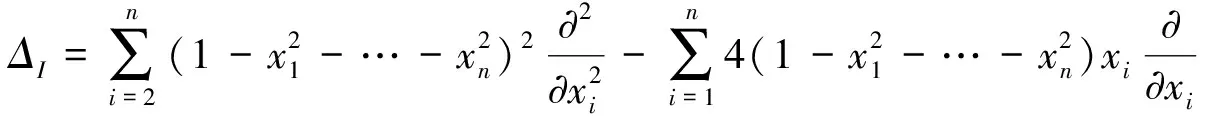

证明由式(2)可知,在第一种度量下,有:
再由式(1),可知
同样由式(2)可知,在第二种度量下,有:
同样由式(1),可知
作与前两种情形类似的计算,可知在第三种度量下,有:
gij=δij,i,j=1,…,n;gn+1,n+1=-1
再由式(1),可知
至此,定理1得证。
3 计算实例
下文给出一个拉普拉斯的计算实例。利用上文给出的拉普拉斯算子的计算公式,计算最后一个坐标函数xn+1的拉普拉斯算子。
例1 由定理1直接计算可得:
ΔHxn+1=(2-n)xn+1,
ΔKxn+1=0。
由上面的例子可以看到,拉普拉斯算子的计算和度量是密切相关的。
[1] 陈维桓,李兴校.黎曼流形[M].北京:北京大学出版社,2002.
[2] Petersen P.Riemannian geometry[M].2nd ed.New York:Springer,2006.
[3] Cannon J W.Hyperbolic geometry[J].Flavors of Geometry,1997(31):59-111.
[4] 王全胜.乘积流形R×N上的拉普拉斯算子[J].科技创新导报,2013(27):208.
[5] Anderson J W.Hyperbolic geometry[M].2nd ed.London:Springer,2006.
2014-04-02
王全胜(1973-),男,湖北公安人,荆楚理工学院讲师,硕士。研究方向:函数分析与几何分析。
O189.3
A
1008-4657(2014)04-0076-03
寸晓非]
