一种机载设备安装支架的动力特性优化
2014-09-04田玉艳
段 明,田玉艳
(中航工业试飞中心 改装部,陕西 西安 710089)
0 引言
1965年Niordson关于振动梁结构优化文献的问世,开创了结构动力优化的先河。在此之后的几十年中,结构动力优化越来越引起了人们的关注,已涉及到结构动力优化设计的理论、方法、建模、敏度分析、软件设计和工程应用等诸多方面。结构动力特性优化是结构动力优化研究的一个重要分支,它包括结构的固有频率、振型、刚度和质量分布等诸多方面,其中,以结构固有频率为目标或约束的优化是其中研究最早和成果相对较多的一个方面。目前,结构频率优化的对象主要为桁架、梁、刚架和薄板等单一类型的结构。
机载设备安装支架不同于一般地面设备支架,设计过程中一方面要使支架的固有频率远离机体结构的固有频率,避免共振破坏;同时,一些灵敏的机载电子设备,如雷达天线、采集器、记录器、惯导设备、振动传感器等对支架的动力特性尤其是低阶固有频率有着特殊的要求,一般表现为要求支架一阶固有频率大于某一特定值,才能保证设备可靠工作。因此,可以说机载设备安装支架动力特性的优劣关乎机体的结构安全和设备工作的可靠性。
在保证结构强度和刚度的条件下,减轻结构自重,增加有效载荷对飞行器有着极其重要的意义。本文对一种壁板结构机载设备安装支架进行了动力特性优化。
1 结构无阻尼自由振动方程及其求解方法
1.1 结构无阻尼自由振动方程
典型的多自由度系统的无阻尼自由振动方程为:

其中:M,K,X分别为结构的质量矩阵、刚度矩阵以及位移向量。
令X=Aeωt,则式(1)可以转化为矩阵M 和K 的广义特征值问题:

其中:ω为结构的固有频率;特征向量A表示结构的主振型。
因为A≠0,由式(2)可得:
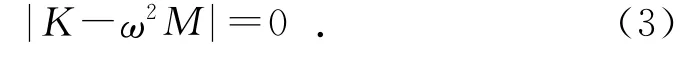
1.2 MSC.Nastran特征值求解方法
对于特征值和特征向量的求解,MSC.Nastran提供了3种算法:跟踪法(Tracking method)、变换法(Transformation method)以 及 兰 索 士 法 (lanczons method)。跟踪法的实质是迭代法,变换法是通过矩阵变换的方法求解特征值,兰索士法是一种将跟踪法和变换法结合起来的新的特征值解法。其中,跟踪法又分为逆幂法(INV)和移位逆幂法(SINV);变换法又分为HOU法、GIV法以及修正的HOU法(MHOU)、修正的GIV法(MGIV)。
3种求解方法的使用范围、求解特性、求解选项和计算量级的比较如表1所示。其中,N为刚度矩阵的维数,B为半带宽,E为特征值个数。
由于兰索士法的求解范围大、不会存在丢根现象等优点,同时考虑支架计算量不大以及只计算结构低阶固有频率等工程实际特点,在优化设计中本文选择兰索士法求解固有频率,这也是MSC.Nastran推荐和默认的求解方法。
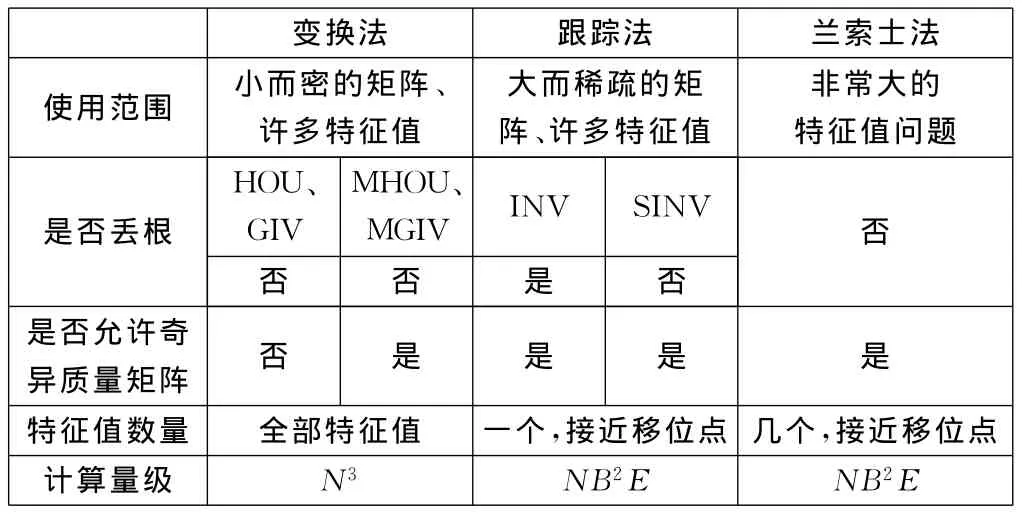
表1 特征值求解方法比较
2 优化模型
2.1 结构简介
设计如图1所示的加筋壁板结构形式的机载设备安装支架,在壁板周缘和内部布置“井”字形加强筋,以提高壁板刚度。在壁板左前位置开设方形孔,用以机载设备的地面维护。支架采用7070-T7451预拉伸硬铝合金板材机加工成形,通过周边的8个M6螺栓与机体连接。
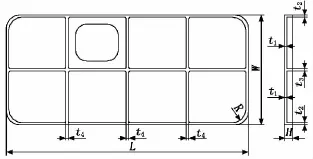
图1 机载设备安装支架结构简图
2.2 设计变量
加筋壁板结构的设计参数主要有壁板长度L、宽度W、高度H、筋条的数量及布置形式、底板壁厚t1、周边缘条壁厚t2、内部纵向筋条壁厚t3和横向筋条壁厚t4等。
由于机体结构接口尺寸的限制及机载设备布局要求,壁板的L、W、H、R通常是确定的参数即为常量,同时,设计方案已经确定了筋条的数量和布置形式,本文不涉及结构的形状或拓扑优化,因此选择t1,t2,t3和t4作为设计变量。
2.3 目标函数和约束条件
建立的优化数学模型是在满足结构一阶固有频率的约束条件下,使结构重量极小化。考虑机体结构和机载设备对支架固有频率的要求,约束条件设计为支架的一阶固有频率在145Hz~150Hz之间,同时考虑机械加工的工艺性,对设计变量的下限作了约束,即最小设计壁厚均取为1.5mm。优化数学模型可简记为:
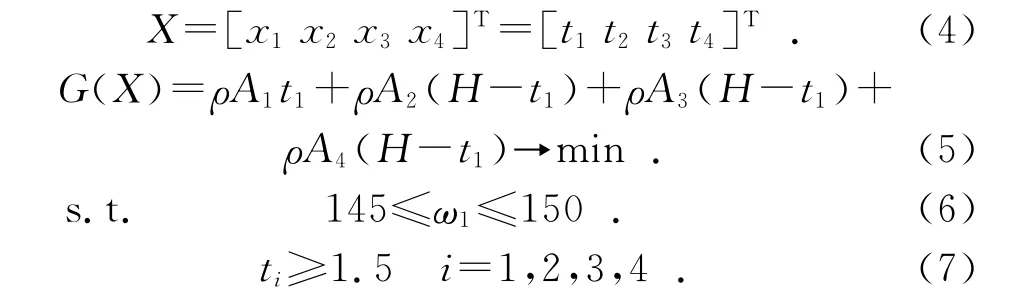
其中:G(X)为支架结构自重函数;A1,A2,A3,A4分别表示支架底板面积、周边缘条截面积、纵向筋条截面积、横向筋条截面积;ρ为材料密度;ω1为支架的一阶固有频率。
3 基于MSC.Patran/Nastran的动力特性优化计算
3.1 计算流程和有限元模型
基于MSC.Patran/Nastran进行动力特性优化计算,在求解前首先在Patran中创建结构的有限元模型,并定义结构的材料、单元属性和边界条件等;然后,定义结构的特征参数作为设计变量并赋初值,定义设计变量的区间范围,定义优化分析的目标函数、约束条件和迭代次数等;最后,设置求解参数和分析类型,调用Nastran动力优化模块SOL 200进行求解,并提取计算结果文件在Patran中进行后处理。动力特性优化分析典型的有限元求解流程如图2所示。

图2 动力特性优化的有限元求解流程图
在MSC.Patran中建立的加筋壁板结构支架的有限元模型如图3所示。模型共包含1 620个节点、1 482个四节点四边形壳单元。边界约束条件是对8处与机体连接的节点作固结约束。
3.2 计算结果
计算采用 MSC In House Optimizer,优化算法选择为 Mod.Method Feasible Dir.(MMFD),设计变量初值均赋为4,最大迭代设计次数设置为30。设计变量经过各次迭代的取值如表2所示,图4为设计变量变化曲线,目标函数即支架结构自重变化曲线如图5所示。
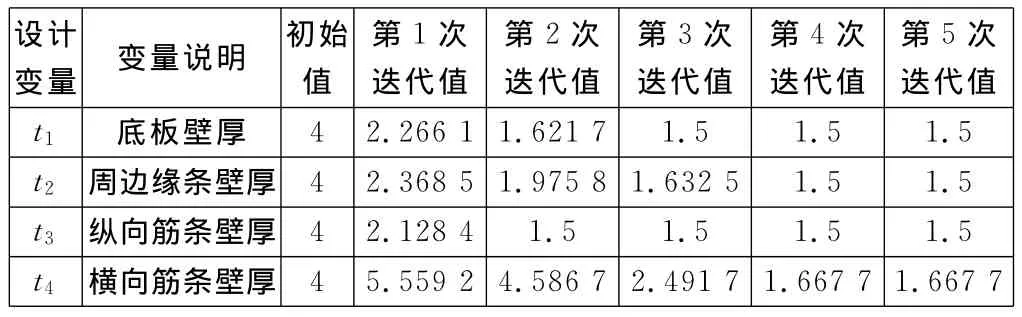
表2 设计变量变化值
3.3 计算结果的校核
以设计变量经过5次迭代后的最优值作为分析参数,结构的材料特性、单元特性、边界条件及网格划分不变,校核结构的固有频率。计算结果表明:优化后结构的一阶固有频率为145.59Hz,在频率约束区间范围内,并接近区间下限。
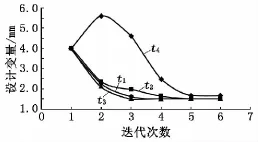
图4 设计变量变化曲线
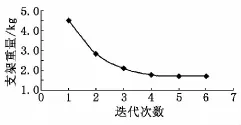
图5 目标函数变化曲线
4 结论
(1)在结构形式确定的情况下,对一种壁板结构机载设备安装支架的动力特性进行了优化设计,快速而准确地确定了支架的底板壁厚、周边筋条壁厚及内部筋条壁厚等结构设计参数,不但使结构低阶固有频率满足要求,而且此时结构自重最轻,为结构设计提供了理论依据,较好地解决了工程实际问题。
(2)以设计变量经过迭代后的最优值作为分析参数,校核结构的一阶固有频率,确认了优化结果的可信性,本文可作为同类结构优化设计的参考。
[1] 陈建军,车建文,崔明涛.结构动力优化设计述评与展望[J].力学进展,2001,31(2):181-192.
[2] 钱令希.工程结构优化设计[M].北京:水利电力出版社,1983.
[3] 田利思,李相辉,马越峰,等.MSC Nastran动力分析指南[M].北京:中国水利水电出版社,2012.
[4] 薛运虎.基于演化算法的结构动力优化设计研究[D].北京:北京邮电大学,2011:3-7.
