四元数矩阵的特征值与特征多项式*
2014-09-04黄莉
黄 莉
(武汉商学院信息工程系 湖北武汉 430056)
四元数矩阵的特征值与特征多项式*
黄 莉
(武汉商学院信息工程系 湖北武汉 430056)
本文研究了四元数矩阵的右特征值、左特征值的存在性,并且比较了它们之间的差异,最后给出了在特殊情况下四元数矩阵右、左特征值统一的一个充分条件.
四元数矩阵,复表示阵,特征值,特征多项式
由于四元数乘法不满足交换律,这使得四元数矩阵的特征值与特征多项式的定义及性质比常规矩阵复杂得多.
设R为实数域,C为复数域,记
Q{q|q∈R+Ri+Rj+Rk,ij=-ji=k,i2=j2=k2=-1}

定义1[1]设A∈Qn×n,若存在λ∈Q及0≠α∈Qn×1,使得Aα=αλ(或Aα=λα),则称λ为A的右(或左)特征值.而称α为A的属于右(或左)特征值λ的特征向量,如果λ既是A的右特征值,又是A的左特征值,则称 为A的特征值.
注:①四元数矩阵A的右特征值不一定是左特征值,反之,左特征值也不一定是右特征值.
②由Aα=αλ⟹A(αq)=(Aα)q=αλq=αqq-1λq(∀q∈Q)知若λ为A的右特征值,则任何与λ在Q上相似的四元数q-1λq也为A的右特征值,故A的右特征值若存在则有无穷多个,记这无穷多个右特征值的集合为[λ].但左特征值没有这样的性质.
定义2[2]设A∈Qm×n,则称‖λI-A‖为A的重特征多项式,记为FA(λ),即FA(λ=‖λIn-A‖.
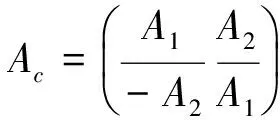
引理1[1]设A=A1+A2j∈Qm×n,其中A1,A2∈Cm×n则AH=A1H-A1Tj.
引理2[3]设A,B∈Qn×n,则Ac=Bc⟺A=B;(A+B)c,(AB)c=AcBc;(f(A))c=f(Ac)其中f(x)为R上多项式.
定理1[4]一个复数λ是四元数矩阵A∈Qn×n的一个右特征值⟺λ为A的拟特征多项式fAc(λ)的根.
以常见的居住建设项目选址为例,由于居住用地项目主要以多层、中高层及高层单元式居住建筑为主、配套设施齐全、布局完整的用地,该类项目在城市分布广泛,在居住用地中占主导地位。因此,在选址过程中,除了考虑政府的管控限制条件,还需权衡区位交通便捷度、市政交通的可达性、公共服务设施配套。根据设定的因子评价体系对筛选出来的符合条件候选图斑进行综合打分,最后生成选址分析对比报告如图6。
定理2[5]任何n阶四元数矩阵A至少有一个在Q上的左特征值.
证明(笔者用拓扑知识来反证)记Ax=λx为(λI-A)x=0,假设λI-A对于 非奇异,即(λI-A)x=0只有零解,也即A无左特征值,笔者下面考虑Q上的n阶可逆阵组成的线性群GL(n,Q),
令f(t,λ)∶=ft(λ)=tλI-A0≤t≤1, |λ|=1,
g(t,λ)∶=gt(λ)=λI-tA0≤t≤1 |λ|=1,
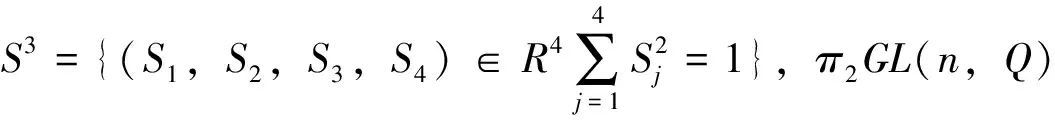
故假设不成立,则任意四元数矩阵至少有一个在Q上的左特征值.
定理3[2]λ∈Q为A∈Qn×n的一个左特征值⟺λ为A重特征多项式FA(λ)的根.
注:①笔者知道四元数矩阵的左,右特征值没有必然联系,则由定理1和定理3知,四元数矩阵的重特征多项式和拟特征多项式也没有必然联系.
② 由于A的拟特征多项式与右特征值都与A的复表示阵Ac有密切联系,故由复数域C上矩阵理论知四元数矩阵A的拟特征多项式与右特征值都是相似变换的不变量.但重特征多项式与左特征值都不是相似变换的不变量,但加上一定的限制条件笔者有如下定理:
定理4 若A∈Qn×n为自共轭阵,则A的左,右特征值统一,此时FA(λ)=FAc(λ).
证: 设A=A1+A2jA1,A2∈Cn×n,则由引理1知AH=A1H-A2Tj,由于A=AH,则:
设λ=λ1+λ2j(λ1,λ2∈C是A的任一右特征值,则存在0≠α∈Qn×1,s.t.Aα=αλ另设:
α=α1+α2j(α1,α2∈Cn×1且不全为0)⟹(A1+A2j)(α1+α2j)=(α1+α2j)(λ1+λ2j),
由引理1,上式左右两边可化简为:
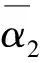
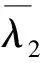
由复分解式的唯一性得:
(1)
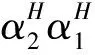
(2)
由于
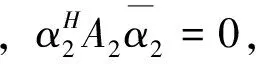
(3)
将方程组(3)第1个矩阵方程取共轭转置,注意到A1=A1H,再用第2个矩阵方程去减,得:
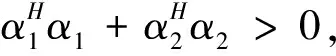
显然,若λ∈R,且存在0≠α∈Qn×1,使Aα=αλ则Aα=αλ=λα故λ也为A的左特征值.即A的左,右特征值统一,则由定理1和定理3知FA(λ)=fAc(λ).
[1]李文亮.四元数矩阵[M].长沙:国防科技大学出版社,2002.32.
[2]李样明.四元数矩阵理论中的几个概念间的关系[J].数学学报,1998,41(3):583.
[3]Fuzhen Zhang. Quaternions and matrices of quaternions linear algebra and its applications[J]. Linear Algbra and its Applications,1997,251(15):21.
[4]陈福元.四元数矩阵的右特征值[J].龙岩师专学报,1997,15(3):9.
[5]DR Fwenick. The spectral theorem in quaternions linear algebra and its applications[J].2003,371(14):75.
(责任编辑李平)
2013年度武汉市属高校教学研究项目(编号 2013132)成果。
2014-1-13
黄莉,ihuangli@foxmail.com。
O 151.2
A
1674-9545(2014)02-0056-(03)
