居民阶梯电价评定的定量分析*
2014-09-04朱家明李春忠
王 惠 朱家明 李春忠
(安徽财经大学统计与应用数学学院 安徽蚌埠 233030)
居民阶梯电价评定的定量分析*
王 惠 朱家明 李春忠
(安徽财经大学统计与应用数学学院 安徽蚌埠 233030)
针对山东省阶梯电价的制定,对相关数据进行boxcox变化、正态化、无量纲化及均值化的处理,结合正态分布曲线,运用概率、等距抽样、阈值、回归拟合等方法,建立合适梯度电价标准、用水用电量一元回归等模型,使用Matlab、Excel等软件编程,得出居民用电量所属档次、制定合理的阶梯电价新标准、用电量随用水量变化等结论。
阶梯电价,boxcox变化,正态分布法,Matlab
居民阶梯电价制度是利用价格杠杆促进节能减排的又一次实践。阶梯式电价把用户平均用电量设置为若干个阶梯分段或分档次定价计算费用。通过划分一、二、三档电量,较大幅提高第三档电量电价水平,可以在促进社会公平的同时,也培养全民节约资源、保护环境的意识,逐步养成节能减排的习惯。本文旨在探究用水量与用电量之间的关系并且制定合适的阶梯电价实施标准。本文基于相关数据和文献,对山东省的阶梯电价进行评价和定价。
1 居民用电阶梯电价的评价
1.1 模型的分析
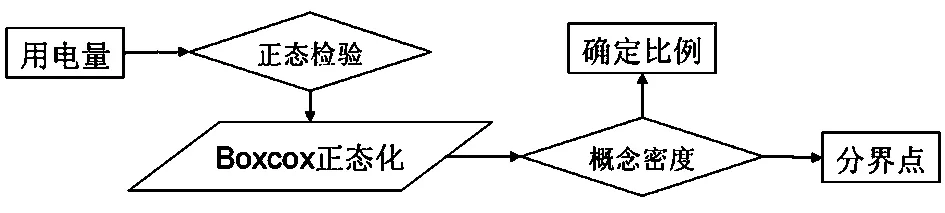
根据山东省济南市某两个小区的用水用电量统计表,结合山东省现行的阶梯电价标准,通过对地区A、地区B用电量数据的分析,定量判断两小区用电量属于第一档(ti≤210度)、第二档(210 图1 三个不同档次的阶梯电价计费标准 采用对数据正态化处理后建立概率密度分布函数的方法,得到两小区用电量水平在三个档次中所占的比例,进而判断出用电量所属档次,建模流程图如图2。 图2 居民用电量所属档次的判断和阶梯电价的制定 1.2 模型的准备 表1 A地区、B地区中用户编号1-10月的平均用电量数值表 表检验的h、p数值表 图的qq图 表检验的h、p数值 图的qq图 1.2.3现行阶梯电价标准变换后的对应值 山东省现行阶梯电价的三个档次所对应的数据经boxcox变换后得到三个档次的新标准,具体结果如下: A地区第一档次新标准:tAi≤20.50;B地区的第一档次新标准:tBi≤5.35; A地区第三档次新标准:tAi>27.71;B地区第三档次新标准:tAi5.99; 1.3 模型的建立与求解 各地区经过变换处理后的月平均用电量xAi、xBi的概率密度分布函数为[1]: (1) 其中,j=A,B;i=1,2,3,… 运用Excel软件分别计算出A地区、B地区月平均用电量的期望和标准差[2],解得: 则xAi、xBi的概率密度分布函数表达式为: (2) (3) 按照现行山东省的阶梯点检标准可以计算出A、B地区用电量水平在三个档次中所占的比例,计算公式如式⑷所示: (4) 其中,j=A,B;i=1,2,3…;r=1,2,3 解得: 对数据结果以及图5、图6进行分析,pA1 图5 A地区用电正态密度曲线图 图6 B地区用电正态密度曲线图 2.1 模型的分析 利用上述所建的电量归属档次模型,采用正态分布曲线求出各地区各自用电量覆盖率80%、95%分别对应的用电量,此电量即为合理的阶梯电价分界点。 2.2 模型的建立 第一档基本用电,电量按照覆盖80%居民的用电量来确定,第二档正常用电量则按照覆盖至95%的居民用电量。采用正态分布曲线[2]分别求出各地区各自用电量覆盖率80%、95%分别对应的用电量 (5) (6) 2.3 模型的求解 运用Matlab软件中morminv命令,得不同档次对应的月均用电量,结果如下 xAa=19.22,xAb=23.60xBa=5.33,xBb=5.93 (7) 解得tA1=183.25,tA2=283.19,tB1=207.01,tB2=375.10 (8) 在此,假设两个小区的每一档次中,单位电价按照山东省现行的电价收取,综上所述,可以总结出合适的阶梯电价实施标准如表4所列: 表4 合适阶梯电价实施标准相关参照值 3.1 对问题的分析 研究小区的居民用水与用电量之间是否有关系。季节不同,人们的日常生活中用水与用电量存在差异。将用水、用电量无量纲化后,建立回归模型,并对求解的结果进行经济和统计意义上两个层面的检验。 3.2 模型的准备 初步判断,居民用水与用电量符合经济意义,本模型采用等距抽样的方法从286个样本中选取出96个样本进行问题的研究分析。采取阈值法分别对各区每季度的用水与用电量的原始数据无量纲化处理,数学表达式如式⑼,部分数据如表5所示。 (9) 表5 A小区居民年无量纲化平均用水量与用电量 3.3模型的建立与求解 图7 A小区居民年平均用水量与用电量的折线图 从折线图中可以大致的判断出居民的平均用水量与平均用电量之间存在着正相关关系。所以可以建立居民平均用水与平均用电量之间的一元回归模型,具体数学模型表达式为: yA=aAxA+bA (10) 根据所建立的模型,运用Matlab软件[5]计算出参数,并做出一元回归拟合的图形如图8所示,具体结果如下: aA=1.0056,bA=-0.00112,aB=0.6631,bB=0.1511 (11) 图8 A小区yA与xA的一元回归拟合图 根据参数值以及拟合后图形的分析,可以解得小区居民的用水量与用电量之间的一元回归方程为: yA=1.0056xA-0.00112 (12) 由模型的求解可见,用量与用水量之间有很强的关系,且用电量是随着用水量的上升而增加。 3.4 对模型的检验 3.4.1经济意义检验x表示居民年平均用水量,用电量应该会随着用水量的增加而增加,符合所估计的模型,用电量y是随着用水量x的上升而增加。 3.4.2统计检验 模型的拟合优度检验,决定系数R2=0.9862。判定系数不仅反映了模型拟合程度的优劣,而且有直观的经济意义:它定量描述了被解释变量的变化中可以用回归模型来说明的部分,即模型的可解释程度。所建模型中R2=0.9862,这意味着用水量的变化引起用电量的波动,有98.62%可以通过所估计的模型来解释。 本文在解决不同问题时都巧妙地将杂乱无章的原始数据进行了合理化的处理,使得建立的模型更为直观。建立了阶梯电价标准模型和用水用电量回归模型,制定出了合理的阶梯电价,检验了模型的有效性,同时建立了居民用水量与用电量之间关系的模型,对在实际生活中制定合适的阶梯电价标准提供了参考。 [1]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2011.16. [2]张焕明.统计学实验教程[M].天津:天津大学出版社,2009.83. [3]冯莉.阶梯电价的评价与优化[J].经济管理者,2013,29(9):228. [4]朱柯丁,宋艺航,谭忠富,等.居民生活阶梯电价设计优化模型[J].华东电力,2011,39(6):862. [5]吴礼斌,闫云侠.经济数学实验与建模[M].天津:天津大学出版社,2009.30. (责任编辑胡安娜) Quantitative Analysis of the Assessment of Residential Electricity Price Ladder WANG Hui, ZHU Jiaming, LI Chunzhong (School of Statistics and Institute of Finance, Anhui University of Finance and Economics, Bengbu, Anhui 233030,China) Aimed at the enactment of price ladder in Shandong province, we analyzed the relevant data, processing with boxcox, normalization, non-dimensionalization and equalization as well as other methods. Besides, we built the model of appropriate gradient electricity price standards and water-power consumption monadic regression, and combined the normal distribution curve, meanwhile, and applied various techniques, such as probability, interval sampling and threshold value as well as regression fitting. Finally, we successfully drew the conclusion of the level that residents’ electricity consumption lies in, and set out the new reasonable standards of price ladder, and figured out how the electricity consumption changes over the water consumption and so on with the help of software program such as Matlab and Excel. price ladder,boxcox change, normal distribution, Matlab 国家自然科学基金项目(编号61305070),安徽财经大学教研项目(编号acjyzd201429)成果之一。 2014-4-1 王惠,1357694265@qq.com。 F 426.61,F 224 A 1674-9545(2014)02-0027-(05)
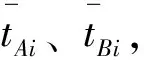

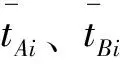
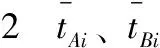


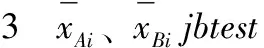

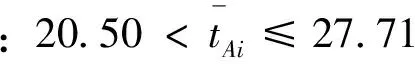
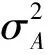
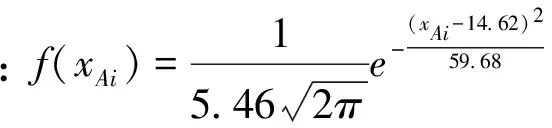
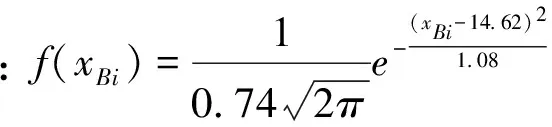




2 阶梯电价的优化设制


3 居民用水与用电量回归分析



4 小结
