一种基于页岩损伤规律的井壁坍塌压力确定方法
2014-09-04程万,金衍,陈勉,徐彤,陈刚
程 万, 金 衍, 陈 勉, 徐 彤, 陈 刚
(1.中国石油大学(北京)石油工程学院,北京 102249;2.油气资源与探测国家重点实验室(中国石油大学(北京)),北京 102249)
页岩地层的岩石力学性质受到多种因素的影响[1-2],与其他类型岩石相比并没有明显的规律性。研究表明,页岩的破坏主要受微裂缝、围压的影响,有劈裂式、单剪切式和双剪切式等3类破坏模式[1],而目前国内外预测井壁坍塌压力常用的Mohr-Coulomb准则(以下简写为M-C准则)仅适用于发生剪切破坏的井壁,不适宜用于页岩储层井壁坍塌压力的预测。大量研究证实,页岩内部发育有大量微裂缝,因此有必要从损伤力学的角度研究井壁围岩破坏规律。为此,笔者基于最小耗散能原理[3]和损伤力学[4],建立了页岩损伤力学模型,并以具有代表性的塔里木盆地群库恰克地区地层岩心为研究对象,室内研究了损伤阈值应变与应变能密度之间的关系,并从页岩损伤破坏的角度给出了维持井壁稳定的最低钻井液密度,为预测页岩地层井壁坍塌压力提供了一种新方法。
1 页岩损伤力学模型的建立
在石油钻井中,钻开井眼改变了原地应力场的分布,井壁围岩中的裂缝在受到钻井液、井下管柱等因素的扰动后易缓慢扩展,引起岩石的局部损伤。由断裂损伤力学[4]可知,当损伤达到一定程度后岩石会发生宏观破坏。比如页岩地层,若在应力场作用下发生各向同性损伤,则当损伤累积到一定程度后就会造成页岩破坏。根据最小耗散能原理[3],任何耗能过程都将在与其相应的约束条件下以最小耗能的方式进行。岩石材料的损伤破坏本质是一种耗能过程[5],根据损伤力学基本理论[4],外荷载作用下材料内部某点发生的破坏耗能过程可认为是其损伤变量D由0到1的过程。在常三轴应力作用下,单位体积岩石的各向同性损伤能耗率为[3]:

岩石发生损伤破坏时,轴向应力等于抗压强度,并根据最小耗能原理和拉格朗日乘子法,可得:
(2)
岩石损伤后,垂向应力在加载过程中满足:
μσc
(3)
根据页岩常三轴全应力-应变曲线,在峰值应力(抗压强度)处,存在如下关系:
(4)
页岩损伤演化方程为:
(5)
当D=0时,可得损伤阈值应变为:
(6)
当轴向应变大于损伤阈值应变时,应力-应变曲线服从以下关系:
μσc
(7)
当轴向应变趋于无穷大时,损伤变量趋于极值:
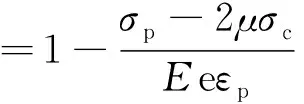
(8)
2 页岩常三轴抗压试验
塔里木盆地群库恰克地区页岩地层井壁失稳问题突出[6],且具有一定的典型性和代表性。选取该地区埋深4 500~4 800 m地层的6块标准岩心(φ25.0 mm×50 mm,圆柱体),采用中国石油大学(北京)岩石力学实验室设计组建的深水孔隙压力伺服试验系统,进行了岩心单轴和三轴抗压试验。垂向加载速度恒定不变,岩石轴向应变率等于1.167 2×10-5,损伤常数λ恒等于2.334 4。表1为岩心试验参数及测试结果。
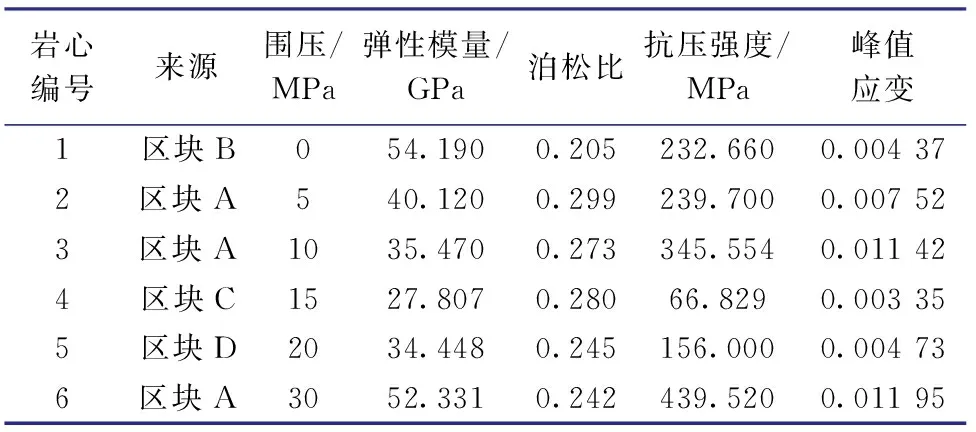
表1 页岩岩心试验参数及测试结果Table 1 Test parameters and results of shale core samples
根据表1中数据,绘制了岩心1—6不同围压下的应力-应变曲线,见图1。
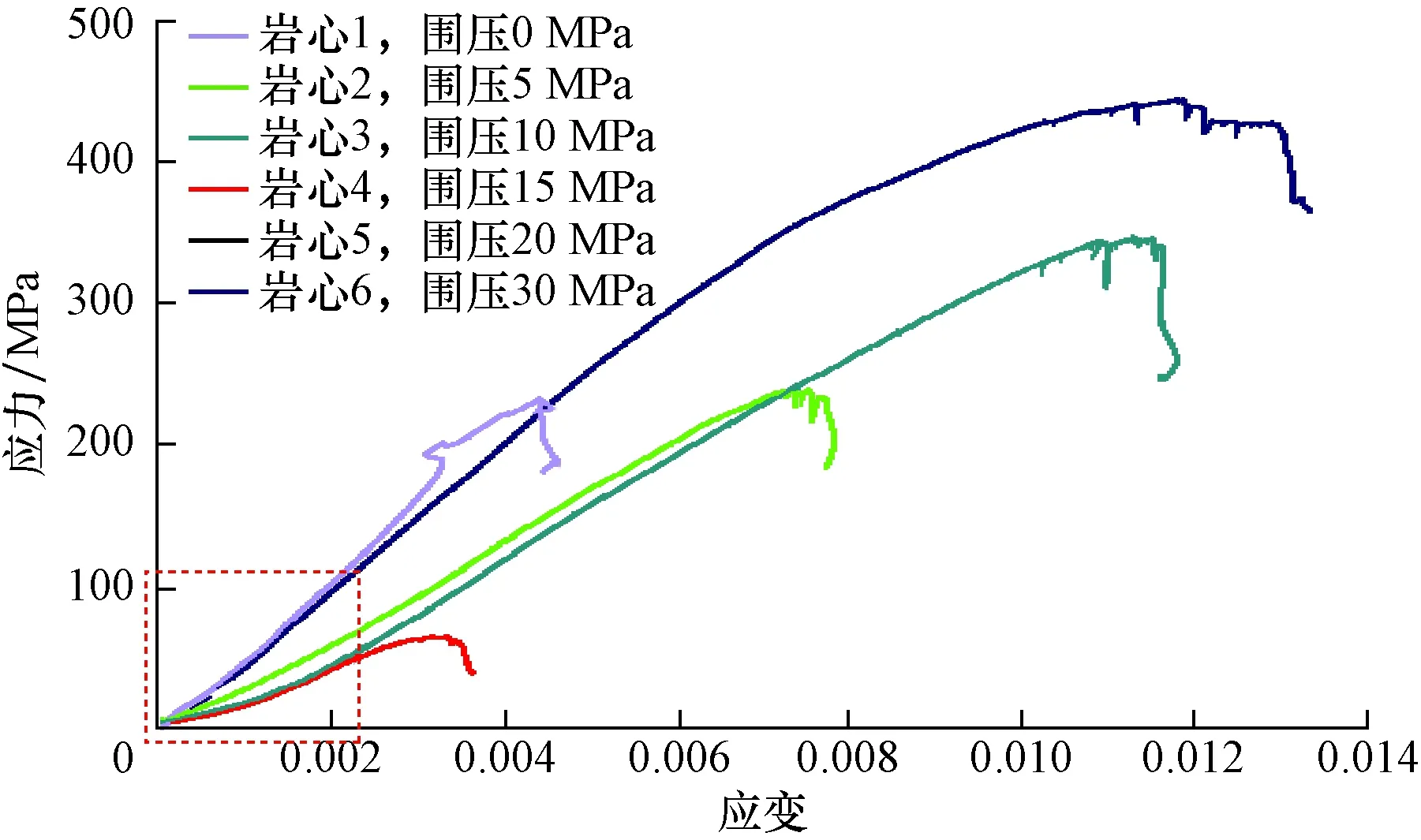
图1 不同围压下页岩的应力应变曲线Fig.1 Stress-strain curves of shale under different confined pressure
由图1可知:泊松比、弹性模量、抗压强度随围压的变化无明显规律;虚线框内曲线有向下凹的趋势,表明页岩内部存在很多原生微裂缝,在轴向压缩下原生微裂缝首先发生闭合。钻井中,这些微裂缝易因应力扰动而缓慢扩展,造成局部损伤。
参考式(5)—(7),研究岩心1—6的应力-应变曲线,可得到损伤阈值应变、极限损伤变量、损伤演化方程;又由页岩应力-应变曲线可知,页岩达到损伤阈值应变时开始损伤,并迅速发生破坏,表现出较强的脆性,此时损伤度-应变曲线服从线性规律,由此可给出初始损伤演化方程。岩心1—6的损伤方程见表2。
根据表2数据,绘制了岩心1—6的损伤度-应变曲线,见图2。图中,实线1—6为岩心1—6的损伤演化方程对应的损伤度-应变曲线,实线与横轴截距为损伤阈值应变。倾斜的虚线a—f分别为岩心1—6的初始损伤演化方程对应的损伤度-应变曲线。

表2 页岩岩心1—6的损伤方程Table 2 Damage equations of shale cores No.1 to No.6
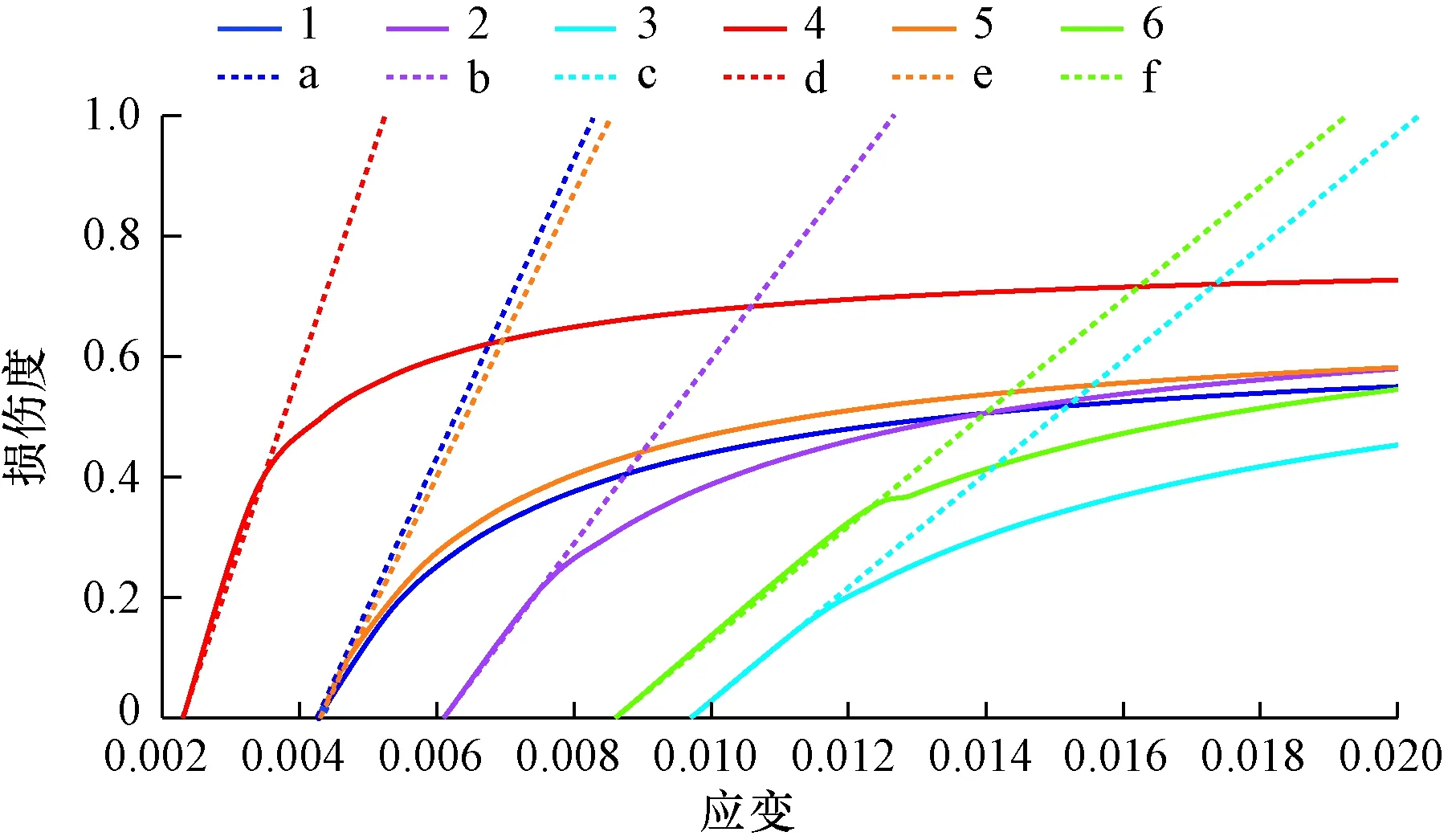
图2 岩心1—6的损伤度应变曲线Fig.2 Damage strain curve of core No.1 to core No.6
以岩心2、岩心3为例,比较试验得到的应力-应变曲线与理论推导的应力-应变曲线,结果如图3所示。

图3 试验所得与理论所得应力应变曲线的比较Fig.3 Comparison of testing and theoretical stress-strain curves
由图3可知:损伤发生之前,轴向应力-应变关系服从弹性力学本构方程;损伤发生后,轴向应力-应变关系服从损伤演化方程;考虑页岩初始损伤演化的应力-应变曲线与室内试验所得曲线吻合较好。
3 最低安全钻井液密度的确定
3.1 确定方法
采用表1数值可计算出岩心1—6的应变能密度[7],并绘出应变能密度与破坏时的应变、损伤阈值应变之间的关系曲线(见图4)。由图4可知,破坏时的应变、损伤阈值应变随应变能密度增大而增大。
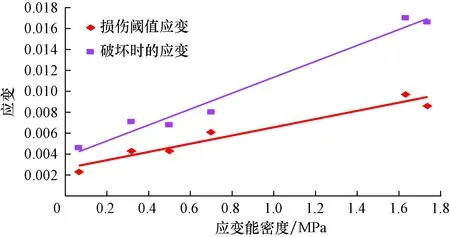
图4 岩心1—6的应变与应变能密度关系Fig.4 Strain versus strain energy density of core No.1 to core No.6
采用线性拟合,得到了应变能密度与破坏时应变的线性方程(9)和应变能密度与损伤阈值应变的线性方程(10):
U=128.365εf-0.461
(9)
U=256.410 3ε0-0.666 7
(10)
由于页岩在达到损伤阈值应变后迅速发生破坏,可将损伤阈值应变作为岩石损伤破坏的临界应变值。根据直井井壁围岩三向主应力[8-9]和应变能密度,可比较出三向主应力中的最大值及其应变,并根据式(10)得到维持井壁稳定的最低钻井液密度。
3.2 实例说明
忽略孔隙压力对井壁围岩应力的影响,并假设井壁不可渗透。最大水平主应力为正北方向,井深5 000 m,上覆岩层压力梯度为2.23 MPa/100m,最大水平应力梯度为2.09 MPa/100m,最小水平应力梯度为1.56 MPa/100m,弹性模量40 GPa,泊松比0.2,黏聚力7.5 MPa,内摩擦角为25°[8]。依据前述方法,可得不同方位角下维持井壁稳定的最低钻井液密度(见图5)。
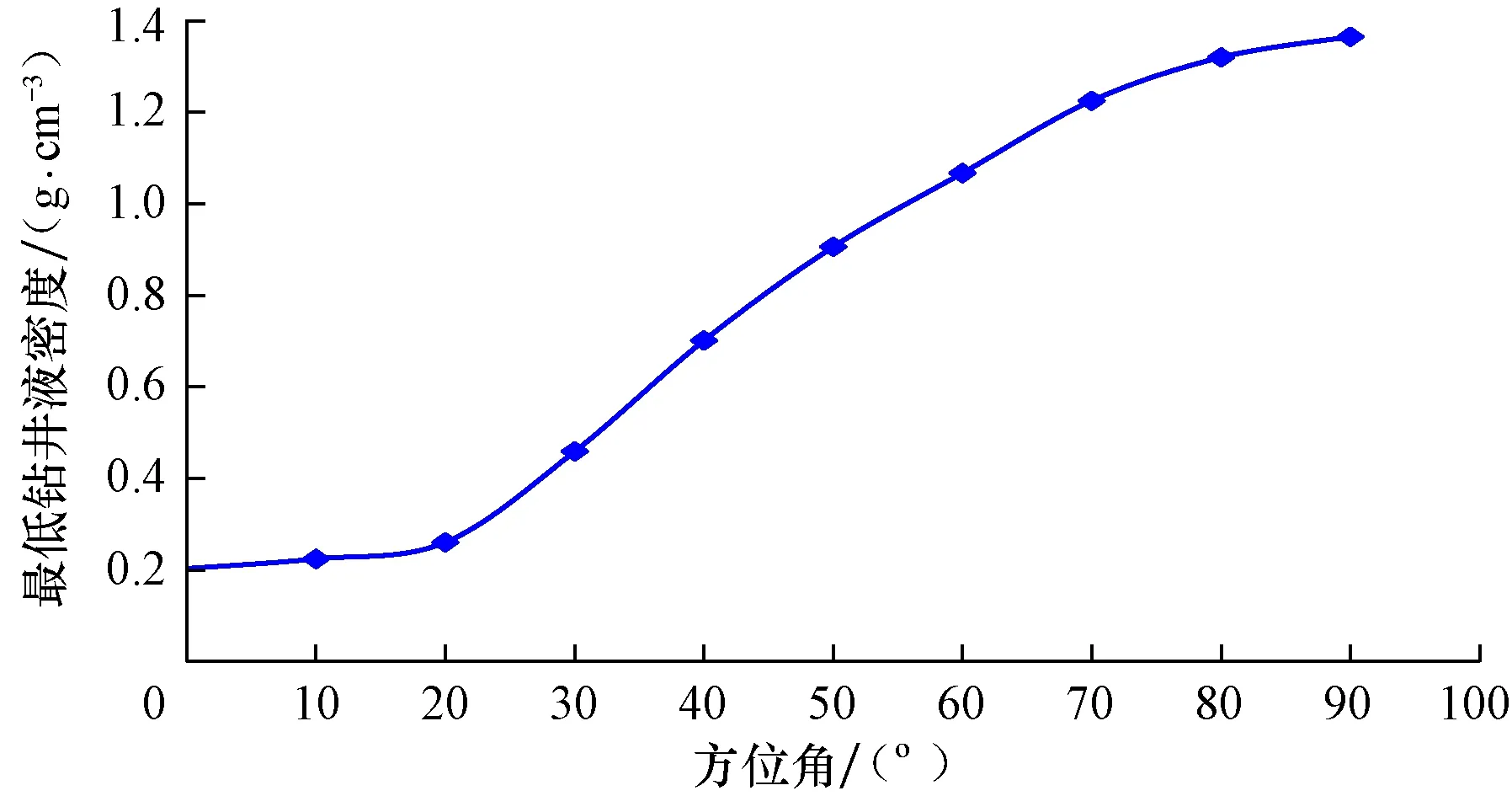
图5 不同方位角下维持井壁稳定的最低钻井液密度Fig.5 The minimum density of drilling mud to keep wellbore stable
由图5可知,方位角在0~90°时,最低钻井液密度值随方位角增大而增大,故取钻井液密度最大值1.365 g/cm3作为维持该段井壁稳定的坍塌压力当量密度。根据M-C准则计算的坍塌压力当量密度为1.348 g/cm3,略小于利用前述方法的计算值。目前,安全钻井液密度窗口[8-9]的上限常依据地层破裂压力或漏失压力确定,下限常以M-C准则设计的坍塌压力剖面或地层孔隙压力剖面为基准。钻井液密度如果低于前述方法计算的坍塌压力当量密度,井壁岩石就容易超过损伤阈值,微裂缝缓慢扩展,引起井壁局部发生损伤,当损伤累积到一定程度后, 容易导致井壁岩石破坏,引发井壁失稳。
4 结论与认识
1) 基于最小耗散能原理和损伤力学,推导出了页岩损伤演化方程、损伤阈值应变值和极限损伤变量值,初始损伤理论曲线与室内试验曲线吻合较好,损伤阈值应变、破坏时应变均随应变能密度的增大而增大,线性关系良好。
2) 应用损伤阈值应变与应变能密度的线性关系,可计算出维持页岩地层井壁稳定的最低钻井液密度,从而得出井壁坍塌压力。
3) 实例计算表明,依据损伤规律设计的页岩地层井壁坍塌压力略大于依据M-C准则计算出的坍塌压力,这容易使依据后者设计的钻井液密度难以防止井壁发生损伤,从而更容易导致井壁失稳。
符号说明
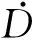
参考文献
References
[1] 李庆辉,陈勉,金衍,等.页岩气储层岩石力学特性及脆性评价[J].石油钻探技术,2012,40(4):17-22.
Li Qinghui,Chen Mian,Jin Yan,et al.Rock mechanical properties and brittleness evaluation of shale gas reservoir[J].Petroleum Drilling Techniques,2012,40(4):17-22.
[2] 李庆辉,陈勉,金衍,等.页岩脆性的室内评价方法及改进[J].岩石力学与工程学报,2012,31(8):1680-1685.
Li Qinghui,Chen Mian,Jin Yan,et al.Indoor evaluation method for shale brittleness and improvement[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(8):1680-1685.
[3] 高玮,汪磊,杨大勇.基于能量原理的岩石损伤研究[J].地下空间与工程学报,2010,6(增刊2):1672-1677.
Gao Wei,Wang Lei,Yang Dayong.Study on the rock damage evolution based on energy principle[J].Chinese Journal of Underground Space and Engineering,2010,6(supplement 2):1672-1677.
[4] 张行.断裂与损伤力学[M].北京:北京航空航天大学出版社,2009:318-360.
Zhang Xing.Fracture and damage mechanics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2009:318-360.
[5] 高玮,汪磊,杨大勇.岩石损伤演化的能量方法研究[J].岩石力学与工程学报,2011,30(增刊2):4087-4092.
Gao Wei,Wang Lei,Yang Dayong.Rock damage evolution based on energy principle[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(supplement 2):4087-4092.
[6] 谢水祥,蒋官澄,陈勉,等.破解塔里木盆地群库恰克地区井壁失稳难题的钻井液技术[J].天然气工业,2011,31(10):68-72.
Xie Shuixiang,Jiang Guancheng,Chen Mian,et al.Drilling fluid technology in preventing the wellbore instability in the Qunkuqiake Area,Tarim Basin[J].Natural Gas Industry,2011,31(10):68-72.
[7] 杨桂通.弹塑性力学引论[M].北京:清华大学出版社,2004:49-52.
Yang Guitong.Introduction to elasticity and plasticity[M].Beijing:Tsinghua University Press,2004:49-52.
[8] 金衍,陈勉.井壁稳定力学[M].北京:科学出版社,2012:21-35.
Jin Yan,Chen Mian.Wellbore stability mechanics[M].Beijing:Science Press,2012:21-35.
[9] 陈勉,金衍,张广清.石油工程岩石力学[M].北京:科学出版社,2008:57-66.
Chen Mian,Jin Yan,Zhang Guangqing.Rock mechanics related to petroleum engineering[M].Beijing:Science Press,2008:57-66.
