编织结构复合材料热膨胀性能的影响因素

(天津工业大学纺织学院，天津，300387)

复合材料具有高模、高强及良好的损伤容限等突出的力学特性，尤其是具有可设计性强的优点，因此可以应用在建筑、体育、医疗等众多领域。近年来，复合材料还被广泛应用于航天航空领域。若材料发生变形，就会影响材料的使用性能、安全性以及使用寿命。对于如航天器等工作在极端温度中的材料，要求在一定温度场内的变形应趋近于零。热膨胀系数作为表征材料热稳定性的重要参数，对复合材料的性能影响很大。例如，在低温或高温环境下工作的复合材料，为研究其热应力和热稳定性问题，必须了解复合材料的热膨胀特性；又如，复合材料大都在高温条件下固化成型，在室温下使用时材料内部存在一定的残余应力，对残余应力的分析也依赖于热膨胀性能。由此可以看出，对复合材料热膨胀性能的研究意义重大。

1 复合材料的热膨胀性能

复合材料一般包括基体和作为增强体材料的纤维。在温度变化时，由于基体与纤维的热膨胀系数不同，纤维和基体之间会产生内应力，因此复合材料的“膨胀”是综合变形的结果。在选择基体和增强体材料时，应兼顾其热膨胀性能和其他性能。例如，被视为航天器中颇具前途的高性能烧蚀材料碳基复合材料具有烧蚀热高、烧蚀率低、高温力学性能优良等特点[1]，而作为胶黏剂的环氧树脂，也要求其具有较低的热膨胀系数。复合材料的热膨胀性能与它的许多其他性能一样，可以根据其组分材料性能、纤维铺设和纤维含量等参数, 进行理论计算和设计[2]。碳纤维/环氧树脂编织复合材料在特殊环境(如温度场中)具有良好的尺寸稳定性，尤其可以通过选择性能互补的基体、纤维，并与纤维编织结构、纤维体积分数等因素的调节相结合，实现特定方向上的零热膨胀，使其在精密仪器、宇航等高精端工程技术中显示独特优势[3]。

2 影响热膨胀性能的因素

复合材料的热膨胀性能对适用于不同温度环境下仍能保持高度尺寸稳定的结构设计影响极大，材料零膨胀的实现是多个因素综合的结果。

2.1 原料

设计低膨胀材料要从选择原料开始，在选择基体与增强体材料时应当兼重其热膨胀性能。选用受温度影响小的树脂基体和使用高模量纤维，可以降低树脂基体对复合材料性能的影响。一般青睐于选择热膨胀系数较低的材料与负膨胀材料复合。

飞机材料结构中应用的增强纤维有碳纤维、芳纶、玻璃纤维和硼纤维等。碳纤维由于具有高强高模、低密度的优点，在力学性能、工业化生产、品种和应用等方面，技术日趋成熟，遥遥领先于其他新材料。芳纶的性能虽然尚佳，但在湿热状态下力学性能明显降低，一般不用作飞机主要承力结构，多与碳纤维混合使用；芳纶受紫外线辐射时强度大幅度下降，使其在太空中的应用受到制约。玻璃纤维刚度低，只用于一些次要结构。硼纤维直径大且刚硬，成形和加工艰难，成本较高，应用很少。碳纤维的热膨胀系数很低，接近于零，在400 ℃以下的温度范围内较为稳定。碳纤维的热膨胀系数沿不同方向存在差异，在纤维轴向具有负的温度效应，即随温度的升高，碳纤维有收缩的趋势，可制成零膨胀复合材料。碳纤维沿纤维轴向线膨胀系数为(-0.9～-0.72)×10-6/℃，垂直纤维轴向线膨胀系数约为(22～32)×10-6/℃[4]。表1对比了几种目前在复合材料中应用较广泛的高性能纤维的热膨胀系数。

表1 几种常用高性能纤维线膨胀系数对比[4] [单位：(10-6·℃-1)]

基体起着支撑、保护纤维并传递载荷的作用，其性能对复合材料相关的力学性能有决定性的影响。在复合材料中常用的基体树脂有酚醛、聚酯、环氧和有机酸树脂，其线膨胀系数分别为(60～80)×10-6/℃、(80～100)×10-6/℃、60×10-6/℃和308×10-6/℃[4]。环氧树脂具有形式多样、固化方便、力学性能优良、化学稳定性强、收缩性低及黏附力强等特点，具有正的热膨胀系数。显然，环氧树脂与碳纤维热膨胀系数的分布特征是设计零膨胀结构的必要条件[3]。

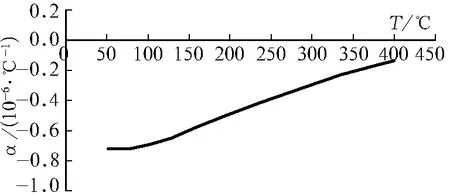
图1 碳纤维热膨胀曲线[5]

图1为碳纤维的热膨胀曲线。由图1可以看出，碳纤维具有高温负膨胀的性能，在400 ℃以下碳纤维的热膨胀系数为负，依据趋势可以推断出温度超过450 ℃时平均热膨胀系数为正。同时可以发现，碳纤维的热膨胀系数与温度变化几乎呈线性关系[5]。 赫玉欣等[6]对环氧树脂的热膨胀曲线进行了研究，得出了环氧树脂在玻璃化温度以下热膨胀变形很小，显示为正膨胀的结论。根据零膨胀设计理念，碳纤维和环氧树脂结合制作的复合材料能够满足“材料受热近零膨胀”的要求。

研究发现，混杂纤维复合材料比单一纤维复合材料具有更宽广的零膨胀设计范围[7]。同时，也有大批的学者通过对树脂的改性来改善复合材料的热膨胀系数。赫玉欣等[6]采用聚对苯二甲酸丁二醇酯(PBT)、聚碳酸酯(PC)和聚醚酰亚胺(PEI)三种热塑性塑料对环氧树脂进行改性，研究这三种热塑性塑料对环氧树脂基体热膨胀系数的影响。结果表明：三种热塑性塑料均可提高环氧树脂的玻璃化转变温度；用PBT、PEI和PC改性的纯环氧树脂在玻璃化转变温度下的热膨胀系数分别降低了14.99%、17.44%和23.96%，而当温度高于玻璃化转变温度后热膨胀系数均高于纯环氧树脂。张清杰等[8]应用TDE-85 和AFG-90三官能度环氧树脂，配合芳香胺固化剂，研制了一种适合于国产T-300 碳纤维复合材料缠绕成型的耐高温树脂基体。测试结果表明，其浇铸体有良好的耐热性能和力学性能。在缠绕成型方面有大量关于基体改性的研究。黎昱等[9]在BS-1(TDE-86环氧树脂和潜伏性固化剂BF3·MEA按一定比例配制)基础上，加入反应活性较低的固化剂，调节其反应活性。该基体材料在室温下黏度低，低黏度平台范围宽，对纤维具有良好的润湿性，与高模量碳纤维匹配性良好，能较充分地发挥高模量碳纤维的性能。

2.2 编织参数

编织结构复合材料的热膨胀特性除了与纤维、基体自身热物理性能有关外, 还与纤维编织体的编织参数(如编织角、编织形状、编织单元大小以及纤维体积分数等)有关。为达到改善膨胀性能、调节热膨胀系数和实现零膨胀结构的目的，调节以

上各因素之间的相对关系也是一种重要手段[3]。

2.2.1 纤维体积分数

复合材料的热膨胀系数与纤维含量和组分膨胀系数有关，满足混合规则。由于碳纤维的热膨胀系数比环氧树脂的热膨胀系数低，所以热膨胀系数相对较大的基体体积含量越高，材料的热膨胀系数越大。此外，在材料热膨胀过程中，纤维束和基体的界面处产生较大的热应力，纤维束制约了基体的膨胀，纤维束含量越多，约束作用越显著，所以碳纤维体积含量越高，材料的热膨胀系数就会越低[10]。

姚学锋等[3]通过实验验证得出了在编织角固定的条件下，特别在编织角为35°、纤维体积分数为35%时，碳纤维/环氧树脂编织结构复合材料的膨胀系数为0，而纤维体积分数为54%时其膨胀系数均为负值的结论。若要求材料在某一方向上具有较低的膨胀，可以增加排布在该方向上的纤维[11]。

2.2.2 编织角和编织结构

在纤维体积含量一定时，增大编织角，热膨胀系数呈现增长的变化趋势，膨胀变形就会加剧。姚学峰等[3]对纤维体积含量固定、编织角介于30°～60°之间的二维和三维碳纤维/环氧树脂复合材料进行研究，得出了编织角为35°时材料实现零膨胀的结论。此外，成玲[12]对不同编织结构复合材料进行研究，发现不同编织结构的复合材料编织方向上的热稳定性不同，三维五向编织结构复合材料编织方向的热膨胀系数比三维四向编织结构复合材料编织方向的热膨胀系数更小。

2.2.3 纤维伸直状态

采用斜角编织方法编织，经纱呈现弯曲状，使其不能够完全发挥平直状态下的性能。当基体和纬纱膨胀时，经纱受拉应力产生被拉直的趋势，从而削弱其对材料膨胀的束缚作用[13]。由于直线状的纤维在直线方向上是不容易膨胀的，所以应使低膨胀方向上纤维尽可能伸直，减少交织降低纱线的弯曲。

2.2.4 界面性能与孔隙

复合材料的热膨胀变化规律是纤维和基体共同牵制作用的结果。因此，在对复合材料的热膨胀性能进行分析时，不能单纯地考虑增强体和基体的物理性能，必须兼顾增强体/基体界面状况。界面黏结状态对纤维复合材料不同方向的热膨胀系数影响程度不同，对纵向的影响远大于对横向的影响，黏结强度越高的材料热膨胀系数越小[14]。

材料中残留孔隙的存在总是不可避免的，且材料密度越小，孔隙率越高。一旦材料暴露于空气中，材料中的残留孔隙将会吸收大量的水分。当复合材料受热时，材料内的水分被蒸发，孔隙收缩，材料表现为负膨胀。孔隙率越高，吸水量越大，材料受热时产生的收缩越大，热膨胀系数就会更小。

3 材料热膨胀系数的研究方法

国内外学者对复合材料热膨胀性能的主要研究方法集中在对热膨胀系数的预测及实验测试两方面。其中，对热膨胀系数的预测又可分为理论预测与有限元预测两类。

理论预测是基于复合材料组分力学属性与几何参数，进而研究复合材料宏观性能的一种方法，包括混合定律(ROM)、Turner模型、Kerner模型、Schapery方法、CB方法、CH方法、桥联模型(BM)、RH方法、能量法、均匀化理论和遗传算法等。能量法是利用能量等效原理，将含有基体和纤维的非均质体等效成理想的连续均质体，由各组分的性能求解出复合材料整体的等效性能。

理论预测已经非常成熟，也取得了很多的成果。曹俊等[15]利用遗传算法研究了给定铺层设计的层合板满足低膨胀要求的铺层顺序优化。Schapery[16]利用能量理论，得出了具有各向同性组分复合材料的纵向和横向热膨胀系数的表达式。Pramila[17]根据原料的热弹性系数推导出了平衡对称角铺设层合板热膨胀系数的表达式，研究了热膨胀系数的零值和极值。Ganesh等[18]和Naik等[19]考虑了织物的二维结构特性及织物中的间隙，研究了织物几何参数对材料面内热膨胀性能的影响，建立了二维模型。梁军等[20]利用细观力学的Eshelby和Mori-Tanaka理论，预报了不同微裂纹密度下不同纤维体积分数碳纤维/ 环氧复合材料的有效热膨胀系数，研究了纤维与微裂纹间的相互作用、纤维体积含量对热膨胀系数的影响。熊璇等[21]基于细观力学利用桥联矩阵对单向复合材料的热膨胀系数计算公式进行理论推导，并用Msc.PATRAN和NASTRAN两种有限元预测软件建立有限元模型进行分析验证。刘书田等[22]利用均匀化方法，研究了空心材料和单向纤维复合材料的热膨胀行为，建立了组分材料性能、体积分数与热膨胀系数之间的关系，预测结果与理论分析、实验结果吻合。石连升等[23]利用一种无需对材料进行热应力分析的细观力学模型计算热膨胀系数，该模型只需知道在某一相关外力场作用下, 其组分相内部的平均应力场问题。

有限单元法作为结构力学位移法的拓展，其基本思路就是将复杂的结构看成由有限个单元仅在节点处连接的整体。首先，对每一个单元分析其特性，建立物理量之间的相关联系；然后，依据单元之间的联系，再将各单元组装成整体，从而获得整体性方程；再应用方程相应的解法，即可完成整个问题的分析。这是一种化整为零又集散为整和化未知为已知的方法，已被用作一个重要的研究工具。

Soheil[24]考虑了三维织物内部不同的纤维结构，建立有限元方法预测其热膨胀系数，将预测结果与层合板的结果进行对比。李剑峰等[25]通过有限元方法预报了6种复合材料的横向和纵向热膨胀系数，并将预报结果与理论分析及实验结果对比，均能很好吻合，得出了纵向热膨胀系数的变化趋势均是随着纤维体积含量的增大而单调减小，而纤维模量与基体模量之比对于横向热膨胀系数的影响却较为显著的结论。冉治国等[26]发展了一种探究连续纤维增强的复合材料热膨胀性能的随机扰动模型。该模型综合考虑了单向复合材料横截面上纤维的分布情况以及随机模型的真实周期性边界条件等，并针对高纤维体积含量的随机模型提出了随机扰动法(RDM)，RDM 方法可以处理的最大纤维体积分数不小于65%。

对比各预测方法，复合材料横向热膨胀系数的预测误差均大于纵向热膨胀系数的预测误差。ROM模型和Kerner模型的预测值均大于实测值。ROM模型考虑的因素最少，最为简单；Kerner模型更好地考虑了材料内部复杂的应力状况，与实测值相对接近。利用RDM模型可以提高预测效率，便于材料研究和工程应用。每种研究方法都有其不足，通常是将理论方法与实践相结合，先通过理论计算或有限元预测，再利用测试实验进行验证，使结果更真实。

4 结语

复合材料的热膨胀变化规律是纤维和基体相互限制、相互竞争的结果。从众多学者的研究结果可以看出，复合材料的零膨胀通过设计是可以实现的，各种理论预测方法与有限元的预测结果均能很好地吻合。编织结构复合材料的热膨胀性能不仅与纤维、基体自身的热物理性质、刚度系数相关, 还与编织体的编织模式以及纤维在材料中的伸直状态、纤维含量等参数有关。因此，可以通过调节各参数之间的相对关系，引入第二类高性能纤维或对基体材料进行改性处理的方法，来达到改善复合材料热膨胀性能以及按设计要求对其热膨胀系数进行调节的目的，进而使零膨胀结构的优化设计得以实现。

但目前有关复合材料热膨胀系数的研究依然存在一些问题。例如：孔隙率和纤维伸直状态对复合材料热膨胀系数的影响都只是定性的结论，并没有做出定量分析；对影响因素的研究尚不够深入，各种预测方法与测试的实测值都存在一定的误差。上述问题还需要在今后作进一步的研究。例如，热膨胀系数预测值与实测值之间误差的产生主要是因为建立的模型不能将复合材料中存在的孔隙、杂质的影响有效地模拟出来，更忽略了基体与增强体结合情况及加工缺陷的影响。建议可以尝试推测出预测值与实测值之间的一个相关系数来解决该误差问题。

[1] 易法军,张巍,孟松鹤，等.C/C复合材料高温热物理性能实验研究[J].宇航学报,2009,23(5):85-88.

[2] 张汝光.[(±45°)m/0°2n]s 层板的热膨胀性能和零膨胀的设计[J].玻璃钢/复合材料,1999(1):3-7.

[3] 姚学锋,杨桂,姚振汉，等.编织结构复合材料热膨胀特性的实验研究[J].复合材料学报,2000，17(4):20-25.

[4] 王汝敏,郑水蓉,郑亚萍.聚合物基复合材料及工艺[M].北京:科学出版社,2004：54-102.

[5] 欧阳国思,许路,刘成民，等.几种纤维的热膨胀系数实验测定[J].宇航材料工艺,1988(4):48-53.

[6] 赫玉欣,张丽,姚大虎，等.热塑性塑料对环氧树脂热膨胀系数的影响研究[J].化工新型材料,2012,40(3):117-120.

[7] 佟丽莉,陈辉.混杂纤维复合材料热性能特异性研究[J].纤维复合材料,1997,19(13):19-21.

[8] 张清杰,隋刚,杨小平.国产T-300 碳纤维湿法缠绕用耐高温环氧树脂基体[C]//中国复合材料学会.第十届中日复合材料学术会议论文集,2012:46-49.

[9] 黎昱,陈维强.缠绕成型复合材料壳体及基体改性研究[J].宇航材料工艺,2009(5):61-64.

[10] 陈盛洪.细编穿刺C/C复合材料热物理性能的模拟研究[D].哈尔滨：哈尔滨工业大学,2008.

[11] 吴海,曹英斌.低膨胀C/SiC复合材料设计与制备研究[C]//复合材料:创新与可持续发展(下册).北京:中国科学技术出版社,2010:943-947.

[12] 成玲.碳/环氧编织复合材料热膨胀特性分析[J].固体火箭技术,2010,33(1):108-111.

[13] 张彪,郭景坤.[NZP]陶瓷零膨胀性能的设计[J].材料研究学报,1996(1):39-44.

[14] 严学华,杨新波,程晓农.近零膨胀 ZrW2O8/ZrO2(Al2O3)复合材料的制备与性能[J].稀有金属材料与工程,2008,1(37):615-618.

[15] 曹俊,朱如鹏.层合板热膨胀系数优化设计的遗传算法实现[J].玻璃钢/复合材料,2003(2):33-35.

[16] SCHARPERY R A. Thermal expansion coefficients of composite material based on energy principles[J]. Composite Material ,1968,2(3):380-404.

[17] PRAMILA A. Thermal expansion of a balanced symmetric laminate[J]. Journal of Composite Materials,1990,24(7):786-794.

[18] GANESH V K, NAIK N K. Thermal expansion coefficients of plain-weave fabric laminates[J]. Composites Science and Technology,1994,51(3):387-408.

[19] NAIK N K, GANESH V K. Prediction of on-axes elastic properties of plain weave fabric composites[J]. Composites Science and Technology,1992,45(2):135-152.

[20] 梁军,杜善义,许兴利,等.含缺陷纤维增强复合材料热膨胀系数预报[J].哈尔滨工业大学学报,1997,29(3):36-38.

[21] 熊璇,吕国志,吕毅.细观力学法预测单向复合材料的有效热膨胀系数[J].强度与环境,2008,35(2):24-30.

[22] 刘书田,程耿东.基于均匀化理论的复合材料热膨胀系数预测方法[J].大连理工大学学报,1995,35(5):451-457.

[23] 石连升,刘红兵,王彪.预报复合材料热膨胀系数的细观力学模型[J].材料科学与工艺,1997,5(1):5-7.

[24] SOHEIL M. Predictions for coefficients of thermal expansion of three-dimensional braided composites[J]. AIAA Journal,1997,35(1):141-144.

[25] 李剑峰,燕瑛.复合材料热膨胀性能的细观分析模型与预报[J].北京航空航天大学学报,2013(8):1-7.

[26] 冉治国,燕瑛,李剑峰,等.复合材料热膨胀性能预报的随机扰动模型与实验验证[J].复合材料学报,2013(6):215-220.