基于线圈串套模型的粘扣带剥离、剪切强度力学模型研究

(1. 东华大学纺织面料技术教育部重点实验室，上海，201620；2. 无锡百和织造股份有限公司，无锡，201101)

粘扣带是由钩面粘扣带和毛面粘扣带成对组成的。毛面粘扣带的毛圈是由锦纶6复丝织成的小圈然后起毛而成，钩面粘扣带的钩是由锦纶66单丝织成小圈后切钩而成。钩面、毛面粘扣带一碰触便结合在一起，一扯便分开，并能反复使用，故其常作为紧固件产品来使用，方便快捷。粘扣带作为紧固件产品，其力学性能的好坏直接影响其质量的优劣[1]。粘扣带的力学性能主要包括剥离强度和剪切强度，为了从理论上计算或预测粘扣带的剥离强度和剪切强度，为粘扣带的力学性能评价提供依据，本文以针织线圈串套模型为基础，建立了粘扣带剥离强度和剪切强度力学模型，并通过实际测试和修正，获得了较准确的粘扣带剥离强度和剪切强度计算式。

1 粘扣带剥离强度力学模型

粘扣带单钩强力力学模型是粘扣带剥离强度力学模型的基础，建立达里多维奇和米哈依洛夫针织线圈串套模型，通过对串套线圈的受力分析得到粘扣带单钩强力的计算式，然后以此为基础求得粘扣带剥离强度的计算式。

1.1 粘扣带单钩剥离强力力学模型

1.1.1 粘扣带剥离分离过程

实际使用中，粘扣带通过钩面的钩与毛面的毛圈相互钩挂而粘合在一起。当粘扣带钩面和毛面剥离分开时，毛圈要从钩中滑出，此时产生的力就是剥离力。粘扣带实际粘合情况如图1所示。

粘扣带钩面与毛面的粘合比较复杂，现以达里多维奇和米哈依洛夫针织线圈串套模型为基础，建立粘扣带单钩剥离强力力学模型[2]。

假设粘扣带由毛面粘扣带上的毛圈套在钩面粘扣带上的钩上(不切钩)，靠摩擦力使钩面粘扣带和毛面粘扣带粘合在一起。模型中构成线圈的纱线直径为d，线圈圆弧为半圆，其半径为r，粘扣带的单钩剥离力等于串套线圈分离时的摩擦力，由此可得到粘扣带单钩剥离强力的力学模型。粘扣带的钩和毛圈相互串套和完全分开(剥离)的过程如图2所示。

1.1.2 线圈串套模型下粘扣带单钩受力分析

根据达里多维奇和米哈依洛夫针织线圈串套模型得到线圈分离(粘扣带钩和毛圈剥离)时线圈(钩)的受力分析如图3所示。

图3中，F为线圈所受正压力，M为弯矩，fμ为线圈所受摩擦力。

图1 粘扣带钩和毛圈实际粘合情况

图2 粘扣带单钩串套模型及剥离过程

(a)针织线圈串套模型

(b)粘扣带单钩受力图3 针织线圈串套模型及粘扣带单钩受力分析

根据达里多维奇和米哈依洛夫针织线圈串套模型假设：

(1)平面结构的线圈由圆弧和直线形成，但在连接点直线与圆弧不相切；

(2)两线圈分离时是在圆弧的最宽处；

(3)纱线完全弹性变形；

(4)纱线弯曲时长度不变。

根据弹性力学理论，弹性杆上任一点的曲率与作用于该点处的弯矩成比例，即：

(1)

式中：θ——纱线上任一点T处的切线与x轴之间的夹角 (°)；

B——纱线弯曲刚度(cN·cm2)，B=EI；

I——截面惯性矩(cm4)，I=πd4/64；

E——锦纶66的弹性模量(cN/cm2)；

r——圆弧部分的半径(cm)；

d——锦纶66纤维直径 (cm)；

fμ——摩擦力(cN)；

M——在T点处的弯矩(cN·cm)，M=2fμ(r+d)；

dθ/ds——在T点处的曲率(cm-1)。

由于f=2fμ

(2)

根据式(1)和式(2)可得粘扣带单钩剥离力f为：

(3)

1.2 粘扣带单钩剥离强力力学模型参数的确定

因纤维的弹性模量只与纤维材料本身的性质有关，故弹性模量的值可以直接引用锦纶弹性模量的值[3]，即E=214.6 cN/tex。

由于σb=γPt×103

(4)

式中：σb——纤维断裂应力(cN/cm2);

γ——纤维密度(锦纶密度为1.14 g/cm3)；

Pt——纤维断裂强度(N/tex)。

则E=2.446×107cN/cm2。

取r=0.05 cm时，

(5)

用AI-7000S型拉力强度试验仪对粘扣带的单钩剥离强力进行测试。测试时把单个钩和单个毛圈钩挂在一起，拉伸时匀速垂直向上拉，当钩和毛圈完全分离时测得的力即为实测单钩的剥离强力fS，不同钩直径的粘扣带的实测剥离强力共测量20次，取其平均值。不同钩直径下粘扣带的单钩理论剥离强力与实测剥离强力见表1。

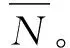
表1 锦纶粘扣带单钩理论剥离强力和实测剥离强力

(6)

1.3 粘扣带剥离强度力学模型的建立

粘扣带的剥离强度是指单位宽度内粘扣带的钩和毛圈分离所需要的力。假设粘扣带单位长度上的钩数为SB(钩/cm)，钩和毛圈钩挂在一起的数目占总钩数的百分比(即钩挂率)为ωB。由于粘扣带在剥离的过程中，某一排钩毛还未完全分离时，下一排的钩毛就开始分离，这样会对粘扣带的剥离强度产生影响。为了使计算式准确，需要引入修正系数KB对粘扣带剥离强度进行修正。最后得出整片粘扣带剥离强度PLB的计算式为：

PLB=KBωBSBfX=NKBωBSBf=0.65KBωBSBf

(7)

式中：KB——修正系数；

ωB——钩挂率(%)；

SB——钩密度(钩/cm)；

fX——修正的单钩剥离强力(cN)；

f——单钩的理论剥离强力(cN)。

1.4 粘扣带剥离强度模型的参数确定

实测由不同钩直径构成的锦纶粘扣带的宽度、钩数、钩密度和钩挂率，见表2。

为了使粘扣带剥离强度的计算式简单化，取钩

表2 粘扣带的宽度、钩密度和钩挂率

密度SB=6.5(钩/cm)，钩挂率ωB=76%。假设粘扣带在剥离过程中只有一排钩毛发生钩挂，即当前钩挂的钩毛剥离时，其前面一排的钩毛已完全分离，后面一排的钩毛尚未开始发生剥离，此时的修正系数取KB=1。当KB=1时，把以上参数代入式(7)，可得整片粘扣带的理论剥离强度PLB为：

(8)

参照GB/T 23315—2009中粘扣带剥离强度的测试方法[4]，把粘扣带裁剪成100 mm×25 mm，测试速度为300 mm/min，在AI-7000S型拉力强度试验机上测试其剥离强度。不同钩直径的粘扣带测量5组剥离强度，然后取平均值，结果见表3。

表3中的理论剥离强度PLB是把不同的钩直径值代入式(8)求得的。为了缩小理论剥离强度与实测剥离强度的差距，此处引用修正系数KiB=实测剥离强度PSB/理论剥离强度PLB。

表3 整片粘扣带的理论剥离强度、实测剥离强度及数据处理

PXB=2.8PLB

(9)

为了验证粘扣带剥离强度计算式的准确性，可通过计算剥离强度的偏差百分率WB来验证。

(10)

式中：PXB——修正后粘扣带的剥离强度;

PSB——实测粘扣带的剥离强度。

剥离强度的偏差百分率WB计算结果见表3。由表3可知WB<3% ，在较小的误差范围内，可以认为粘扣带剥离强度计算式的精确度较高，可以用作锦纶粘扣带剥离强度的计算式。最终粘扣带剥离强度的计算式PB为：

(11)

2 粘扣带剪切强度力学模型

此处所用到的粘扣带单钩强力的模型和计算式与上面粘扣带剥离强度模型中的单钩强力相同，可以直接引用。

2.1 粘扣带单钩剪切强力力学模型

2.1.1 粘扣带剪切分离过程

实际使用中，粘扣带通过钩面的钩与毛面的毛圈相互钩挂而粘合在一起。当粘扣带的钩面和毛面沿着长度方向剪切分开时，钩要从毛圈中滑出，此时产生的力就是剪切力。粘扣带实际钩挂及单钩剪切分离情况如图4所示。

粘扣带的钩和毛圈相互串套和完全分开(剪切分离)的过程为：初始状态下粘扣带的钩跟毛圈沿垂直于粘扣带平面方向相互串套，在受到粘扣带长度方向的力(剪切力)作用时，粘扣带的钩先把毛圈压倒，然后毛圈再从钩中脱离，最后钩与毛圈分开[5]。过程如图5所示。

2.1.2 粘扣带单钩剪切强力力学模型参数确定

粘扣带单钩剪切强力中的单钩受力分析及参数确定与粘扣带单钩剥离强力中的单钩受力分析及参数确定的过程相同，此处直接引用式(3)和式(5)。

2.2 粘扣带剪切强度力学模型的建立

粘扣带的剪切强度是指单位面积内粘扣带钩和毛圈在有效闭合区域内沿其长度方向上拉伸分离所需要的力。假设粘扣带单位面积上的钩数为SJ(钩/cm2)，钩和毛圈钩挂在一起的数目占总钩数的百分比(即钩挂率)为ωJ。由于粘扣带在剪切分离的过程中，某一排的钩毛分离后再继续跟下一排的钩毛粘合再分开，在分开粘合的过程中粘扣带的钩挂率会发生变化，这样会对粘扣带的剪切强度计算式产生影响。为了使计算式准确，需要引入修正系数KJ对粘扣带剪切强度进行修正。最后得出整片粘扣带剪切强度PLJ的计算式为：

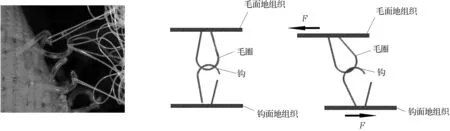
图4 粘扣带实际钩挂及剪切分离情况

图5 粘扣带单钩串套模型及剪切分离过程

PLJ=0.65KJωJSJf

(12)

式中：KJ——修正系数；

ωJ——钩挂率(%)；

SJ——钩密度(钩/cm2)；

f——单钩的理论剥离强力(cN)。

2.3 粘扣带剪切强度模型的参数确定

实测由不同钩直径构成的锦纶粘扣带的钩密度和钩挂率，见表4。

为了使粘扣带剪切强度计算式简单化，取钩密度SJ=53(钩/cm2)，钩挂率ωJ=98%，假设粘扣带参照GB/T 23315—2009中粘扣带剪切强度的测试方法 ，把粘扣带裁剪成100 mm×25 mm，有效闭合区域为50 mm×25 mm，测试速度为200 mm/min，在AI-7000S型拉力强度试验机上测试其剪切强度。不同钩直径的粘扣带测量5组剪切强度，然后取平均值[6]，结果见表5。

表4 粘扣带的宽度、钩密度和钩挂率

在剪切分离过程中，粘扣带钩挂率保持不变时，修正系数取KJ=1。当KJ=1时，把以上参数代入式(12)可得整片粘扣带的剪切强度PLJ为：

(13)

表5 整片粘扣带的理论剪切强度、实测剪切强度及数据处理

表5中，理论剪切强度PLJ是把不同的钩直径值代入式(13)求得的。为了缩小理论剪切强度与实测剪切强度的差距，此处引用修正系数KiJ=实测剪切强度PSJ/理论剪切强度PLJ。

为了验证粘扣带剪切强度计算式的准确性，可通过计算剪切强度的偏差百分率WJ来验证。

(14)

式中：PXJ——修正后粘扣带的剪切强度;

PSJ——实测粘扣带的剪切强度。

剪切强度的偏差百分率WJ计算结果见表5。由表5可知WJ<2% ，在较小的误差范围内，可以认为粘扣带剪切强度计算式的精确度较高，可以用作锦纶粘扣带剪切强度的计算式。最终粘扣带剪切强度的计算式PJ为：

(15)

3 结语

以达里多维奇和米哈依洛夫针织线圈串套模型为基础建立了粘扣带剥离强度和剪切强度力学模型，得出粘扣带单钩的强力计算式，并结合粘扣带综合钩挂率、钩密度得到整片粘扣带剥离强度和剪切强度的理论计算式。通过实际测量和系数修正，得到最终粘扣带剥离强度和剪切强度的计算式，并且偏差百分率分别小于3%和2%，可以用于粘扣带剥离强度和剪切强度的预测和计算。

[1] 李星,王其.粘扣带剥离强度力学模型研究[J].产业用纺织品,2011,29(10):19-22.

[2] 陈惠兰,冯勋伟.经编针织物线圈几何结构研究的进展[J].针织缝纫，1996,23(6):37-40.

[3] 于伟东.纺织材料学[M].北京:中国纺织出版社,2007.

[4] 全国纺织品标准化技术委员会.GB/T 23315—2009粘扣带[S].北京:中国标准出版社,2009.

[5] 赵磊.纬编针织物线圈的三维模拟及变形实现[D].武汉:武汉纺织大学,2011.

[6] 李星.粘扣带结构与力学性能研究[D].上海:东华大学纺织学院,2012.