二次规划问题的时滞投影神经网络模型的全局指数稳定
2014-09-04
(燕山大学理学院,秦皇岛 066004 中国)
1986年,Tank等[1]首次提出了解决线性规划问题的神经网络概念。 为保证网络收敛, Kennedy等[2-3]提出了改进的神经网络模型, 但只能得到近似解。基于对偶和映射理论, Xia等[4-6]提出了多种神经网络以精确求解二次规划问题。 文献[7]提出了利用线性投影神经网络解决二次规划问题,当M正定时,线性投影神经网络在平衡点是全局渐近稳定和全局指数稳定的。文献[8-10]提出了利用时滞投影神经网络解决二次规划问题,文献[11-12]提出用2个中立型时滞投影神经网络求解二次规划问题。
本文是对时滞投影神经网络模型求解二次规划问题的推广,此时滞投影神经网络没有罚参数和拉格朗日乘子,并给出了判断模型全局指数稳定的充分条件,它可以用于解决二次规划问题。
1 模型及预备知识
考虑如下凸二次规划问题:
(1)
其中:M是正定矩阵;A∈Rm×n是行满秩矩阵。
假设可行域x={x∈Rn|Ax=b,x≥0}非空且(1)存在最优解,下列2个投影神经网络可以解决问题(1):
(2)
(3)
其中:x(t)=φ(t),t∈[t0-τ,t0];α是大于零的常量;τ≥0表示传输延迟;投影算子PΩ:Rn→Ω定义为
(4)
本文提出了1个新的时滞投影神经网络模型解决问题(1):
(5)
其中:λ≥0是常数;x(t)=φ(t),t∈[t0-τ,t0];α是大于零的常量;τ≥0表示传输延迟;投影算子PΩ由(4)定义。
令Xe是(5)的平衡点,X*是(1)的最优解,X*是(5)的平衡点当且仅当X*是(1)、(2)、(3)的平衡点,因此Xe=X*。
为了方便以后的讨论,首先介绍一些定义和引理。
定义1[12]若对式(5)的任意初始点X0,∃k>0,η>0,使得
‖x-x*‖≤k‖φ-x*‖exp(-η(t-t0)),∀t≥t0成立,
其中‖φ(t0)-x*‖=supt0-τ≤t≤t0‖φ(t)-x*‖,则称时滞投影神经网络(5)在平衡点X*全局指数稳定。
引理1[12]∀x,y∈Rn,投影算子PΩ满足不等式
‖PΩ(x)-PΩ(y)‖≤‖x-y‖,
(PΩ(x)-PΩ(y))T(x-y)≥(PΩ(x)-PΩ(y))T(PΩ(x)-PΩ(y))
引理2[12](Gronwall不等式)设X(t)和Y(t)是定义在区间{t:t≥t0}上的非负实值连续函数,a(t)=a0(|t-t0|),其中a0(·)是单调递增函数,若

引理3[13]∀φ(t)∈C([-τ,0],Rn),若泛函微分方程(5)在区间[0,T]上存在满足初始条件的唯一连续的解x(t),并且x(t)在区间[0,T]上有界,则式(5)的解的存在区间可延拓到[0,+∞]上。
2 主要结果
定理1∀φ(t)∈C([-τ,0],Rn),时滞投影神经网络(5)在[0,+∞上存在唯一连续的解x(t)。
证明:令f(x(t))=-(1+λ)x(t)+λx(t-τ)+PΩ[(I-αM)x(t)-αq]+PΩ[(I-αM)x(t-τ)-αq],则
∀φ,φ∈C([-τ,0],Rn),由引理1得
‖f(φ)-f(φ)‖≤‖φ-φ‖+2‖I-αM‖‖φ-φ‖≤(3+2α‖M‖)‖φ-φ‖
故f在C上Lipschitz连续。根据泛函微分方程解的存在性定理,(5)在区间[0,T]上存在满足初始条件的唯一连续的解x(t)。设x*是神经网络(5)的一个平衡点。则
‖f(x(t))‖=‖f(x(t))-f(x*)‖≤
(1+λ)‖x(t)-x*‖+λ‖x(t-τ)-x*‖+
‖PΩ((I-αM)x(t)-αq)-PΩ((I-αM)x*-
αq)‖+‖PΩ((I-αM)x(t-τ)-αq)-PΩ((I-
αM)x*-αq)‖≤(1+λ)‖x(t)-x*‖+λ‖x(t-
τ)-x*‖+‖I-αM‖‖x(t)-x*‖+‖I-
αM‖‖x(t-τ)-x*‖≤(1+λ)‖x(t)-x*‖+
λ‖x(t-τ)-x*‖+(I+α‖M‖)‖x(t)-
x*‖+(I+α‖M‖)‖x(t-τ)-x*‖≤(2+λ+
α‖M‖)‖x(t)-x*‖+(1+λ+α‖M‖)‖
x(t-τ)-x*‖≤(2+λ+α‖M‖)‖x(t)‖+(1+λ+α‖M‖)‖x(t-τ)‖+(3+2λ+
2α‖M‖)‖x*‖


α‖M‖)‖x(s)‖+(1+λ+α‖M‖)‖x(s-
τ)‖+(3+2λ+2α‖M‖)‖x*‖]ds≤




2α‖M‖)‖x*‖T+(3+2λ+

由引理2,得
‖x(t)‖≤[(1+(1+λ+α‖M‖)τ)‖φ‖+(3+2λ+2α‖M‖)‖x*‖T]e(3+2λ+2α‖M‖)t≤
[(1+(1+λ+α‖M‖)τ)‖φ‖+(3+2λ+2α‖M‖)‖x*‖T]e(3+2λ+2α‖M‖)T<∞,t∈[0,T)
即x(t)在区间[0,T]上有界。根据泛函微分方程连续性定理,(5)在区间[0,T]上存在满足初始条件的唯一连续的解x(t)。
定理2令β=‖I-AT(AAT)-1A‖‖I-αM‖,若存在常数α>0,τ>0使得‖A‖e(1+λ)τ<1,e(1+λ)τ<2-β/4‖A‖+β,则时滞投影神经网络(5)在平衡点X*全局指数稳定。
证明:令x*是系统(5)的平衡点,则
λ(x(t-τ)-x*)+(PΩ((I-αM)x(t)-αq)-
PΩ((I-αM)x*-αq))+(PΩ((I-αM)x(t-τ)-αq)-PΩ((I-αM)x*-αq))=-(1+λ)(x(t)-x*)+λ(x(t-τ)-x*)+(I-AT(AAT)-1A)(g((I-αM)x(t)-αq)-g((I-αM)x*-αq))+(I-
AT(AAT)-1A)g((I-αM)x(t-τ)-αq)-g((I-αM)x*-αq)),由泛函微分方程的常数变易法,得
x(t)-x*=e-(1+λ)(t-t0)(φ(t0)-x*)+


AT(AAT)-1A)e-(1+λ)(t-s)(g((I-αM)x(s-
τ)-αq)-g((I-αM)x*-αq))ds
对∀t,存在整数N>0使得(N-1)τ≤t-t0≤Nτ。由上面的方程对任意整数0≤i≤(N-1)有

AT(AAT)-1A)e-(1+λ)(t-iτ-s)(g((I-αM)x(s)-αq)-g((I-αM)x*-αq))ds+

令β=‖I-AT(AAT)-1A‖‖I-αM‖,可得
‖g(x)-g(y)‖≤‖x-y‖,下面有
‖x(t)-x*‖≤e-(1+λ)(t-t0)‖φ(t0)-x*‖+

AT(AAT)-1A‖e-(1+λ)(t-s)‖g((I-αM)x(s)-αq)-

AT(AAT)-1A‖e-(1+λ)(t-s)‖g((I-αM)x(s-τ)-
αq)-g((I-αM)x*-αq)‖ds=


AT(AAT)-1A‖e-(1+λ)(t-s)‖g((I-αM)x(s)-αq)-
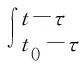
AT(AAT)-1A‖e-(1+λ)(t-s)‖g((I-
αM)x(s-τ)-αq)-g((I-αM)x*-αq)‖ds≤

αM‖‖x(s)-x*‖e-(1+λ)(t-s)ds+






由Gronwall不等式得
e(1+λ)t‖x(t)-x*‖≤e(1+λ)t0‖φ(t0)-
即
‖x(t)-x*‖≤‖φ(t0)-x*‖(1+
因此,(5)是全局指数稳定的。
3 仿真实例
通过实例验证二次规划问题解的有效性
考虑二次规划问题
其中取

则此问题有唯一解u*=(0.7496,0.6351)T。
取λ=2,α=0.1,τ=0.1,则(5)可化解为:
0.1M)x(t)-0.1q)+PΩ((I-0.1M)x(t-0.1)-0.1q) (6)
其中
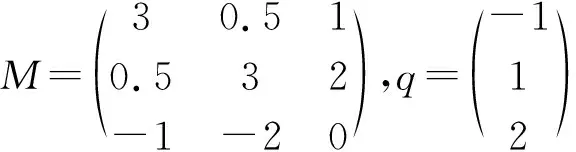
取初始函数φ(t)=[t,sin(t),1]T,(t∈[-1,0]),神经网络(6)收敛于其平衡点
x*=(u*,-1.6210)T
4 结论
本文提出了一种新的求解二次规划问题的时滞投影神经网络模型。利用泛函微分方程理论,证明了新模型解的存在唯一性,并给出了时滞投影神经网络全局指数稳定的充分条件。数值模拟表明该类网络模型不仅可行而且有效。
[1]Tank D W, Hopfield J J. Simple Neural Optimization Networks: An A/D Convert, Signal Decision Circuit, and a Linear Programming Circuit[J]. IEEE Trans on Circuits and Systems,1986,33(5): 533-541.
[2] Kennedy M P, Chua L O. Neural Networks for Nonlinear Programming[J]. IEEE Trans on Circuits and Systems,1988, 35(5): 554-562.
[3] Rodriguez-Vazquez A, Dominguez-Castro R, Rueda A, et al. Nonlinear Switch-capacitorNeural Networks for Optimization Problems[J]. IEEE Trans on Circuits and Systems, 1990, 39(3): 221-225.
[4] Xia Y S, Leng H, Wang J. A Projection Neural Network and its Application to Constrained Optimization Prob lems[J].IEEE Trans on Circuits and Systems, 2002, 49(4): 447-458.
[5] Xia Y S, Wang J. A General Projection Neural Network for Solving Monotone Variational Inequalities and Related Optimization Problems[J]. IEEE Trans on Neural Networks, 2004, 15(2): 318-328.
[6] Hu X L.Applications of the General Projection Neural Network in Solving Extended Linear Quadratic Programming Problems with Linear Constraints[J]. Neurocomputing,2009, 72(4/6): 1131-1137.
[7]Xia You-shen ,Wang Jun.A Recurrent Neural Network for Solving Linear Projection Equations[J]. Neural Network,2000,13(1):337-350.
[8]Liu Qing-shan,Cao Jin-de ,Xia You-shen.A Delayed Neural Network for Solving Linear Projection Equations and its Analysis[J].IEEE Tram on Neural Networks,2005,9(4):834-843.
[9]Yang Yong-qing , Cao Jin-de.Solving Quadratic Programming Problems by Delayed Projection Neural Network[J].IEEE Tram on Neural Networks,2006,11(17) :1630-1634.
[10]Liu Zi-xin,Lu Shu, Hong Shou-ming.A New Delayed Projection Neural Network for Solving Linear Variational Inequalities and Quadratic Optimization Problems[J].International Symposium on Computational Intelligence and Design,2008,9(8):1630-1634.
[11]Cheng C J, Liao T L,Yan J J, et al.Globally Asymptotic Stability of a Class of Neutral-Type Neural Networks with Delays[J].IEEE Trans sySt,Man,Cybcrn B,Cybem,2006,10(5):1191-195.
[12]Cheng Long,Hou Zcng-Guang, Tan Min.A Neutral-Type Delayed Projection Neural Network for Solving Nonlinear Variational Inequalities[J].IEEE Trans on Circuits Andsystems,2008,8(8):806-810.
[13]Hale J K,Verduyn Lunel S M.Introduction to Functional Differential Equations[M].New York:Springer,1993:235-242.
