耗散SRLW方程的一个三层加权线性差分格式

林雪梅，胡劲松，刘 倩

(西华大学数学与计算机学院 四川 成都 610039)

在研究弱非线性离子声波和空间带电波的传播时，文献[1]提出了正则长波(RLW)方程的对称描述，即对称正则长波(SRLW)方程：

uxxt-ut=ρx+uux

(1)

ρt+ux=0

(2)

并给出了方程(1)、(2)的双曲正割平方(sech2形式)孤立波解(v是速度，且v2>1)：

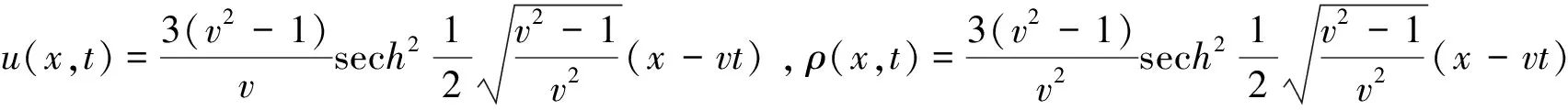
(3)

显然，SRLW方程(3)式关于x和t的导数是对称的，并且与描述浅水波及等离子漂移波的正则长波方程非常相似[2-3]。SRLW方程(1)、(2)、(3)式也出现在许多其他数学、物理领域[4-6]。数值考察表明其孤立波的相互作用是非弹性的[7]，因此，SRLW方程的孤立波不是孤立子。关于SRLW方程的定解问题的适定性及数值方法的研究也引起了广泛关注。郭柏灵在文献[8]中研究了一类广义SRLW方程周期初值问题解的存在性、唯一性和正则性，并得到了谱逼近解的误差估计。文献[9-16]分别用Fourier拟谱配点方法、拟谱方法、有限差分方法等研究了SRLW方程的初边值问题。

在实际问题中，粘性耗散是不可避免的，而且与色散一样起着十分重要的作用；因此，研究带有耗散的对称正则长波方程

uxxt-ut+βuxx=ρx+uux

(4)

ρt+ux=0

(5)

(其中β>0是耗散系数)是非常有意义的。在考虑耗散时，方程(4)、(5)是反映非线性离子声波运动本质现象的合理模型[17]。文献[17-21]分别讨论了方程(4)、(5)的解的适定性和整体存在唯一性，但其解析解很难求出，于是，研究方程(4)、(5)的定解问题的数值解就很有价值。文献[22-24]分别用有限差分方法和混合有限元方法讨论了一类带有阻尼项的耗散对称正则长波方程的初边值问题。

本文考虑方程(4)、(5)有如下的初始条件和边界条件：

u(x,0)=u0(x)，ρ(x,0)=ρ0(x)，x∈[xL,xR]

(6)

u(xL,t)=u(xR,t)=0，ρ(xL,t)=ρ(xR,t)=0，t∈[0,T]

(7)

不难证明，问题(4)—(7)具有如下守恒律：

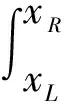
(8)

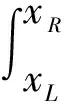
(9)

文献[25-26]分别研究了初边值问题(4)—(7)的差分近似解，并分别对其提出了一个具有二阶精度的两层非线性差分格式和三层线性差分格式，且三层线性差分格式在数值求解时不需要迭代，计算时间比较节省,但都没有考虑问题本身的守恒量。本文利用文献[27]处理Rosenau-RLW方程的技巧，引入加权系数θ，对问题(4)—(7)提出了一个加权平均隐式差分格式，合理地模拟了问题本身的2个守恒量(8)和(9)，通过适当地调整加权系数θ，从而使计算结果具有更高精度。

1 差分格式的守恒律和差分解的估计

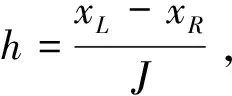
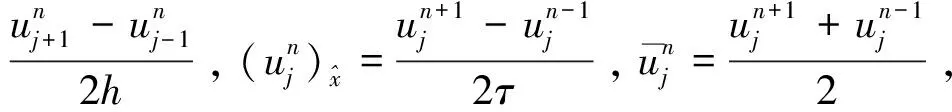
对问题(4)—(7)考虑如下的有限差分格式：

(10)

(11)

(12)

(13)

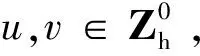
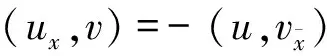
从而有

引理2[12](离散的Sobolev不等式[12])存在常数C1和C2，使得

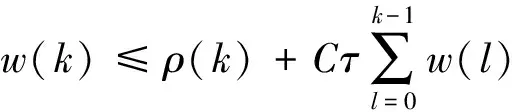
定理1 设u0∈H1，ρ0∈L2,则差分格式(10)—(13)关于以下离散能量是守恒的，即

(14)

(15)

证明： 将(10)式与h相乘，并对j从1到J-1进行求和，由边界条件(13)和引理1得

(16)

将(16)式递推可得(14)式。

同理，将(11)式与h相乘，并对j从1到J-1进行求和，得

(17)

将(17)式递推可得(15)式。

定理2 设u0∈H1，ρ0∈L2,则差分格式(10)—(13)的解满足：

‖un‖≤C,‖ρn‖≤C,‖un‖∞≤C,(n=1,2,…,N).

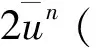
(18)

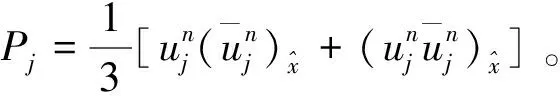
由边界条件(13)式，利用引理1,有

(19)

又

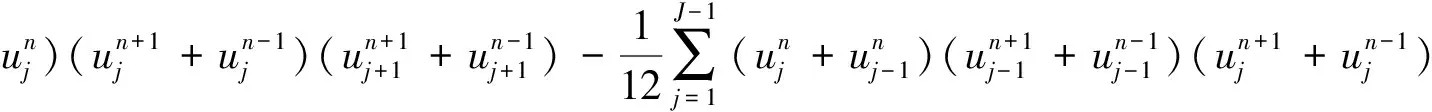
(20)

(21)

将(19)、(20)式代入(18)式并与(21)式作和，整理得

(22)

令

则由(22)式可得：

Bn≤Bn-1≤Bn-2≤…≤B0=C，又

所以

只要取足够小的τ，满足1-Cτ>0,就有

再由引理2，得

‖un‖∞≤C

2 差分格式的可解性

定理3 差分格式(10)—(13)是唯一可解的。

证明： 用数学归纳法。显然u0,ρ0是初值条件(12)式唯一确定的，再用两层格式[25]计算出二阶精度的u1,ρ1(即u0,ρ0和u1,ρ1是被唯一确定的)。假设u0,u1,…,un和ρ0,ρ1,…,ρn是唯一可解的，现在考虑方程(10)和(11)中的un+1和ρn+1，

(23)

(24)

将(23)式与un+1作内积，得

(25)

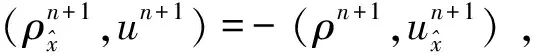
所以，(25)式即为

(26)

再将(24)式与ρn+1作内积，得

(27)

将(26)式与(27)式相加，得

也就是说，方程(23)和(24)仅有零解。因此，差分格式(10)—(13)中的un+1和ρn+1是唯一可解的。证毕。

3 差分格式的收敛性和稳定性

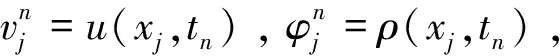
(28)

(29)

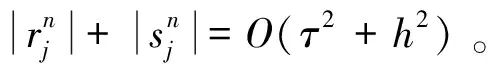
定理4 设u0∈H1，ρ0∈L2,则差分格式(10)—(13)的解un以‖·‖∞，ρn以‖·‖L2收敛到初边值问题(4)—(7)的解，且收敛阶为O(τ2+h2)。

证明： 用(28)式减去(10)式，(29)式减去(11)式，并记：

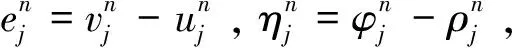
(30)

(31)

(32)

又因为

(33)

由引理1有

(34)

再用类似于(20)式的推导过程，有

(35)

由(33)—(35)式，得

由定理3以及Schwarz不等式，得

(36)

又

(37)

(38)

(39)

将(36)—(39)式代入(32)式,得

(40)

(41)

将(40)式与(41)式相加，有

(42)

令

‖ηn+1‖2+‖ηn‖2

则(42)式变为

Dn-Dn-1≤2τ‖rn‖2+2τ‖sn‖2+Cτ(Dn+Dn-1)

即

(1-Cτ)(Dn-Dn-1)≤2τ‖rn‖2+

2τ‖sn‖2+2CτDn-1

只要取足够小的τ，满足1-Cτ=δ>0,就有

(Dn-Dn-1)≤Cτ‖rn‖2+Cτ‖sn‖2+

CτDn-1

(43)

对(43)式从1到n求和，得

先用两层格式[25]计算出具有二阶精度的u1和ρ1，使之满足D0≤O(τ2+h2)2，由

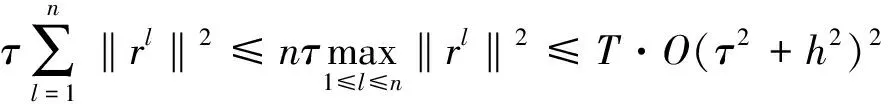
由引理3可得

Dn≤O(τ2+h2)2

即

再有引理2有

‖en‖∞≤O(τ2+h2)

证毕。

与定理4类似，可以证明：

定理5 在定理4的条件下，则差分格式(10)—(13)的解un以‖·‖∞，ρn以‖·‖L2稳定。

4 数值实验

在t=0时，由于耗散还没有产生，所以在数值实验中，我们把问题(4)—(7)中的初值函数取为SRLW方程(1)、(2)的初值函数(t=0时)：

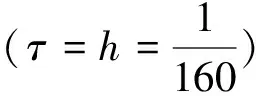
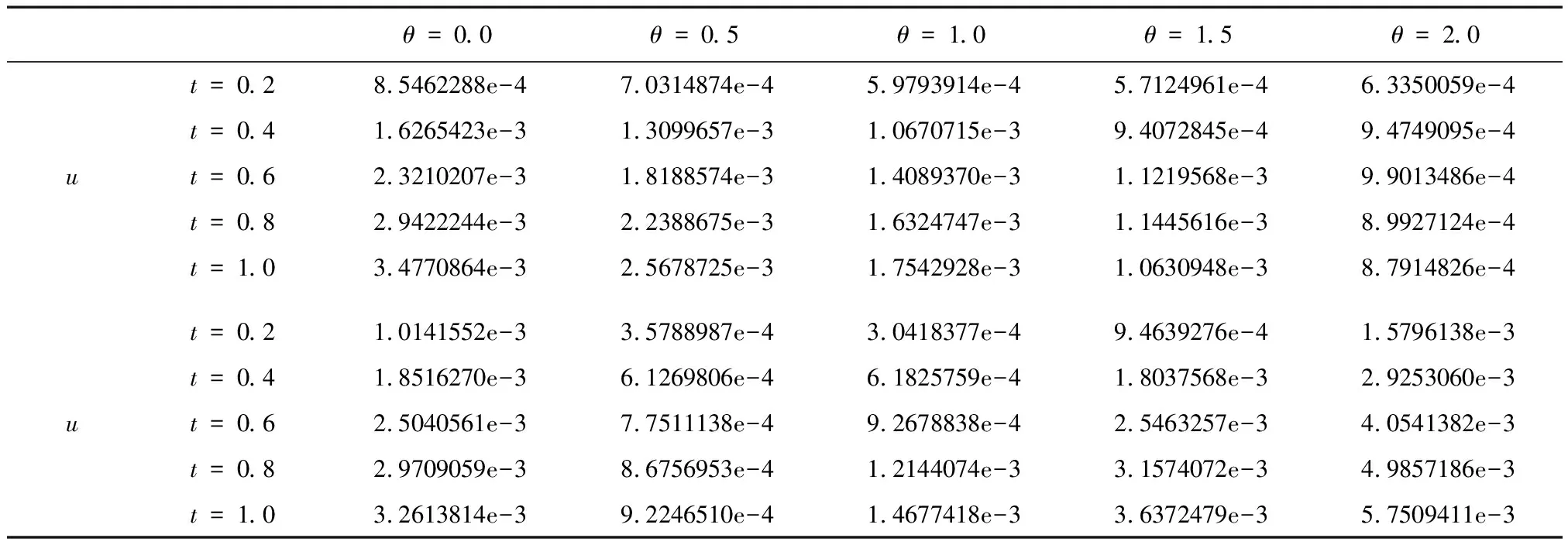
表1 τ=h=0.1时，就不同参数θ，在几个不同时刻的l∞误差

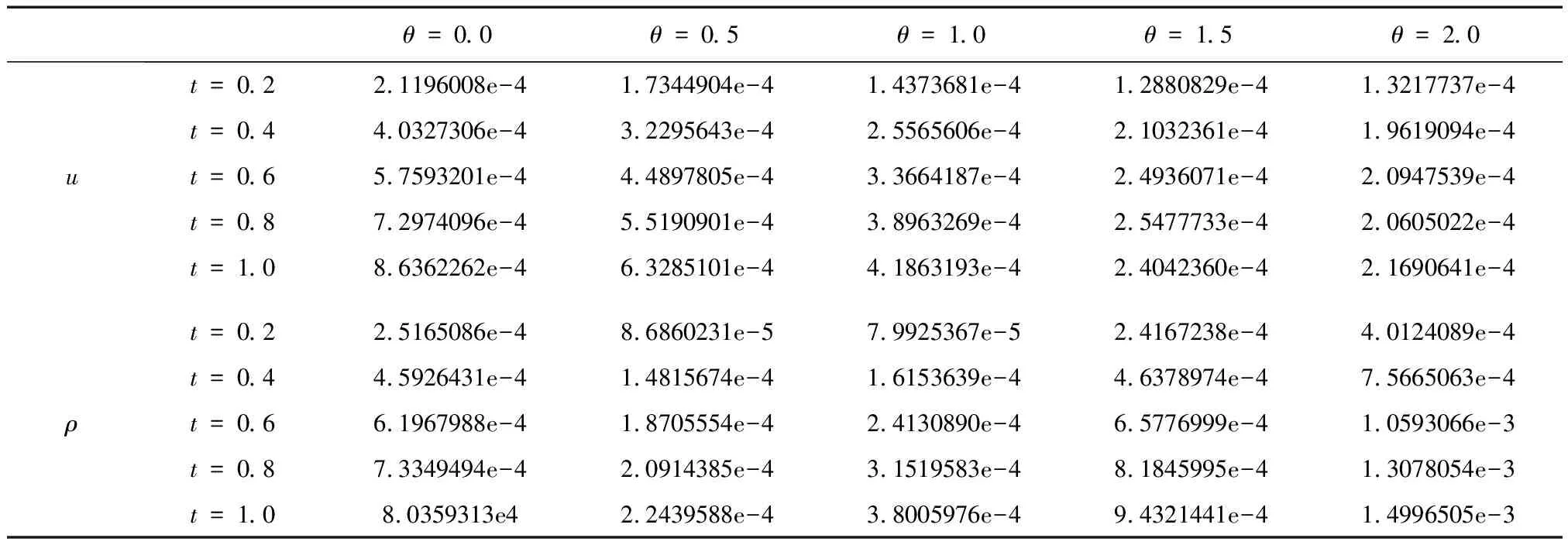
表2 τ=h=0.05时，就不同参数θ，在几个不同时刻的l∞误差

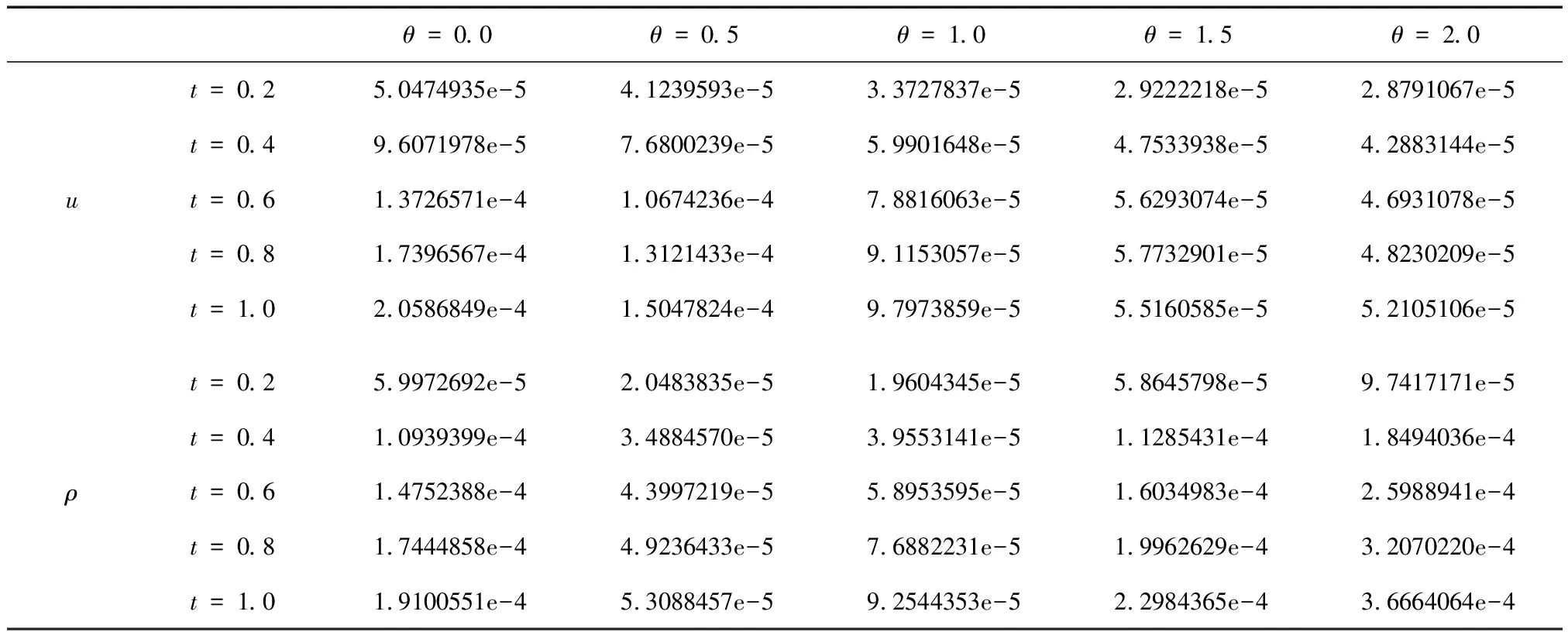
表3 τ=h=0.025时，就不同参数θ，在几个不同时刻的l∞误差

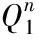
表4 在不同时刻对守恒量(8)和(9)的数值模拟和

表5 在不同时刻对守恒量(8)和(9)的数值模拟和

从数值算例可以看出，本文格式明显具有二阶精度，且适当地调整加权系数θ，可以大幅度提高计算的精度。另外，差分格式也合理地模拟了问题本身的2个守恒量，故本文对初边值问题(4)—(7)提出的差分格式(10)—(13)是有效的。

[1]Seyler C E, Fenstermacler D C. A Symmetric Regularized Long Wave Equation[J]. Phys Fluids, 1984, 27(1):4-7.

[2]Albert J. On the Decay of Solutions of the Generalized BBM Eqation[J]. J Math Anal Appl, 1989,141(2): 527-537.

[3]Amick C J,Bona J L,Schonbek M E. Decay of Solutions of some Nonlinear Wave Eqations[J]. J Diff Equs, 1989,81(1):1-49.

[4]Ogino T,Takeda S.Computer Simulation and Analysis for the Spherical and Cylindrical Ion-acoustic Solitons[J]. Journal of Physics Society of Japan,1976,41(1):257-264.

[5]Makhankov V G. Dynamics of Classical Solitons(in Non-integrable Systems)[J].Physics Reports,A Review Section of Physics Letters (Section C),1978,35C(1):1-128.

[6]Clarkson P A. New Similarity Reductions and Painleve Analysis for the Symmetric Regularized Long Wave and Modified Benjamin-Bona-Mahoney Epuations[J].J Phys A:Math Gen,1989,22(18):3821-3848.

[7]Bogolubsky J L. Some Examples of Inelastic Soliton Interaction[J].Comput Phys Comm, 1977,13(1):149-155.

[8]Guo Bo-ling. The Spectral Method for Symmetric Regularized Wave Equations [J]. J Comput Math, 1987, 5(4):297-306.

[9]郑家栋,张汝芬,郭本瑜. SRLW方程的Fourier拟谱方法[J].应用数学和力学，1989,10(9): 801-810.

[10]郑家栋.广义SRLW方程的拟谱配点方法[J].计算数学，1989,11(1): 64-72.

[11]尚亚东,郭柏灵.广义对称正则长波方程的勒让德和切贝雪夫拟谱方法[J].应用数学和力学，2005,26(4): 590-604.

[12]柏琰,张鲁明.对称正则长波方程的一个守恒差分格式[J].应用数学学报,2007, 30(2), 248-255.

[13]Wang Tingchun , Zhang Luming , Chen Fangqi . Conservative Schemes for the Symmetric Regularized Long Wave Equations[J]. Appl Math Comput, 2007，190: 1063-1080.

[14]王廷春,张鲁明.对称正则长波方程的拟紧致守恒差分逼近[J].数学物理学报,2006, 26A(7):1039-1046.

[15]王廷春,张鲁明,陈芳启. 对称正则长波方程的拟紧致守恒差分格式[J].工程数学学报,2008, 25(1)：169-172.

[16]柏琰,张鲁明.对称正则长波方程的一个新的守恒差分格式[J].应用数学,2009, 22(1):130-136.

[17]Guo Boling, Shang Yadong. Approximate Inertial Manifolds to the Generalized Symmetric Regularized Long Wave Equations with Damping Term[J]. Acta Math Appl Sinica, 2003, 19(2):191-204.

[18]Shang Yadong,Guo Boling,Fang Shaomei. Long Time Behavior of the Dissipative Generalized Symmetric Regularized Long Wave Equations[J]. J Partial Diff Eqs,2002(15):35-45.

[19]尚亚东,郭柏灵. 耗散的广义对称正则长波方程周期初值问题的整体吸引子[J].数学物理学报，2003,23A(6):745-757.

[20]尚亚东,郭柏灵. 带有阻尼项的广义对称正则长波方程的指数吸引子[J].应用数学和力学，2005,26(3):259-266.

[21]Fang Shaomei,Guo Boling,Qiu Hua.The Existence of Global Attractors for a System of Multi-dimensional Symmetric Regularized Long Wave Equations[J]. Commun Nonlinear Sci Numer Simulat, 2009, 14:61-68.

[22]Hu Jinsong , Xu Youcai , Hu Bing . A Linear Difference Scheme for Dissipative Symmetric Regularized Long Wave Equations with Damping Term[J]. Boundary Value Problems, 2010 (2010), Article ID 781750, 16 pages.

[23]Hu Jinsong , Hu Bing , Xu Youcai .C-N Difference Schemes for Dissipative Symmetric Regularized Long Wave Equations with Damping Term[J].Mathematical Problems in Engineering, 2011 (2011), Article ID 651642, 16 pages.

[24]Xu Y, Hu B , Xie X ,et al. Mixed Finite Element Analysis for Dissipative SRLW Equations with Damping Term[J]. Appl Math Comput,2012,218: 4788-4797.

[25]胡劲松,胡兵,徐友才. 耗散对称正则长波方程的有限差分逼近[J].计算数学,2011,33(2):177-184.

[26]胡劲松,胡兵,徐友才. 耗散对称正则长波方程的平均隐式差分格式[J].高等学校计算数学学报，2012,34(4):300-307.

[27]Pan X, Zhang L. On the Convergence of a Conservative Numerical Scheme for the Usual Rosenau-RLW Equation [J].Applied Mathematical Modelling,2012,36:3371-3378.