生产线模糊图像恢复的投影迭代算法和维纳滤波算法比较

许 强,谢维成,陈 佳,黄 超,张 雪

(西华大学电气信息学院，四川 成都 610039)

抓拍传送带上运动的产品时，运动会使图像模糊，导致图像清晰度下降[1]。究其原因是摄像机与目标间产生了相对运动。这种模糊图像给工业生产中的器件计数、识别时图像特征提取带来困难，因此需要对模糊图像恢复才可使后续工作更加准确。

当下模糊图像处理的算法[2-4]很多是基于目标物体与相机的相对运动的，如经典模糊图像处理算法、线性代数复原法(有、无约束最小二乘法)、频域法(如逆滤波、维纳滤波)、非线性代数法(如投影迭代、最大熵复原)、反卷积恢复方法(盲复原法)等。大多数算法是建立已知的退化模型，求出扩散函数PSF(point spread function)。盲复原恢复法是在运动模型未知的情况下对图像进行恢复。它主要是对PSF不断地迭代更新，最终尽可能恢复运动的模糊图像。降质图像恢复效果较好的有维纳滤波法和投影迭代法。基于此，本文以摄像机抓拍传送带上运动的电子元器件的模糊图像为研究对象，比较维纳滤波法和投影迭代法在图像恢复效果上的优劣。

1 系统模型和问题分析

模糊图像的分析，离不开对系统模型的研究，只有准确理解系统的模型，才能更好地实现降质图像的恢复。

1.1 系统模型

如图1所示，当生产线上的电子元器件在摄像机下经过时，其图像被抓捕，采集到的图像交给后台图像处理系统处理。在采集过程中，由于电子元器件与成像系统间存在相对运动，图像就会模糊。生产线传送带运动模型一般可以理解为速度在0.3 m/s至1.0 m/s之间的匀速直线运动。摄像机抓拍图像的时间越短产生的模糊度越小；反之，相对速度愈快、抓拍时间长产生的模糊度就越大。一般情况下，虽然它们的相对运动速度较小，产生的模糊度较小，但是仍给后续的图像处理工作造成误差。

图1 图像采集示意图

1.2 问题分析

图1所示的图像采集系统中，摄像头是不可以转动的，即运动模糊图像产生是因为场景中有运动的物体，这种情形可称为运动物体场景模糊。如图2所示，相机与运动的物体间的相对运动让图像有了拉长(偏移量)的趋势。偏移量是导致图像模糊的直接原因。

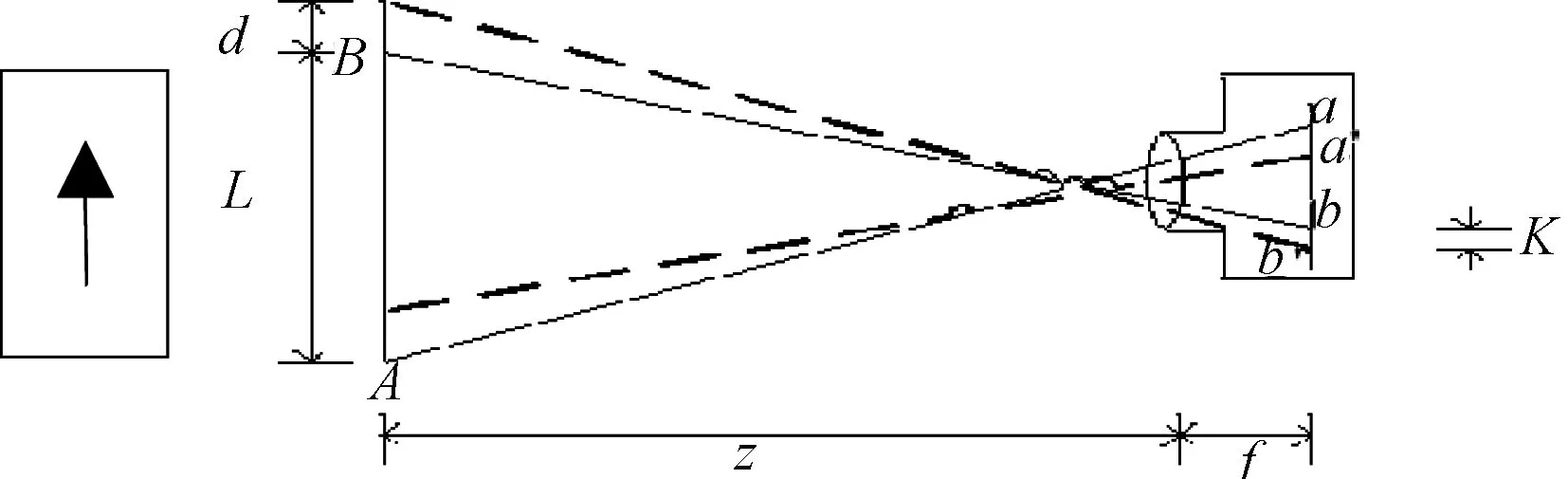
图2 图像退化的成像原理示意图

图3是传输速度为0.5 m/s的传送带上电子元器件的模糊图像，为运动场景的模糊图像。因为传送带传输速度不快，图像模糊程度不算太严重，同时考虑到生产线上退化模型相对简单，所以为使后续图像处理的准确度更高，一般采用频域法和非线性代数法。

(a)

(b)

2 解决方案和逆滤波算法

处理模糊图像一般有2种方式。 1)缩小曝光时间。照相机的曝光时间不可能无限制的减小，因此这种方法的使用受到了限制。2)建立运动图像复原模型。本文通过建立数学模型来解决图像的复原问题，这种方案也是目前工程实例中主要解决方法。

2.1 模糊图像的一般退化模型

降质的一个因素是随机噪声。噪声信号复杂，因此实际上只考虑白噪声(频谱密度为常数)，且在噪声不相关的基础上得出运动模糊退化模型[5-9]。将退化过程用一个模型来表示，即原图像Q(A,B)通过系统H后，与噪声N(A,B)相加得到退化的图像P(A,B)。退化过程示意图如图4所示。

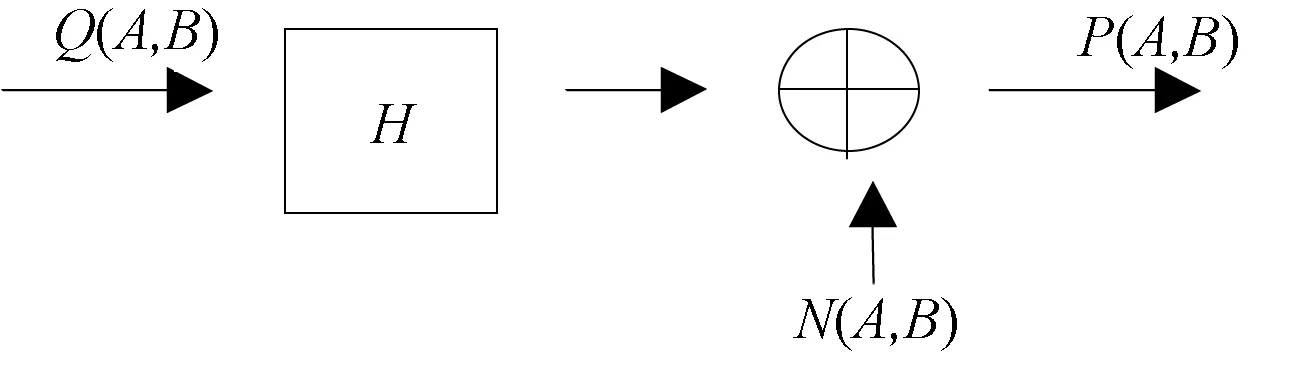
图4 降质模型

由图4模型得出图像降质公式

(1)

假设H是线性不变性系统,产生的退化图像P(A,B)可表示为

P(A,B)=h(x,y)*Q(A,B)+N(A,B)

(2)

该公式可理解为一个退化函数h(x,y)和原图像Q(A,B)卷积后再和噪声N(A,B)求和，生成退化的图像P(A,B)。

式(3)是频域的乘积。如果噪声忽略不计，式(3)可简化为式(4)。

P(u,v)=H(u,v)Q(u,v)+N(u,v)

(3)

P(u,v)=H(u,v)Q(u,v)

(4)

2.2 匀速直线运动退化模型

生产线传送带可以理解为匀速的直线运动。在摄像机抓拍图像瞬间，由于摄像头与传送带有相对运动，产生了运动模糊图像。模糊图像P1(A,t)可表示为实际图像Q1(A,t)的积分

(5)

如果传送带的速度为零，Q1(A,t)=Q(A,B),式(5)就可理解为Q(A)与曝光时间的乘积，只影响成像的反差；但在实际的情况中传送带是运动的，Q1(A,t)与时间的积分就会使得图像变得模糊起来，并且时间越长，模糊程度就愈大，即把Q1(A,t)变为Q(A,B-vt)。匀速直线运动模糊成像关系可表示为

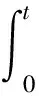
(6)

可以看出，运动模糊图像是由拍摄目标在不同的时间点叠加而形成的。

拍摄目标与摄像机镜头的相对运动的方向和速率影响着匀速直线运动退化模型的确定。

假设图像Q(A,B)是一个二维运动目标，a0(t)和b0(t)分别是在水平和垂直方向变化的分量，T表示运动时间,模糊图像P(A,B)可表示为

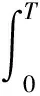
(7)

生产线模型可以简化为水平方向匀速直线运动，故式(7)简化为式(8)。若图像在时间T内的位移量为m,，则运动速率a0(t)=mt/T。式(9)是对它求频域的变换，即匀速直线运动模糊退化模型。

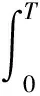
(8)

(9)

由于本文中的运动速率和方向已知，水平方向为匀速直线运动，所以可以考虑用模糊图像的频域下的黑带条纹的个数来确定。对这2个参数的确定就是估计PSF过程。

2.3 逆滤波算法

逆滤波法也称为去卷积算法。它是直接将退化过程H逆变换与降质图像反卷积。模糊图像是原图像经过H系统后加噪声而得到，如图4所示。逆滤波在对其结果进行反卷积，利用傅里叶变换转到频域，如图5所示。

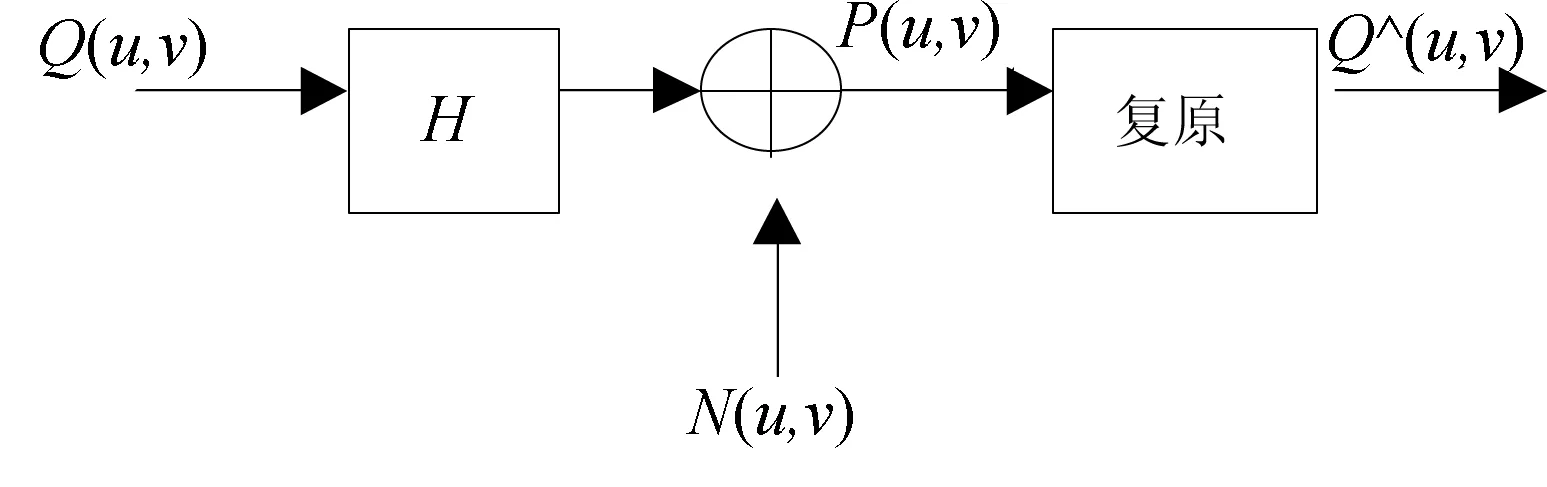
图5 逆滤波的恢复模型

考虑噪声情况下，由式(3)知，Q^(u,v)就是恢复后图像的傅里叶频域变换。P(u,v)表示输入的频域变换；N(u,v)是噪声函数的频域变换；H(u,v)是退化的扩散函数。为克服H(u,v)为零的情况，在分母加上K，Q^(u,v)改为

(10)

逆滤波算法对无噪声污染的图像恢复很有效，但是对有噪声的污染图像，对噪声有放大作用，处理的图像可能比未处理的图像还要模糊，同时往往还会伴有振铃效果。实际应用中噪声常常是无法估算的，因此逆滤波只适合无噪声的恢复。

3 维纳滤波法与投影迭代法

维纳滤波法(最小均方误差)在恢复模糊图像领域应用广泛。投影迭代法是一种非线性算法，把图像描述成了多维空间的一个向量，对模糊图像不断投影迭代得出清晰图像。

3.1 维纳滤波法

维纳滤波最先应用于一维信号的领域且取得了很好的效果，后来这种算法引入到二维信号，也取得了很好的滤波效果[7]。维纳滤波法是以原图像Q(A,B)与恢复后图像Q^(A,B)的均方误差最小为准则，即

E2=min{[Q(A,B)-Q^(A,B)]2}

(11)

满足条件的转移函数如式(12)所示。Sq(u,v)和Sn(u,v)分别表示原图Q(A,B)和噪声N(A,B)的功率频谱密度。

(12)

λ=1是维纳滤波器表达式，此时式(11)取得最小值。Sq(u,v)和Sn(u,v)在未知的情况下用K值表示它们的比值，得出维纳滤波器的表示为

(13)

3.2 投影迭代算法

在忽略噪声的情形下，由式(2)除去N(A,B)后写为矩阵形式可得下面的表达式：

(14)

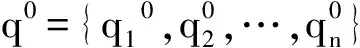
(15)

其中，h1=(h11,h12，…,h1n)。

类似于式(15)，q1对q2进行估计运算，取q1在P2上的投影，表示为h21q1+h22q2+h23q3+…+h2mqm=P2。以此类推最后得出qm，这样就实现了迭代的第1次循环。下一步再取qm投影到第1个平面，直到最后1个方程式，实现第2次循环。假设大小为m×n的图像,按上述方法便可求出q0，qm,q2m，…，它们收敛于q。

4 算法恢复效果比较

本文选取的是速度为0.5 m/s、底色为白色的电子元器件传输带，抓拍传送输带上的运动产品的图像，摄像头静止不动。实验对抓取的模糊图像分别用维纳滤波法和投影迭代法在VC++2008进行恢复仿真。对图3中生产线上2模糊运动图像分别用维纳滤波k=0.1进行处理，得到图6。为保证实时性，对不同的生产线传送带速度和实际的电子元器件的间隔选不同的迭代次数；因此，本文投影迭代法取迭代次数为30进行处理，得到图7。

(a)

(b)

(a)

(b)

下面进行图像的清晰度评价。由文献[10]知，边缘能量越大，图像清晰度越高。本文选取恢复前尺寸大小一样的图像，采用Laplacian模板[9]求出边缘能量的大小。式(16)为Laplacian函数计算公式，计算结果见表1。

(16)

表1 2种算法的清晰度和恢复时间

由表1可知，在实验图片来自于背景颜色单一且轻微模糊和适度噪声的情况下，投影迭代法的清晰度比维纳滤波算法的清晰度高，投影迭代法的恢复效果更好。

5 实时性分析

在投影迭代算法中，选择一个初始值带入式(14)计算出q1，即计算出第1个平面上的投影，以此类推，总共计算m次，完成1次循环。由于图像模糊长度不大，本文循环次数取为3，故投影迭代法的时间复杂度公式为T(m)=O(f(m3))。在传送带传送速度为0.5 m/s的情况下，当计算机CPU单核主频为1.8 GHz，图像尺寸为512×512时, 处理时间在1 s左右；当CPU主频提升2.5GHz和图像尺寸缩小为256×256时，处理时间在0.4 s以内。可以看出，投影迭代算法完全满足实时性要求。

6 结论

生产线上产品图像模糊是影响产品监控和计数等方面的一个关键问题。本文采用维纳滤波法和投影迭代法对生产线上的模糊图像进行处理，并从实时性和清晰度方面对恢复效果的优劣进行比较。仿真结果表明，投影迭代法对生产线上运动产品抓拍产生的轻微模糊图像的恢复效果比维纳滤波方法更优。

[1]Wang wei,Zheng jin-jin,,Liu Xing, et al.Adaptive Detection Method of Degraded Parameters in Motion Blur Image[C]// Fuzzy Systems and Knowledge Discovery.Shanghai:IEEE,2011:2158-2162.

[2]Helstrom C W.Image Restoration by the Method of Least Squres[J].Joural of the Optical Society of America,1967,57(3),273-303.

[3]Yang Y,Galatsanos Np,Stank H. Projection-based Blined Deconvolution[J].Joural of the Optical Society of America A,1994,11(9): 2401-2409.

[4]Babacan S, Molina R, Katsaggelos A. Parameter Estimation in TV Image Restoration using Variational Distribution Approximation[J].IEEE Transaction on Image Processing, 2008,17(3):326-339.

[5]徐飞，施晓红 .Matlab应用图像处理[M].西安：西安电子科技大学出版社, 2002:150-200.

[6]张变莲.一种基于Hough变换的运动模糊图像复原方法[J].科学技术与工程, 2010，10(28)：7018-7021.

[7]明文华,孔晓东,屈磊,等.运动模糊图像的恢复方法研究[J]. 计算机工程,2004,30(7):133-135.

[8]吴振宇.模糊图像复原方法研究[D]. 长沙：国防科学技术大学, 2009.

[9]Li Hui, Fu Chengyu . An Improved Focusing Algorithm based on Image Definition Evaluation[C]// 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce.Deng Leng:IEEE,2011:3743-3746.

[10]Yi Li, Guanzhong Liu . Digital Images Clarity Quality Evaluation Using Non-subsampled ContourletTransform[C]//Computational Intelligence and Design. Changsha:IEEE,2009:318-321.