内置式PV-Trombe墙自然通风的数值研究

徐小炜，苏亚欣

(东华大学 环境学院，上海 201620)

内置式PV-Trombe墙自然通风的数值研究

徐小炜，苏亚欣

(东华大学 环境学院，上海 201620)

提出了一种新的内置式PV-Trombe墙模型，并通过CFD方法对自然通风进行了数值模拟。分析了太阳辐射和流道宽度对气流模式和通风量的影响。结果表明，太阳辐射、流道宽度和高度对通风量的影响非常明显。通风量随太阳辐射强度和高度的增加而增大。当流道宽度从0.1 m增加到0.4 m时，通风量呈单调递增趋势，然而当宽度增加到0.5 m时，流道顶部区域的空气出现回流并且通风量开始减小。对于3 m高的模型，最大通风量出现在流道宽度等于0.4 m时。流道宽度是影响流道内空气自然对流的流动形态的主要因素，当流道宽度尺寸在0.1～0.4 m之间时，流道内的空气为层流热分层流动。当宽度超过0.5 m后，流道上部区域出现的回流使得热分层流动消失，空气从层流向湍流转变。

自然通风；内置式PV-Trombe墙；CFD模拟

太阳能烟囱是一种利用自然通风原理实现建筑的暖通空调的被动式太阳能利用技术[1]。Trombe墙是一种典型的太阳能烟囱，作为一种高效节能的被动式太阳能系统，通常被应用于新建和现有建筑的南墙外立面。典型的Trombe墙结构由朝南方向的集热墙以及一个覆盖在集热墙外面并与之保持一定间距的玻璃盖板构成。太阳辐射穿过玻璃盖板被集热墙吸收并储存，被加热后的墙体则通过自然对流换热的方式加热流道内的空气，驱动空气向上流动，形成自然通风。通过控制Trombe墙上、下的阀门的出口方向达到通风、供暖以及冷却的目的。目前，研究人员对Trombe内墙空气的通风、传热特性及随太阳辐射瞬时变化的动态响应特性等进行了大量的理论与实验研究[2-6]。

光伏建筑一体化Trombe墙(PV-Trombe墙)将光伏电池与Trombe墙相结合，能同时产生热能和电能。季杰等[7-9]提出了一种将光伏电池贴于传统Trombe墙玻璃盖板内侧的PV-TTrombe墙结构，并利用传热理论建立了其能量平衡的数学模型，得到了有关空气以及墙、玻璃等的温度分布等规律[7-8]。虽然该PV-Trombe墙能同时提供热能和电能，但是随着光伏电池在玻璃盖板上的覆盖率的增加，Trombe墙的热效率减小，最大减小17%。当玻璃盖板被光伏电池全部覆盖后，即使考虑光电转换效率，该PV-Trombe墙对太阳能利用的总效率仍然会降低5%[10]。数值模拟结果也表明[11]，当玻璃盖板贴上光伏电池后，Trombe墙流道内以及室内的空气温度都会降低，而这将会减弱系统的供热或通风效果。其原因是光伏电池阻挡了太阳光进入流道内，减少了集热墙的得热量，从而削弱了了流道内的自然通风。

为进一步提高对太阳能的综合利用率，本文提出了一种新的内置式PV-Trombe墙，它将光伏电池贴在Trombe墙的集热墙表面，太阳辐射完全穿过玻璃盖板进入Trombe墙内，并被集热墙表面的太阳能电池吸收，一部分太阳辐射发电，其余部分则用于加热通道内的空气。本文采用计算流体力学(CFD)方法研究该内置式PV-Trombe墙内部的空气流动与通风特性。

1 数值模拟计算说明

1.1 内置式PV-Trombe墙的模型

内置式PV-Trombe墙的物理模型和简化模型如图1所示。该物理模型主要包括外部的玻璃盖板，铺设在集热墙表面的光伏电池面板；电池与墙面之间以绝热材料相隔，玻璃盖板与光伏面板之间构成一个带开口的空气流道。太阳辐射能透过玻璃被电池吸收，其中一小部分转化成电能，剩下的绝大部分转化成热能，使电池的温度升高。流道内的空气与电池表面进行自然对流换热，空气受热后便产生自下而上的流动，形成自然通风。流动的空气带走电池表面热量、冷却电池表面，电池的温度降低，使电池发电效率得到提高。

在简化模型中，玻璃和光伏面板两侧受太阳辐射S所获得的恒定热流密度分别用q1和q2表示，流道的高度和宽度用H和b表示，两者的变化范围分别为1～6 m和0.1～0.6 m。空气流经模型底部的水平进口进入空气流道并由竖直出口流出，开口大小与Trombe墙空气流道的宽度相等。并假设模型底部黑色粗线标识部分为绝热墙体。

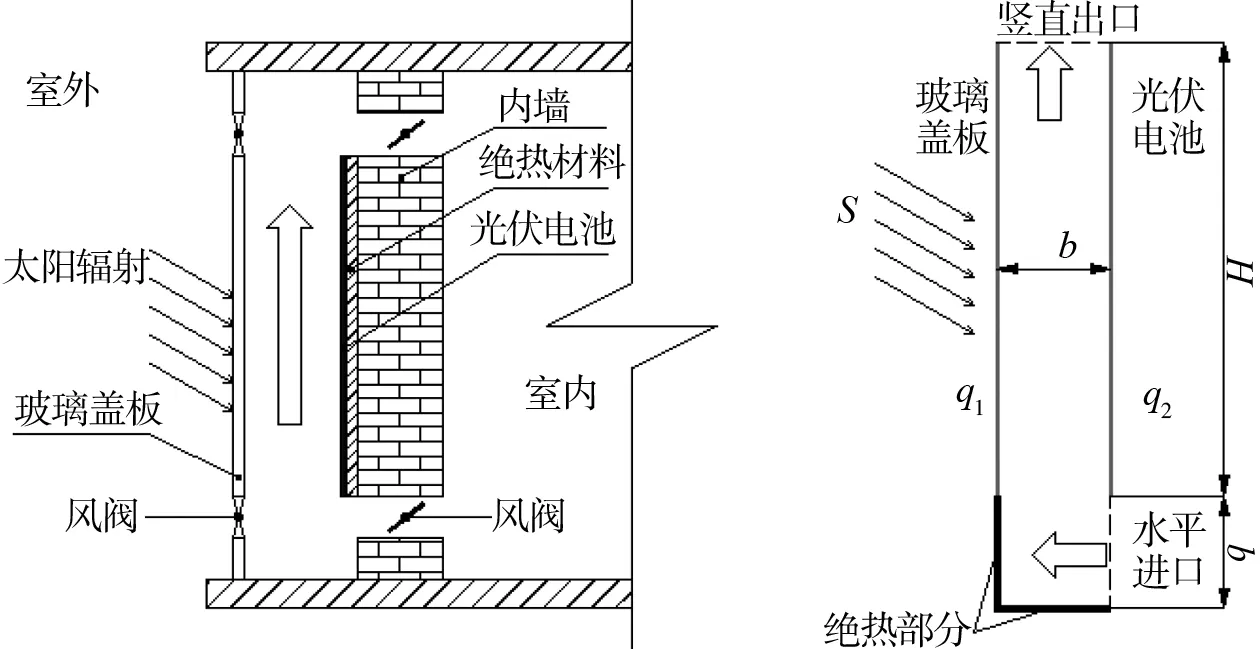
图1 内置式PV-Trombe墙的物理模型及简化模型

1.2 数值模型

Gan[12]对典型的Trombe墙内自然通风的CFD模拟表明，采用RNG κ-ε湍流模型的计算结果与实验数据基本吻合。因此采用能较好的处理低雷诺数和近壁流动问题的RNG κ-ε模型模拟流道内空气的的流动和传热情况。Boussinesq假设用于处理动量方程中因温差而引起的浮力项的改变。基于以上假设，对于二维稳态、不可压缩的浮力驱动流，其流动和传热的通用控制方程可写为：

式中：Φ代表xi方向上的平均速度vi、湍流参数或者是平均温度；ΓΦ表示扩散系数，SΦ为变量Φ的源项。

离散坐标辐射(DO)模型用于计算玻璃与光伏电池之间的辐射换热。考虑到近壁面处温度梯度和速度梯度变化较大，壁面附近选用增强壁面函数法进行处理。在计算过程中不断细化网格，最终得到计算结果与网格无关的网格尺寸。本文模拟中，模型的水平进口和竖直出口设为压力进口和压力出口；玻璃盖板和光伏电池表面的热流密度恒定，具体数值需结合太阳辐射强度大小经计算确定。采用二阶迎风格式对方程进行离散，用SIMPLE法进行求解，采用Fluent 6.3[13]完成计算。

2 数值计算结果与分析

2.1 模拟方法的可靠性验证

Gan[5]运用CFD方法对二维通风腔内空气流动特点进行模拟计算。运用本文模拟方法计算Gan[5]所研究的竖直通风腔，并将流道内空气体积流量的计算结果与Gan[5]中的相关数据作对比来确认本文模拟方法的可靠性，对比结果如图2和图3所示。从图中可以明显看出，本文模拟结果与原文数据基本一致，证明了本文模拟方法的可靠性并可以用于对内置式PV-Trombe墙通风性能的进一步研究。

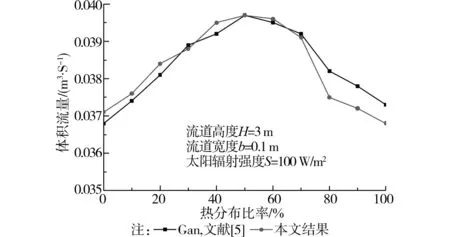
图2 b=0.1 m时流道内空气体积流量对比结果

图3 b=0.3 m时流道内空气体积流量对比结果

2.2 太阳辐射对流道内气流的影响

内置式PV-Trombe墙内部的空气流动是影响流道内光伏电池表面传热系数和通风量大小的关键因素。空气流动受到包括太阳辐射强度、流道高度和宽度等参数的影响。太阳辐射是使空气受热并产生向上流动的能量来源。流道被空气的压力分布、流速矢量分布以及自然通风的空气体积流量的计算结果如图4～7所示。

当内置式PV-Trombe墙的几何尺寸相同时，随着太阳辐射强度的增加，太阳能电池吸收了更多的太阳辐射后，流经太阳能电池表面的空气通过自然对流换热也得到更多的热量，因此，其上升的速度将增加，从而引起了内部压力的降低，如图4所示。对比在同一高度上的压力分布发现，随着太阳辐射强度的增加，沿Trombe墙的相同高度上空气的负压的绝对值增大，这表明，通道内空气的流速增加了，即太阳辐射强度使得Trombe墙内的自然通风增强。图4中所示的压力等值线的水平分布特点表明，当H=3 m,b=0.3 m时，Trombe墙内的空气呈热分层流动。

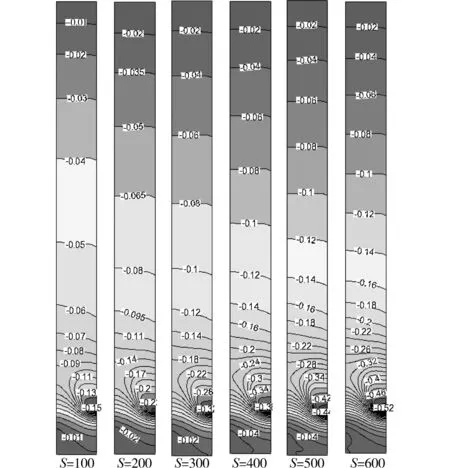
图4 流道内压力场分布图(Pa)(H=3 m,b=0.3 m，图中太阳辐射强度S的单位为W/m2)

图5 流道内速度矢量分布图(H=3 m,b=0.3 m，图中太阳辐射强度S的单位为W/m2 )

从图5中所示的速度矢量图中可以看出，在空气进口处都会产生局部的涡流区。在右侧墙体表面的光伏电池吸收太阳辐射能并加热空气，因此空气沿着PV面板形成自然对流边界层，该边界层未出现局部旋涡，为层流。图6为在Trombe墙内高度为1.5 m处的局部空气速度沿流道宽度方向的分布，它表明在Trombe墙内右侧墙体表面附近的空气速度最大，且流道内的空气速度随太阳辐射强度的增加而增大。空气流速的增加必然使得Trombe墙的通风量增加。图7表示通风量随着太阳辐射强度的变化规律。通风量的定义为流道截面面积和出口处平均速度的乘积。结果表明随着太阳辐射的增强，通风量随之增加。

图6 截面高度为1.5 m处的速度沿宽度方向的分布图

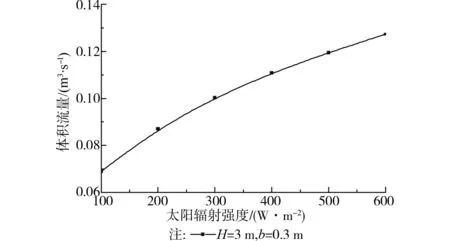
图7 空气体积流量随太阳辐射的变化曲线

2.3 流道宽度对流道内气流的影响

前人的研究表明，Trombe墙的流道宽度是影响Trombe墙自然通风量的主要因素之一[12，14]。Gan[12]通过CFD方法模拟一个传统的Trombe墙的自然通风特性时发现，对于开口大小等于流道宽度的Trombe墙，当流道宽度在0.05～0.4 m之间时，空气流量随流道宽度的增大而持续增加。Burek和Habeb[14]通过实验对传统的Trombe墙内的空气流动特性的研究结果也表明当流道宽度在0.02～0.12 m范围内变化时，空气流量也表现出类似分布规律。为深入分析流道宽度的影响，作者对高度H=3 m和太阳辐射强度S=400 W/m2时，流道宽度对内置式PV-Trombe墙的流动特性的影响进行了计算，结果如图8～11所示。

图8 宽度不同时流道内压力场分布 (Pa)(H=3 m，S=400 W/m2，图中宽度b的单位为m)

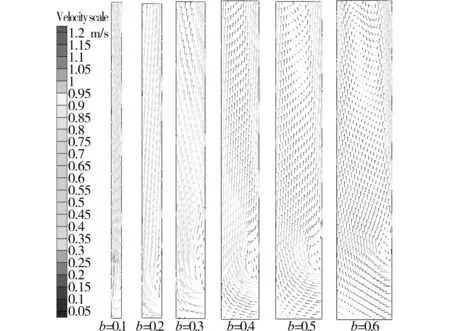
图9 宽度不同时流道内速度矢量分布图(H=3 m，S=400 W/m2，图中宽度b的单位为m)

图8表明，随着流道宽度的增加，内置式PV-Trombe墙流道内在相同高度上的负压等压线的绝对值逐渐减小，表明空气受热上升的速度有所减小。当太阳辐射强度一定时，被吸热墙表面的太阳能电池吸收的热量一定，而随着流道宽度的增加，流经电池表面的空气质量增多，因而空气被加热后温度升高的幅度减弱，使得其因热浮力而产生的上升运动减弱。当流道宽度小于0.4 m时，等压线 呈水平分布，表明流道内的空气保持热分层流动特点。图9的速度矢量分布表明，随着流道宽度的增加，流道内空气向上运动的速度减小。在右侧电池表面形成的自然对流边界层中未出现旋涡，因此其流动为层流。随着流道宽度的继续增加，如当b超过0.5 m后，流道内的等压线变为曲线，如图8所示，而图9的速度矢量图则表明在流道上部出现了回流旋涡，流道内的气流也不再是热分层流动，流动模式发生改变。

自然对流流动的流态可以用Gr数来表征。对于均匀受热壁面，定义下面的Gr数[15]：

当太阳辐射S=400 W/m2，烟囱高度H=3 m时，由式(2)计算出不同宽度时的Gr数，如表1所示。

表1 不同宽度时的Gr数

单侧竖直热壁面表面发生自然对流时，当式(2)定义的Gr数的大小为104～3×109时，流动为层流；当Gr数的大小为3×109～2×1010时，流动处于过渡区；当Gr数>2×1010后流动为湍流[15]。由表1的不同宽度时Gr数的大小可知，随着宽度的增加，烟囱内的空气流动逐渐从层流向湍流转化，因而出现了局部旋涡。

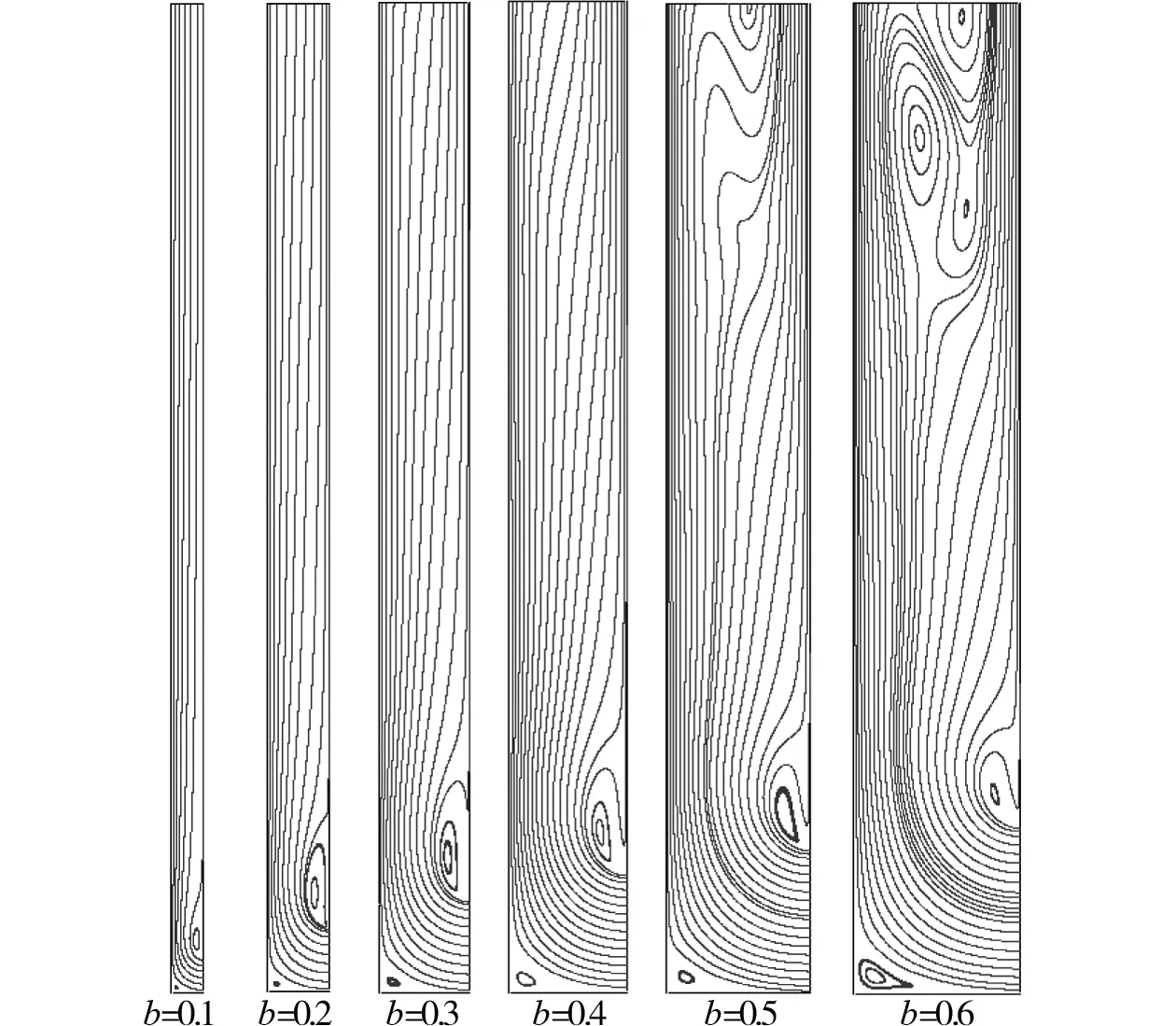
图10 不同宽度时流道内空气流线图(H=3 m，S=400 W/m2，图中宽度b的单位为m)

图11 空气体积流量随宽度的变化曲线(H=3 m)

图10给出了流道内空气流动的流线，清楚了表明了随着宽度的增加，空气流动方式逐渐从层流向湍流转变。回流的产生会增加额外的空气流动阻力，因此流道的通风量也受到影响。图11为通风量随流道宽度的变化曲线。当宽度从0.2 m增加到0.4 m时，通风量呈递增趋势。而当宽度超过0.5 m之后，通风量随之下降。

2.4 高度对流道内气流的影响

图12 S=400 W/m2，b=0.3 m时等压线分布(单位：Pa，其中高度H变化范围为1～6 m)

内置式PV-Trombe墙的高度对流道内气流的影响如图12～13所示。当S=400 W/m2，b=0.3 m时，流道内的等压线随着高度的增加依然保持水平，而没有出现弯曲，如图12所示。这说明随着高度的增加，流道内并没有出现涡流，空气依然保持了热分层流动。从等压线的绝对值的变化特点来看，随着高度的增加，流道内的负压的绝对值增大，表明空气向上流动的速度增加了。图13的速度矢量图更加清楚地表明了这一变化特点。这是由于高度增加后，空气在上升的沿程中吸收了更多的太阳辐射，其浮力增加，因而上升的速度增大。由于流道内未形成局部涡流，因而其流动本质上是层流。当空气速度随Trombe墙的高度增加而增大时，通风量也必然增大，结果如图14所示。因此，内置式PV-Trombe墙的高度不影响流道内的空气的流态，而流道宽度则是影响通道内空气流态的主要参数。

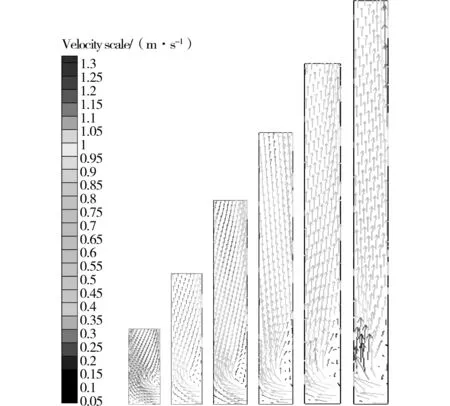
图13 S=400 W/m2，b=0.3 m时速度矢量分布(单位：m/s，其中高度H变化范围为1～6 m)

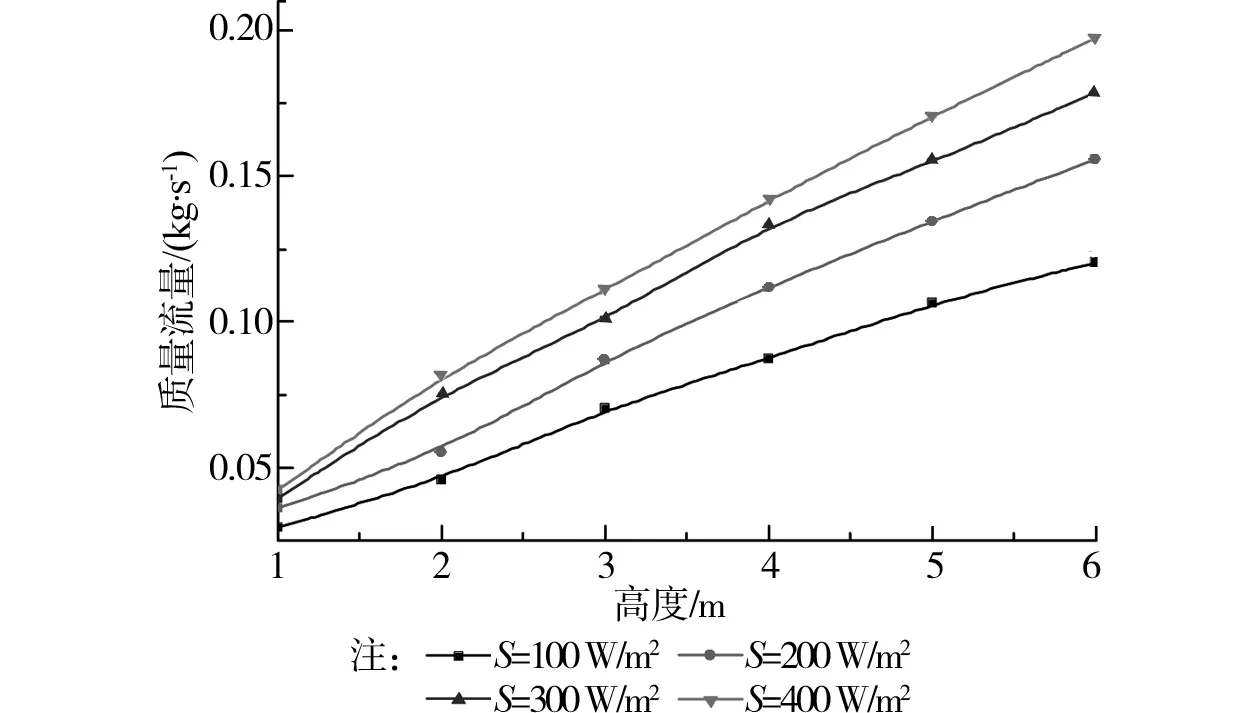
图14 高度对通风量的影响(b= 0.3 m)

3 结 论

提出了一种以同时实现自然通风和发电新的内置式PV-Trombe墙，并采用CFD方法对流道内空气流动进行了数值模拟，分析了太阳辐射、流道宽度、高度对空气流动模式和通风量的影响。从本文的研究结果可以得出以下结论：

1)内置式PV-Trombe墙的随太阳辐射的增强而增大。随着太阳辐射强度的增加，通道内空气的流速增加，通风量增大。当H=3 m,b=0.3 m时，Trombe墙内的空气呈热分层流动。

2)流道宽度是影响流道内空气自然对流的流动形态的主要因素。当流道宽度尺寸在0.1～0.4 m之间时，流道内的空气为层流热分层流动，通风量随宽度的增加而增大。而当宽度超过0.5 m后，流道上部区域出现回流，空气从层流向湍流转变，热分层流动消失，通风量随宽度的增加而减小。当模型高度H=3 m而宽度为0.4 m时，流道内空气的体积流量达到最大值。

3)内置式PV-Trombe墙的高度不影响流道内的空气的流态，随着高度的增加，流道内的空气向上流动的速度增加，从而通风量增大。不同高度时空气依然保持热分层流动。

[1] 苏亚欣，柳仲宝.太阳能烟囱强化自然通风的研究现状[J].科技导报,2011,29(27):67-72.

Su Y X, Liu Z B, Research status on solar chimney for natural ventilation enhancement [J]. Sclence Review and Technology, 2011, 29(27):67-72.

[2] Saadatian O, Sopian K, Lim C H, et al. Trombe walls: A review of opportunities and challenges in research and development [J]. Renewable and Sustainable Energy Reviews, 2012, 16(8): 6340-6351.

[3] Bansal N K, Mathur J, Mathur S, et al. Modeling of window-sized solar chimneys for ventilation [J]. Building and Environment, 2005, 40(10): 1302-1308.

[4] Ong K S, Chow C C. Performance of a solar chimney[J]. Solar Energy, 2003, 74(1): 1-17.

[5] Gan G. Simulation of buoyancy-driven natural ventilation of buildings-Impact of computational domain [J]. Energy and Buildings, 2010, 42(18): 1290-1300.

[6] Zamora B, Kaiser A S. Optimum wall-to-wall spacing in solar chimney shaped channels in natural convection by numerical investigation[J]. Applied Thermal Engineering, 2009, 29(4): 762-769.

[7] Ji J, Yi H, He W, et al. Modeling of a novel Trombe wall with PV cells [J]. Building and Environment, 2007, 42(3): 1544-1552.

[8] Ji J, Yi H, Pei G, et al. Study of PV-Trombe wall installed in a fenestrated room with heat storage[J]. Applied Thermal Engineering, 2007, 27(8): 1507-1515.

[9] 季杰，蒋斌,陆剑平，等.新型PV-Trombe墙的实验[J].中国科学技术大学学报，2006，36(4):349-354.

Ji J, Jiang B, Lu J P, et al. Experimental study on a movel PV-Trombe wall [J]. Jourmal of University of Science and Technology of China, 2006,36(4):349-354.

[10] Sun W, Ji J, Luo C, et al. Performance of PV-Trombe wall in winter correlated with south facade design [J]. Applied Energy, 2011, 88(1):224-231.

[11] Koyunbaba B K, Yilmaz Z. The comparison of Trombe wall systems with single glass, double glass and PV panels [J]. Renewable Energy, 2012, 45:111-118.

[12] Gan G. A parameter study of Trombe walls for passive cooling of buildings [J]. Energy and Building, 1998, 27(1):37-43.

[13] FLUENT user’s guide [M]. New Hampshire, USA: Fluent Inc; 2006.

[14] Burek S A M, Habeb A. Air flow and thermal efficiency characteristics in solar chimneys and Trombe Walls [J]. Energy and Buildings, 2007, 39(2):128-135.

[15] 杨世铭，陶文铨. 传热学[M]. 北京：高等教育出版社，1998.

(编辑 胡 玲)

NumericalanalysisofNaturalVentilationinBuilt-inPhotovoltaic-TrombeWall

XuXiaowei,SuYaxin

(School of Environmental Science and Engineering, Donghua University,Shanghai 201620, P.R.China)

The natural ventilation in a novel built-in photovoltaic-Trombe wall (BiPV-TW) was numerically simulated by CFD method. The effect of solar radiation, channel width and height on the air flow pattern and ventilation rate was analyzed. Results show that the solar radiation, channel width and height influenced the ventilation rate remarkably. As the solar radiation and BiPV-TW height increased,the ventilation rate increased. As the channel width increasing from 0.1 m to 0.4 m, the ventilation rate monotonously increased. However, when the channel width exceeded 0.5 m, the reverse flow was formed in the top zone and the ventilation rate decreased. A maximum air volume flow rate was achieved when the channel width was approximately equal to 0.4 m in a 3 m height model. The channel width was the dominant factor that influenced the flow pattern in the channel. When the channel width was smaller than 0.4 m, the airflow was thermally stratified laminar flow. When the channel width exceeded 0.5 m, thermally stratified flow disappeared due to the reverse flow formed in the top zone and the laminar flow became turbulent.

natural ventilation; built-in photovoltaic-Trombe wall; CFD simulation

10.11835/j.issn.1674-4764.2014.05.004

2014-01-18

国家自然科学基金(51278095)

徐小炜(1988-)，男，主要从事建筑节能及新能源与建筑一体化研究，(E-mail)xuxiaowei0118@foxmail.com。 苏亚欣(通信作者)，男，教授，博士,(E-mail)suyx@dhu.edu.cn。

TK 519

A

1674-4764(2014)05-0023-06