桩筏基础与地基共同作用的半解析半数值分析法
2014-09-04朱李春陈水胜冯震华吕国敏苏天凤雷泽临
朱李春,陈水胜,冯震华,吕国敏,苏天凤,雷泽临
(中国水产科学研究院 南海水产研究所,农业部南海渔业资源环境科学观测实验站,广州 510300)
桩筏基础与地基共同作用的半解析半数值分析法
朱李春,陈水胜,冯震华,吕国敏,苏天凤,雷泽临
(中国水产科学研究院 南海水产研究所,农业部南海渔业资源环境科学观测实验站,广州 510300)
将群桩筏板基础离散成桩和弹性板,桩筏基础与地基的共同作用转化为桩、弹性板与地基之间的力与位移协调分析。对不同的地基模型求解相应的地基柔度系数,同时将桩作为弹性杆件求解其柔度系数,并将筏板视为地基上的四边自由矩形板,求出其在地基反力、桩顶反力和外荷载以及简支边广义位移共同作用下的位移,最后通过力和位移协调建立桩、筏、地基之间的共同作用方程并求解。算例对比表明半解析半数值方法具有较好的精度,能满足实际工程计算需要。
桩筏基础;共同作用;半解析半数值法
地基基础共同作用计算目前采用的方法主要是数值方法和解析方法,数值方法一般是采用有限单元法,而解析方法主要包括边界元法和半解析方法。考虑到地基的半无限性,有限单元法[1]在计算时单元多,计算时间长,难于模拟无限域,难以在实际工程计算采用,半解析半数值法[2]和边界元法[3]由于直接采用地基的解析解,因此地基无需作大量网格划分,容易满足计算要求。
地基上筏板计算主要有两种考虑方法,一种是将筏板视为刚性板,另一种是将筏板作为地基上的弹性板板,桩的计算也主要有两种不同的处理方式,一种是将桩视为弹性杆件,按压杆计算,另一种是将桩分为若干个单元段,根据桩土之间侧摩阻力的分布规律[4]采取不同的计算模型。倪光乐等[5-6]基于地基上的四边弹性自由板给出了解析解答,在此基础上,蔡健等[7]给出了加勒板与地基共同作用的分析,何春保等[8]曾对有埋深情况下的地基基础共同作用进行了分析对比。这些半解析方法在共同作用计算中都得到了较好的效果。在此基础上,利用板的弹性理论解,以及桩、筏、土之间的相互协调,采用半数值半解析分析方法,来建立考虑筏板实际弹性刚度的桩筏基础共同作用分析方法。并通过实例计算对比来验证本文方法的实用性。
1 共同作用网格划分
如图1所示,地基上的筏板长宽尺寸为a×b,共划分为nn个网格单元(nn=ni×nj),ni、nj为基础在x,y两个方向划分的网格数,i=1,2…ni,j=1,2…nj。
对于有桩的位置,将其看作桩单元,并视桩为弹性杆件,编号为1、2、iz、、nz,如图2所示。这样桩筏基础与地基的共同作用可以转化为筏板、桩、土之间的力与位移协调分析。

图1 筏板基础网格划分

图2 群桩系统
2 地基柔度系数
为了计算地基的变形,需要根据不同的地基模型计算相应的地基柔度系数,目前弹性地基模型主要包括文克尔地基模型和弹性半空间地基模型(Boussinesq解和Mindlin解),相应的地基柔度系数si,j计算如下。
1)文克尔地基模型
2)弹性半空间模型Boussinesq解
集中荷载的Boussinesq位移解为[5]

在i点作用单位力,在j点产生的沉降可以通过积分得到
其中μ为土的泊松比。
3)弹性半空间模型Mindlin解
由于Boussinesq解适用于荷载作用于地表的情况,对于有埋深的基础,竖向集中力作用于半空间内部一点(0,0,+c)时,在半空间任意点(x,y,z)处产生的沉降为(如图3)。

对于均布荷载作用于埋深ζ的面积(ξ2-ξ1)×(η2-η1)上时,通过对式(2)积分,可以得到在点(x,y,0)处产生的沉降为

进一步对式(5)进行积分,可以得到在j网格作用单位力,在i点产生的地基沉降si,j为[8],

其中:

K1、K2为与力作用点和所求点相关的函数,可表示为,

3 桩的柔度系数
桩的沉降计算方法很多,主要跟桩土之间的接触模型有关,不同的接触模型会得到不同的沉降计算表达式,由于桩筏基础中筏板的内力和变形是设计较为关注的,而对于桩,一般主要关注桩顶压力和桩的沉降,采用不同的桩土接触计算模型得到的桩顶压力和沉降计算结果往往差别不大。为了计算简便,桩顶沉降按以下3部分计算[9]:
其中:Sc、Sr、Ss分别为桩身混凝土的压缩、桩底岩石的变形和沉渣的压缩。分别按下式计算。
其中:R为桩顶压力;Rf为桩周的摩擦力,可按相关规范取值计算得到;Rb为桩底压力;A为桩身(桩底)截面积;l为桩长;db为桩身直径;Ec、Er、Es分别为混凝土、桩底岩石和沉渣的变形模量;ω为形状系数;hs为沉渣厚度。对于无沉渣的情况,Sc=0,对于支承于硬质岩石上的桩基Sr=0。
以下为了计算方便,对于第iz条桩,相应的以上各量用下标iz表示,如Riz、Siz分别为第iz条桩的桩顶反力和沉降。
4 弹性矩形板理论解
筏板可以视为四周自由板,其在荷载作用下的位移解可以由文[10]的叠加方法得到,包括以下四部分。
1)在板内(ξ2-ξ1)×(η2-η1)面积上受到局部均布力q作用时四边简支矩形板的解为[5]
其中:



ξ、η、δξ、δη为X作用中心点坐标和长宽尺寸。
2)四边简支矩形板受地基反力作用时的位移解
第j网格单位地基反力X作用下板的位移为
其中
Ajm,n=

其中ξxj、ηxj、δξxj、δηxj为局部均布力q作用中心点坐标和长宽尺寸。
3)四边简支矩形板受桩顶反力作用时的位移解
第iz条桩单位桩顶反力Riz作用下板的位移为

其中
Azm,n=

其中ξziz、ηziz、δξziz、δηziz为桩反力R换算成矩形面积均布荷载后作用中心点坐标和长宽尺寸。
4)四条简支边分别发生广义位移时的位移解为[11]
其中:

合并以上4部分解答得到板的总变形为

5 共同作用方程的建立
桩筏基础系统离散成桩、筏板、地基后,其相互间的共同作用平衡方程包括以下4部分
1)基础板与地基的位移协调

第i网格中心筏板的变形为


由接触网格中心地基沉降与筏板变形相等得到地基与筏板的位移协调方程


2)基础板与桩的位移协调
第iz条桩顶处桩的沉降为Siz
第iz条桩顶处筏板的变形为:
(Δ0+xiztanα0+yiztanβ0)-

由桩的沉降与筏板变形在接触处相等得到桩与筏板的位移协调方程
(Δ0+xiztanα0+yiztanβ0)-

3)基础板静力平衡方程

x方向弯矩平衡:
y方向弯矩平衡:
式中:xi,yi为筏板网格中心坐标;xiz,yiz为桩中心坐标;Δ0,α0,β0分别为基础板的角点刚体位移以及两个方向绕角点的转角;∑FZ,∑Mx,∑My为基础板面所受的外力及两个方向的弯矩;
4)基础板四边自由边界条件方程
地基上的四边自由板必须满足四边剪力为零,按照剪力计算公式有
Vx(x,y)=
地基上的四边自由板由于板面荷载、地基反力、桩顶反力以及板边广义位移等3种情况下而产生的板边剪力分别如下。
1)板面荷载q作用下在y=0、y=b、x=0、x=a边产生的剪力为
2)地基反力X作用下在y=0、y=b、x=0、x=a边产生的剪力为
3)第iz根桩的桩顶反力Riz作用下在y=0、y=b、x=0、x=a边产生的剪力为
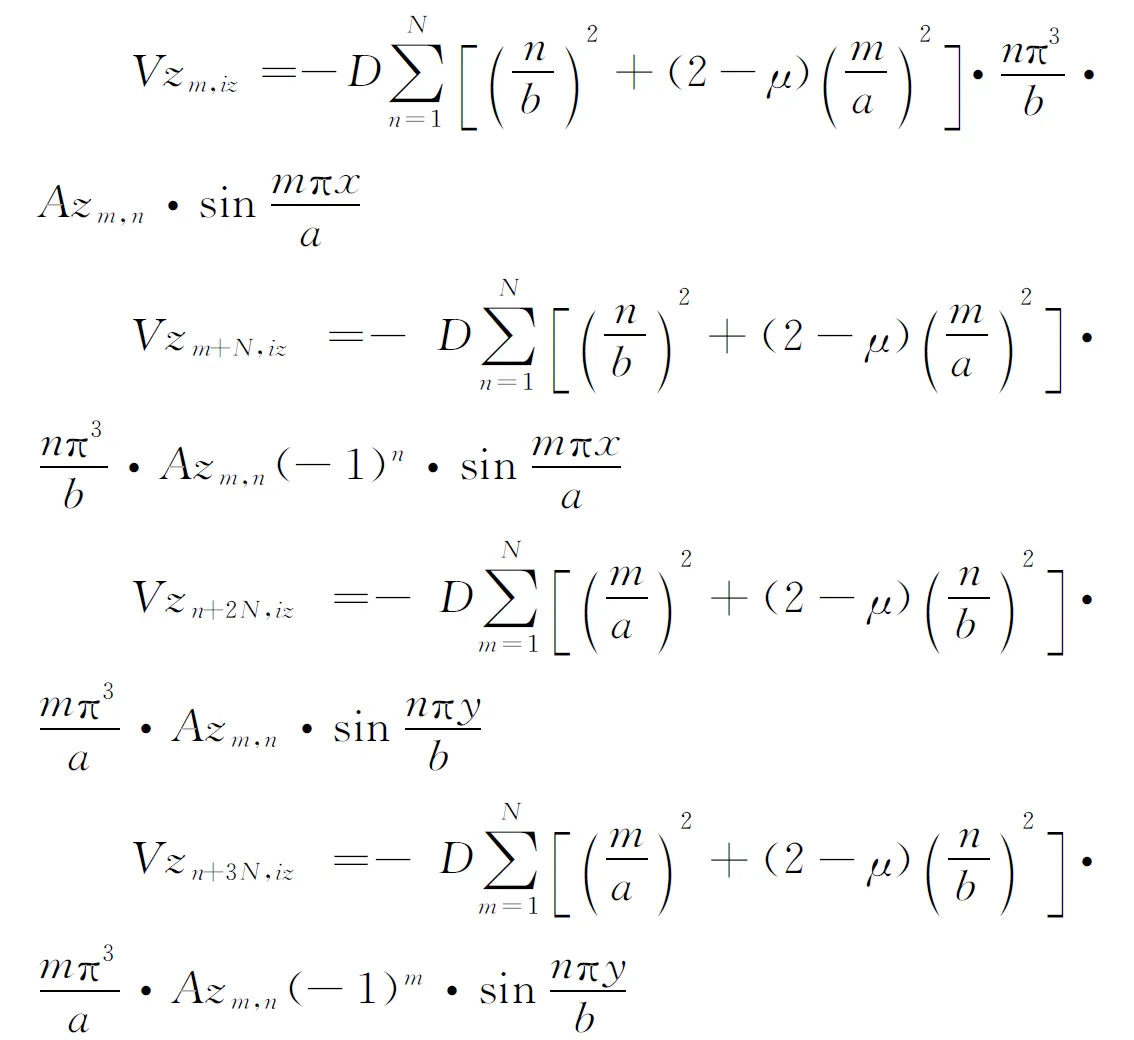
4)由于板边广义位移而在y=0、y=b、x=0、x=a边产生的剪力

筏板必须满足四边剪力为零的边界条件,由以上板面荷载、地基反力、桩顶反力、板边广义位移作用下的剪力公式得到:
其中:

以上方程包含的未知量个数为筏板单元划分数ninj,与地基反力未知数相对应。筏板板的刚体位移Δ0和两个方向的转角α0,β0与筏板的三个方向的力平衡方程相对应。筏板四周剪力为零的方程与其四边的四个广义位移系数λm、λm+N、λn+zN、λn+3N相对应。桩顶与筏板的平衡方程与nz个桩顶反力相对应。合并方程(13)~(18)、(19),方程数和未知量个数相等,从而可以求解桩筏基础与地基的共同作用(当筏板为刚性板时,wi,j=0,Δi,p=0)。
6 算例分析
30层的高层建筑[12]由2块相互分离的桩筏基础支承。每块筏基的平面尺寸均为22 m×17.5 m,厚度为2.5 m。每块独立的筏基下有42根桩,桩径D为900 mm。桩长20 m,总荷载为130 MN。计算采用的力学参数如下:
1)筏板:弹性模量ER=2.85×107kPa,泊松比μR=0.17;2)桩:桩长L=20 m,桩径D=900 mm,弹性模量Ep=2.85×107KPa;3)地基:土的弹性模量按Sommer原文取值,考虑了土体的速度效应,ES=7(1+0.35z) MPa,其中z为深度,泊松比μS=0.50;4)C40混凝土:柱网6.15 m×6.28 m,柱截面0.55 m×0.55 m,上部计算荷载为21层。
桩筏基础的平面布置与单元划分等见图4~图7。将筏板划分为195个单元,共有42个桩单元,153个土单元,共有12个桩荷载,分别作用于17#、21#、25#、29#、92#、96#、100#、104#、167#、171#、175#、179#筏板单元上。

图4 基础单元划分

图5 桩编号

图6 桩编号

图7 地基土层分布
Sommer采用弹塑性有限元法计算得到的结果和本文计算结果以及实测情况对比如表1所示。

表1 计算结果对比
桩荷载比=角桩荷载∶边桩荷载∶中桩荷载
本文模型计算结果与实测结果相比,无论在平均沉降、土承载比例及桩荷载比方面均较接近,这反映本文计算方法的合理性。
本文对弹性板和刚性板平均沉降及地基土荷载承担比例进行了计算,计算结果如图8~9和表2~表3所示。

图8 不同厚度基础板的P-S曲线

图9 地基土承载比例与荷载水平关系

表2 筏板沉降分布 mm

表3 桩顶反力 MN
比较计算结果可以看出,刚性板情况下计算结果与2.5m厚弹性板情况下计算结果相差不大,主要是由于2.5 m厚弹性板刚度已经很大。弹性板方法能较好的计算得到筏板的差异沉降。
7 结 论
基于地基的弹性半空间解和板、杆件的弹性理论,通过桩、筏、土之间的位移协调建立了桩、筏、地基土共同作用半解析半数值方法,工程实例表明本文方法具有较好的精度,克服了有限单元法在计算上难于模拟地基的半无限性以及计算速度较慢的缺点,可以用于桩-弹性板-地基的共同作用计算。
[1] Lee K M, Xiao Z R. A simplified nonlinear approach for pile group settlement analysis in multilayered soils [J]. Canadian Geotechnical Journal, 2001,38 (5) : 1063-1080
[2] Wang Y H,Tham L G,Tsui Y,et al. Plate on layered foundation analyzed by a semi-analytical and semi-numerical method[J]. Computers and Geotechnics,2003,30:409-418.
[3] 尚守平、杜运兴、周芬.桩箱(筏)基础与地基土共同作用的分析研究,土木工程学报,2001,34(4):93-97.
Shang S P, Du Y X, Zhou F. Study on the interaction of subsoil and piled box(raft)foundation [J]. China Civil Engineering Journal,2001,34(4):93-97.
[4] 倪光乐,李成明,苏克之.弹性矩形板与弹性地基共同作用的简化计算法[J].岩石力学与工程学报.2000,19(5):659-665.
Ni G L, Li C M, Su K Z.A simple computational method of interaction between elastic plate and elastic subground [J].Chinese Journal of Rock Mechanics and Engineering.2000,19(5):659-665.
[5] 倪光乐,苏克之,李成明. 弹性矩形板与非线性地基共同作用的简化计算法[J]. 岩土力学,2000,21(3):239-243.
Ni G L,Su K Z,Li C M. A non-linear concentrated spring model and its application[J]. Rock And Soil Mechanics,2003,30:409-418.
[6] 赖琼华. 桩基沉降实用计算方法[J].岩石力学与工程学报,2004,23(6):1015-1019.
Lai Q H. Practical calculation procedure of pile-foundation settlement [J].Chinese Journal of Rock Mechanics and Engineering,2004,23(6):1015-1019.
[7] 蔡健,何春保, 沈建华,等. 梁板式矩形筏基与地基共同作用的弹性分析[J].岩石力学与工程学报,2005,24(10):1804-1810.
Cai J,He C B,Shen J H,et al. Elastic analysis of interaction between stiffened raft and subsoil [J].Chinese Journal of Rock Mechanics and Engineering,2005,24(10):1804-1810.
[8] 何春保,蔡健,倪光乐,等. 深置矩形基础与地基共同作用的解析分析[J].岩土力学,2007 ,28(12):2553-2559.
He C B,Cai J,Ni G L, et al. Analytical analysis of interaction between deep rectangular foundation and groundsill [J]. Rock and Soil Mechanics, 2007, 28(12): 2553-2559.
[9] 陆培炎. 桩基设计方法[J].岩石力学与工程学报,1994,13(4):375-388.
Lu P Y. Design method of pile foundation [J].Chinese Journal of Rock Mechanics and Engineering,1994,13(4):375-388.
[10] 刘鸿文. 板壳理论[M]. 杭州:浙江大学出版社,1987.
[11] 张福范. 弹性薄板[M]. 北京: 科学出版社,1984.
[12] Sommer H,et al. Piled raft foundation of a tall building in Frankfurt Clay[J]. XI Int.Conf.on SMFE,1985,2253-2257.
(编辑 胡 玲)
InteractionBetweenPiles-RaftFoundationandGroundBasedonaSemi-AnalyticalandSemi-NumericalMethod
ZhuLichun,ChenShuisheng,FengZhenhua,LvGuomin,SuTianfeng,LeiZelin
(South China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences; Scientific Observing and Experimental Station of South China Sea Fishery Resources & Environments, Ministry of Agriculture, Guangzhou 510300, P.R.China)
Considering the piles-raft foundation as a composite system of piles and elastic plate, the interaction between piles-raft foundation and soil is translated into the compatible analysis of force and displacement among piles,elastic plate and ground. Based on different models of foundation subjected to centralized load,the settlement coefficient subjected to uniform load is obtained by means of integral, The flexibility coefficient of piles is calculated by considering the pile as elastic member, and with raft identified as four sides free rectangle plate on the ground, the displacement of raft suffering external loads, counter force of soil and generalized displacement on the boundary could be obtained. A semi-analytical and semi-numerical method, using compatible analysis of force and displacement between piles,elastic plate and ground,is developed to analyze the interaction between piles-raft and subsoil. Numerical analysis prove that the semi-analytical and semi-numerical method is provide an accurate and practical calculation tool to. and meet the needs of practical engineering.
piled raft foundation; interaction; semi-analytical and semi-numerical method
10.11835/j.issn.1674-4764.2014.05.017
2014-01-21
国家科技支撑计划课题(2012BAD18B02、2012BAD18B01-2);国家公益性行业(农业)科研专项(201003068)
朱李春(1987-),男,主要从事岩土工程研究,(E-mail)zlcktt1987@126.com。 陈水胜(通信作者),男,副研究员,(E-mail)chsslt8@163.com。
TU473
A
1674-4764(2014)05-0103-08
