PTFE针刺非织造过滤材料蠕变模型的建立与验证*
2014-09-03
(东华大学纺织学院,上海,201620)
随着我国综合实力的提升,以电力、建材、冶金、化工等能源消耗性为主的重工业发展迅速;此外,随着我国城市化进程的加快,城市规模的扩大,人口数量的增加,使城市生活垃圾量呈高速递增趋势,垃圾焚烧处理工程也应运而起。上述高污染、高耗能产业的发展,在促进社会和经济发展的同时,也带来了严峻的环境污染问题,主要表现为烟尘类颗粒物、高温烟气、有毒气体等大气污染物的排放[1]。
工业上粉尘过滤的方法有电除尘、湿法除尘和袋式除尘等,其中袋式除尘法占较大比重,袋式除尘器需要配备过滤材料[2]。聚四氟乙烯(PTFE)材料在高温下强度保持率高,水解稳定性能好,阻燃性好,可耐强氧化物及各种酸碱的腐蚀,过滤效率高,清灰性能良好[3]。PTFE过滤材料在应用于脉冲清灰滤袋中时,由于长时间受到高过滤风速及脉冲力的作用,必须具有两个主要的性能,即能在长时期的工作过程中保持其强力和只发生很小的蠕变。但PTFE抗蠕变性能差,因此有必要研究其蠕变性能以及蠕变过程的模型化,并判断长期工作环境下的蠕变量是否影响其工作的稳定性。
1 试验部分
1.1 材料及仪器
试样的常温蠕变试验在土工布合成材料蠕变试验仪上进行,试验仪如图1所示。

图1 土工合成材料蠕变试验仪示意
该试验仪夹持试样的上下夹具距离可根据需要调节,本试验的夹具距离设定为100 mm;试验采用的砝码有5、10和20 kg三种,可以任意组合,以满足试验中各级荷载要求;用高精确度的电子数显指示表测量试样的蠕变量,有效地减少了由于人工测量读数带来的误差。
本试验的试样是纯PTFE的带基布的针刺非织造过滤材料。由PTFE长纤维编织基布,用PTFE短纤维在基布表面经加工制成针刺毡。针刺毡面密度700 g/m2,耐温260 ℃,纵向断裂强力900 N/(5 cm),横向断裂强力700 N/(5 cm),过滤效率99.8%。
本试验采取20%、40%、60%和80%断裂强力的四级荷载,相对应的荷载依次为180、360、540和720 N,等效单宽荷载为180 N/cm,研究了试样在四级不同断裂荷载下的蠕变行为。
1.2 试验数据
本试验于2012年9月10日开始,将试样固定在蠕变试验仪上,静置24 h后对各试样分别加载,至本文撰写完毕时已经持续试验超过了1 000 h,试验仍在继续中。
试样尺寸50 mm×100 mm,试验环境温度20 ℃,相对湿度60%。试验500 h内的部分数据见表1。

表1 常温蠕变量 (单位:mm)
由表1可知:在承受60%及以上极限荷载时,试样的应变变化率比低荷载水平作用下的应变变化率大,即在较短的时间内就发生相当明显的变形,并快速出现断裂。这说明PTFE针刺过滤材料不宜在60%及以上极限荷载的高荷载情况下应用;试验的蠕变特性与承受荷载大小有密切的关系,荷载越大,其应变越大,应变速率也越大。
2 PTFE针刺非织造过滤材料蠕变模型的建立
目前国内还没有关于PTFE针刺非织造过滤材料蠕变模型的相关报道,但是分别描述PTFE纤维和非织造土工布蠕变模型,以及相关理论的研究报道有很多。陈碧波[4]建立了适合填充PTFE的压缩蠕变模型,李艳琴[5]研究了适合两布一膜土工布的蠕变模型——六元件并联模型和六元件串联模型。本课题参照两布一膜土工布的蠕变模型,与本文作者提出的假设进行了对比分析,并通过origin软件对模型的可行性进行了验证。
2.1 六元件串联模型
加基布的针刺非织造过滤材料的结构可看作是两层纤网夹一层织物,两层纤网可看作是两个并联的开尔文模型,中间基布可看作是一黏性体,故设计出五元件模型[6],见图2。

图2 五元件模型
因为两层纤网的受力相同,故两开尔文模型中的弹簧杨氏模量E和牛顿黏壶的黏滞系数η相同。
根据串联原理,各部分应力σ相同,应变ε为各部分的和:
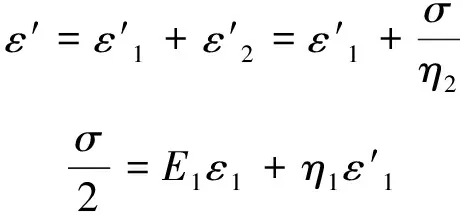
联立上式,消去ε1,得到该模型的本构方程式:
(1)
当在恒定应力作用下,即σ=σc=常数,公式(1)变换为:

根据初始条件:t=0,ε(0)=0
解微分方程,可得:
(2)
公式(2)是五元件模型模拟针刺过滤材料蠕变性能的蠕变应变公式。从公式(2)可以看出,该模型缺少瞬时变形,故与实际不符。因此,可猜想应在该模型中串联一虎克弹簧,构成六元件模型,如图3。

图3 六元件串联模型
六元件模型的总应变是在五元件模型应变的基础上加上弹簧的应变,故模型的总应变量为:
(3)
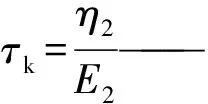
2.2 六元件并联模型
谢莉青等[7]用光杠杆法测试非织造土工布的蠕变性能,得到了用线性简易三元件力学模型能较好地模拟非织造土工布蠕变性能的结论。针刺加筋过滤材料是两层纤网间复合PTFE长丝基布,其强力和抗蠕变性能明显优于非织造材料。简化针刺加筋过滤材料结构模型时,是把基布看作为一层非织造材料,即是两层非织造布复合在一起。若用三元件来模拟单一的非织造布,则针刺加筋过滤材料可以看作是由两个三元件模型并联在一起,在本文中是两个开尔文标准线性固体模型相并联,如图4所示。
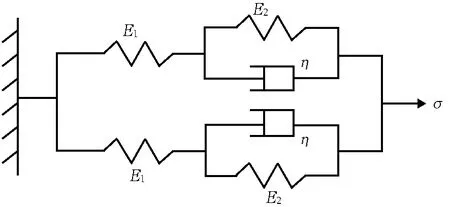
图4 六元件并联模型
假设图4中的两个开尔文标准性固体模型中虎克弹簧的杨氏模量和牛顿黏壶的黏滞系数相同,根据串并联原理,模型的总应力为两个开尔文标准线性固体模型的应力之和,即:
结构的总应变与每个开尔文标准线性固体模型的总应变相等,即:
上式对时间t求导,得:
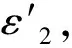
(4)
蠕变时应力为常数,即σ=σc,则σ′=0。
模型的本构关系式变为:
首先使σc=0,上式可化简为:
解之得:
从本构方程中看出特解为:
则有:

(5)
公式(5)就是六元件并联模型的蠕变应变公式。
3 利用origin软件验证模型的可行性
可以对上述六元件并联及串联模型的蠕变应变公式进行简单的变形,然后在origin软件的内置函数中找出与其应变公式相对应的函数,用此函数对500 h内的试验数据进行拟合。拟合精度高,说明此模型可行;反之,拟合精度低,说明模型不适合描述该试样的蠕变行为。
3.1 利用origin软件验证六元件并联模型的可行性
对六元件并联模型蠕变应变公式[公式(5)]进行变换。
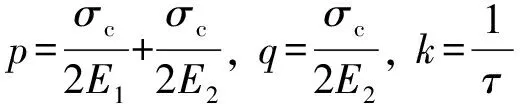
则:ε=p+qe-kt
令:y=ε,x=t
则:y=p+qe-kx
(1)把试样在20%荷载下的蠕变数据根据origin中的内置函数Yidfert1进行拟合,拟合曲线见图5。
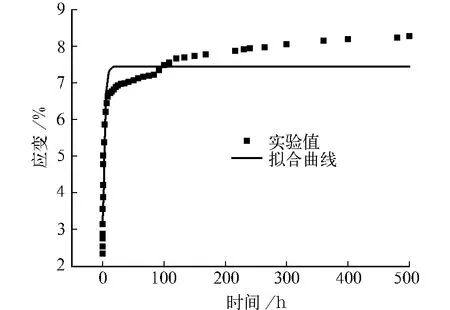
图5 六元件并联模型对20%荷载试样的拟合曲线
20%荷载试样的拟合公式为:
y=7.450 1-4.386e-0.338 3x
相关系数R2=0.914 44
因为相关系数R2大于0.85,故该拟合有效。
把常数p、q、k还原为E1、E2和η,即:
20%荷载试样的应变公式为:
(6)
(2)把试样在40%荷载下的蠕变数据根据origin中的内置函数Yidfert1进行拟合,拟合曲线见图6。
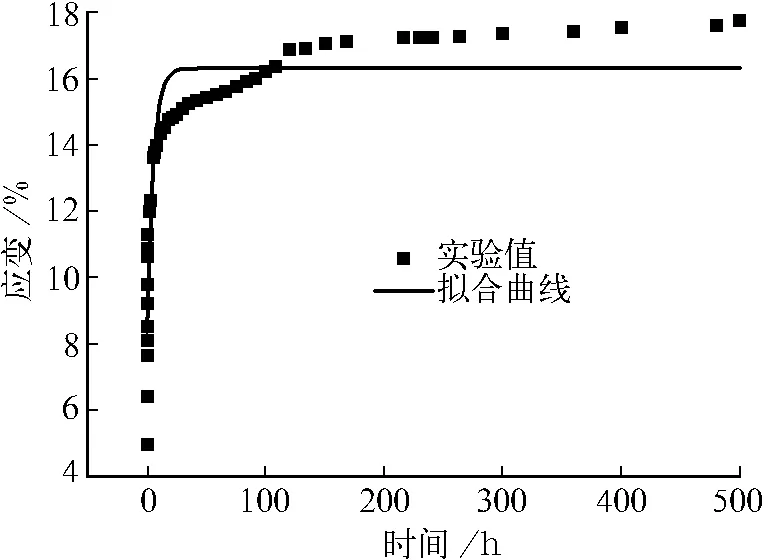
图6 六元件并联模型对40%荷载试样的拟合曲线
40%荷载试样的拟合公式为:
y=16.329-7.988e-0.190 6x
相关系数R2=0.882 44
因为相关系数R2大于0.85,故该拟合有效。
把常数p、q、k还原为E1、E2和η,即:
40%荷载试样的应变公式为:
(7)
对比公式(6)和公式(7)可以看到,E1、E2的计算值很接近,而由于试验误差等原因,η值的差距较大,但仍然能够推测试样在20%及40%荷载下的蠕变行为可以用六元件并联模型来表示。
3.2 利用origin软件验证六元件串联模型的可行性
对六元件串联模型蠕变应变公式[公式(3)]进行变换:
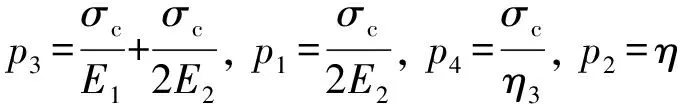
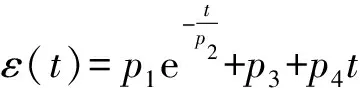
令:y=ε(t),x=k
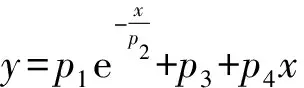
(1)把试样在20%荷载下的蠕变数据根据origin中的内置函数ExpLinear进行拟合,拟合曲线见图7。
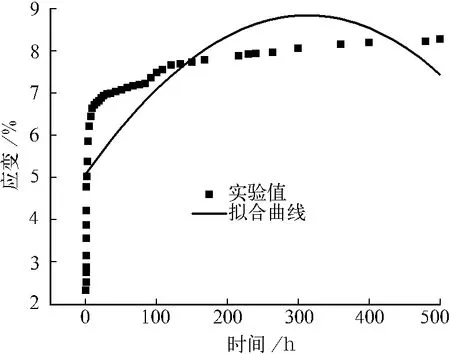
图7 六元件串联模型对20%荷载试样的拟合曲线
20%荷载试样的拟合公式为:
相关系数R2=0.541 28
因为相关系数R2小于0.85,故该拟合无效,说明六元件串联模型不适合用来描述在20%荷载下试样的蠕变规律。
(2)把试样在40%荷载下的蠕变数据根据origin中的内置函数ExpLinear进行拟合,拟合曲线见图8。
40%荷载试样的拟合公式为:
相关系数R2=0.371 52
因为相关系数R2小于0.85,故该拟合无效,说明六元件串联模型不适合用来描述在40%荷载下试样的蠕变规律。
由图7和图8可以看出,六元件串联结构对模拟PTFE针刺非织造过滤材料的蠕变行为是不成功的,不适合用来描述该材料的蠕变规律。

图8 六元件串联模型对40%荷载试样的拟合曲线
4 结论
本文在高分子材料蠕变行为的理论基础上,借鉴以往对PTFE纤维及非织造土工布蠕变性能的研究结论,提出了六元件并联模型及六元件串联模型,并利用origin软件对两种蠕变模型进行了拟合。结果证明:六元件并联模型可以很好地模拟PTFE针刺非织造过滤材料的蠕变行为,并给出了常数数值,确定了模型的公式;而六元件串联模型对模拟PTFE针刺非织造过滤材料的蠕变行为是失败的,不适合用来描述该材料的蠕变规律。
[1] 朱平,宋尚军.高温过滤材料的现状与发展趋势[J].玻璃纤维,2010(6):34-38.
[2] 中国环保产业协会袋式除尘委员会.袋式除尘器过滤材料及配件手册[M].沈阳:东北大学出版社,2007:5-11.
[3] 邱新标.聚四氟乙烯纤维复合针刺毡过滤材料的研发与应用[J].非织造布,2009,17(6):17-21.
[4] 陈碧波.聚四氟乙烯蠕变性能研究[D].西安:西北工业大学,2007.
[5] 李艳琴.复合土工布蠕变性能的研究[D].青岛:山东大学,2006.
[6] 于伟东,储才元.纺织物理[M].上海:中国纺织大学出版社,2001:79-80.
[7] 谢莉青,张洪弟.用光杠杆法测试分析非织造土工布的蠕变性能[J].产业用纺织品,2001,19(2):32-34.
