具有有界控制输入的不确定时滞系统的渐近稳定性*
2014-09-03陈衍峰
陈衍峰
(通化师范学院 数学学院,吉林 通化 134002)
具有有界控制输入的不确定时滞系统的渐近稳定性*
陈衍峰
(通化师范学院 数学学院,吉林 通化 134002)
针对控制输入满足某个有界约束的不确定时滞系统,其中的不确定性满足范数有界不确定性,提出了无记忆饱和全局渐近稳定的控制律的设计方法,数值算例说明了所给方法的有效性.
时滞系统;控制约束;范数有界不确定性
在控制系统的分析与综合中,一般假定控制输入不受任何约束.即控制输入可以取任何有限值.然而,对于众多的实际工程控制系统来说,所有的执行机构都或多或少的存在某种程度的物理约束.而且在对实际工程系统进行控制时,还必须将有界的控制输入对闭环系统性能的影响,尤其是对闭环系统稳定性的影响考虑进去.目前实际控制系统的控制约束一般分为两类.一类是研究当控制输入有界时,其闭环系统的控制特性下降较大,应该如何设计控制系统的控制器以使得闭环系统稳定;另一类是设计控制系统保证在有界控制输入下控制系统为全局渐近稳定的.前者需要开环系统满足在有界输入下为渐近零可控制的性质,而后者需要采用适当的方法,估计闭环系统的稳定区域.
本文利用李雅普诺夫稳定性定理和苏尔补引理,同时结合饱和函数的上确界,给出闭环系统是全局渐近稳定的方法.
1 问题描述
考虑时滞不确定系统
(1)
其中:x(t)为状态向量;d是时滞;A0和B为已知适当维数的常数矩阵;A1是已知的可逆矩阵;u(t)为输入向量,且满足下面的约束条件.
u(t)∈Ω=[-Δ,+Δ],Δ>0
(2)
ΔA是不确定矩阵,且满足下面的范数有界形式
ΔA=DFE1
(3)
其中,D和E1是已知适当维数的确定矩阵,F是未知矩阵,且满足FTF≤I.
本文的目的是,对不确定时滞系统(1)设计无记忆饱和控制器
u(k)=satΔ(Kx(t))=
sign(Kx(t))min{Δ,|Kx(t)|}
(4)
使其闭环系统渐近稳定.
根据上面所述,则对给定的矩阵D、E1和对称正定矩阵P1,存在对称正定矩阵P0,使得下式成立
P0(A0+BK)+(A0+BK)TP0=
(5)
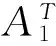
定义一个开椭球体
Ω(P0,r)={x∈Rn|xTP0x (6) 和饱和函数μ,则对一切x∈Rn有u(t)=satΔ(Kx(t))=(1-μ)Kx(t).因此,系统(1)的闭环系统为 [A0+(1-μ)BK+ΔA]x(t)+A1x(k-d) (7) 定理1 如果系统(1)满足条件4,则 (1)当λmin(E)≥-1,系统(1)的闭环系统(7)全局渐近稳定; (2)当λmin(E)<-1,系统(1)的闭环系统(7)局部渐近稳定. 证明 取lyapunov函数 于是,V(x(t))沿闭环系统式(7)有 xT(t-d)P1x(t-d)=xT(t)NTP0x(t)+ xT(t)P0A1x(t-d)+xT(t)P1x(t)- xT(t-d)P1x(t-d)=xT(t)[(A0+BK)TP0+ P0(A0+BK)+ΔATP0+P0ΔA-μE+P1]x(t)+ xT(t-d)P1x(t-d)≤xT(t)[(A0+BK)TP0+ P0(A0+BK)+P0DDTP0+ETE-μE+P1]x(t)+ xT(t-d)P1x(t-d) 其中,N=A0+(1-μ)BK+ΔA.将(5)代入上式有 考虑不确定时滞系统 从而又可以求得 因此,根据定理1知系统(1)的闭环系统是局部渐近稳定的. [1]常青,周立群.具时滞细胞神经网络周期解的全局渐近稳定性[J].天津师范大学学报,2012,32(4):22-31. [2]F.Blanchini.SetInvarianceinControl[J].Automatica,1999,35(11):1747-1769. [3]俞立,徐建明.具有控制约束的不确定离散系统最优保性能控制[J].系统工程与电子,2004,26(10):1453-1456. [4]王永强.输入受约束系统的稳定性分析及抗饱和控制研究[D].杭州:浙江大学,2006. [5]张桂香,金翅,叶振凯.具有有界控制输入的状态反馈控制系统闭环稳定性[J].计算技术与自动化,2002,21(2):16-19. (责任编辑:王宏志) Asymptotic Stability of Uncertain Time-delay System with Bounded Control Constrain CHEN Yan-feng (CollegeofMathematics,TonghuaNormalUniversity,Tonghua,Jilin134002,China) Asymptotic stabilization problem of uncertain time-delay system with bounded control constrain is studied. The uncertainty satisfying norm-bounded is assumed. The explicit design method of memoryless saturated control law for global asymptotic stability is presented. The effectiveness of the approach is shown with examples. time-delay system; control constrain; norm-bounded uncertainty 2013-12-10 陈衍峰(1977-),男,吉林梅河口人,硕士,讲师. 吉林省教育厅“十二五”科学技术研究项目(吉教科合字[2012]第524号). O231 A 1008-7974(2014)01-0017-02
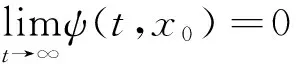
2 控制器设计
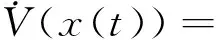
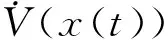
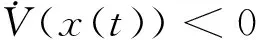
3 数值算例


