滑模控制方法在电机转速控制中的应用
2014-09-02王伟光
王伟光
(哈尔滨电气动力装备有限公司,黑龙江 哈尔滨 150040)
滑模控制方法在电机转速控制中的应用
王伟光
(哈尔滨电气动力装备有限公司,黑龙江 哈尔滨 150040)
滑模控制方法属于非线性控制方法中的一种,现以永磁同步电机为对象,提出采用滑模控制方法对其进行转速控制,并验证控制效果。
电机;转速控制;滑模控制技术
1 永磁同步电机控制技术
电机控制技术的发展是建立在电力电子器件微处理芯片技术发展的基础之上的。在当前集成电路技术发展迅速的背景下,新一代电力电子集成器件能够将功率放大器、电机电流保护电路集成在一起,从而为开发精度控制能力更高、可靠性更强的电机控制系统提供了便利;而微处理芯片技术的进步则直接决定了先进的控制算法的实际应用,在微处理技术较为落后的时候,高性能的控制算法只能进行理论研究,而缺乏实现的工具[1]。近年来,随着微处理技术的快速发展,出现了许多高性能的微处理器,运算能力大大增强,从而为精度更高、控制能力更强的控制算法的应用提供了可能。
对电机进行控制,说到底是控制电机在某一时刻的实际转速与期望转速一致,或者转子的位置与期望的位置一致,因此,为了有效地控制电机的转速或转子的位置,必须获取电机转子的位置和速度信息,从而可以根据当前电机转子的位置或速度与期望值之间的差距进行控制。为了获取电机转子的位置或速度信息,需要采用诸如光电传感器等元器件获取电机转子的位置或速度信息,在大多数电机控制系统中,常采用光电传感器进行信息测量工作,光电传感器具有抗干扰能力相对较强、精度高等优点。然而,传感器的引入增加了电机控制系统的复杂性,因此,不少研究人员提出了采用无位置传感器的控制技术[2-3],例如使用滑模观测器或者采用人工智能领域新进展的神经网络进行辨识,获取位置、速度信息。
此外,当前工程应用领域中常采用矢量控制或直接转矩控制来实现对电机的高精度转速动态过程控制。矢量控制是由SIEMENS提出的基于磁场定向的控制方法,该方法通过矢量平移变换将电机的交流电变换为2个互相垂直的分量,可以分别对2个电流进行控制,从而实现对电机转速的高性能动态控制。目前,矢量控制方法在电机高性能动态控制中应用范围较为广泛。而直接转矩控制方法则直接计算磁链和转矩,利用离散点PWM信号控制逆变器开关,从而直接实现了转矩控制。该方法应用于电机控制系统中,能够使系统更加简化,但同时也有其不足之处,即控制信号有较大变化时,会引起磁链和电机转矩发生较大波动,不利于电机的稳定运行[4]。
除此之外,国内外学者针对电机控制提出了其他大量的方法,例如应用领域十分广泛的比例—积分—微分控制(PID控制)。PID控制具有实现方式简单、应用范围广泛、参数易于调节等特点,在大多数控制领域都能发挥有效的控制效果。然而,电机本身是一个具有十分复杂耦合结构的非线性系统,因此单独的PID控制方法并不能十分有效地实现电机高性能控制。为此,不少研究人员探索了将自适应控制方式、模糊控制、人工智能控制方式引入电机控制中。本文将要介绍的滑模控制方法就是一种能够有效实现对非线性系统的控制的方式。
2 滑模控制技术Equation Section (Next)
滑模控制又称变结构控制、滑模变结构控制,该方法首先由前苏联学者提出,后经其他研究人员的不断丰富、扩展,现已成为非线性控制领域应用十分广泛的控制方法。在针对非线性控制对象进行滑模控制设计的时候,首先应根据对象期望的动态特性设计滑模面,当系统的运动状态达到滑模面上之后,就能够沿着滑模面运动到稳定点,因此,设计好滑模面之后,如果能够控制系统的状态点达到滑模面,或者有限次穿过滑模面之后停留在滑模面上,就能够使系统的状态沿着滑模面达到平衡点。因此,采用滑模变结构控制技术控制非线性对象包括2个步骤:首先设计系统切换函数,即滑模面,处于该滑模面上的运动状态都能够达到系统的平衡点;其次,设计滑模控制律,使系统的状态能够由初始状态运动到滑模面上,并沿着滑模面达到系统的平衡点。滑模控制律设计完成之后,系统就能沿着滑模面达到平衡点,因此,滑模面的设计好坏在很大程度上影响着系统的动态性能。常用的滑模面主要有线性和非线性之分,最常用的线性滑模面的形式如式(1)所示:
S=Cx
(1)
式中,x为系统的运动状态;C为滑模系数。
调整好滑模系数之后,就能够使滑模面上的运动点沿着期望的动态性能运行到平衡点,常用的调整滑模系数的方法有李雅普诺夫方法和微分几何方法等。由于普通线性滑模面的设计较为简单,参数调整也较容易,因此其应用范围较为广泛。但是该方法也有其局限性,在面对结构较为复杂的非线性系统时,其控制效果也相对有限。
为了适应更加复杂的非线性控制对象,国内外研究人员研究了Terminal滑模、积分滑模等方法,以Terminal滑模为例,该方法虽然滑模面比线性滑模复杂,但是具有收敛速度更快、抗干扰能力更强、稳定精度更高等优良特点,式(2)给出了Terminal滑模面:
(2)
在式(2)中,要求参数p和q为奇数,且p>q>0,当系统通过滑模控制律的控制到达滑模面之后,将在有限时间内沿着滑模面达到平衡点,并且该有限时间为:
(3)
从式(3)可以看出,通过设计参数β、p和q,就可以实现对滑模面的设计以及达到时间的控制。
此外,应用较为广泛的还有积分滑模控制方法,与Terminal滑模类似,积分滑模的滑模面如式(4)所示:
(4)
类似于线性控制方法中的PID控制,kp和kl分别为比例、积分系数。同样,适当调整这2个系数就可以有效地实现滑模面的设计,从而实现期望的动态性能。
3 滑模控制在电机转速控制中的应用
下面以永磁同步电机为例,采用积分滑模控制的方法设计滑模控制器,实现对电机转速的有效控制,使电机的速度能够与期望的运转速度保持一致。假设期望的电机运行速度为w0,且该期望函数具有连续的二阶倒数,电机的实际运行速度为w,则电机的转速误差量为:
ew=w0-w
(5)
对式(5)求导并代入电机运动方程得:
(6)
设计如下的二阶积分滑模面:
(7)
对于速度误差跟踪控制系统,有:
iq=ieq+isw
(8)
式(8)中的λ1、λ2、γ1和γ2各参数值均为正,采用Liyapunov定理即可证明该二阶积分滑模能够使系统收敛于稳定状态。对于本文的研究对象来说,将滑模面设计为二阶积分滑模面,能够通过调节参数k1、k2、λ1、λ2实现控制精度的调整,并且通过有效地调整参数γ1和γ2,改善系统的收敛速度。本文采用Simulink工具箱建立了电机控制系统模型[5],并设计控制参数k1=1、k2=14、λ1=50、λ2=1 200、γ1=1 500、γ2=3 000,仿真验证表明,该二阶滑模能够有效地控制电机转速。图1为采用滑模控制方法控制下电机在阶跃信号作用下转速随时间变化的曲线。
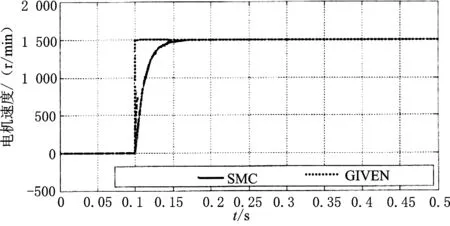
图1 二阶滑模控制电机转速变化曲线
由图1可以看出,采用二阶滑模控制方式,电机在阶跃信号作用下,具有较快的响应速度,并且控制效果较好,转速误差控制在较小的范围内(10-3数量级)。并且系统的控制信号抖震现象得到了有效的抑制,使电机不至于忽快忽慢,造成电机硬件损伤。
4 结语
本文首先阐述了电机转速控制的常用方法,包括矢量控制、直接转矩控制、PID控制等算法,并指出了其不足之处。然后简要介绍了滑模控制方法,包括线性滑模面和以Terminal滑模面、积分滑模为代表的非线性滑模面的设计方法,并以积分滑模为例,设计了二阶滑模控制器,采用仿真验证的方法,验证了本文所提的滑模控制方法在电机转速控制中的有效性。
[1] 蒋继云.永磁同步电机控制[J].科技视界,2012(17):182~183
[2] 梁艳,李永东.无传感器永磁同步电机矢量控制系统概述[J].电气传动,2003(4):4~9
[3] 尚喆,赵荣祥,窦汝振.基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J].中国电机工程学报,2007(3):23~27
[4] 贾洪平,孙丹,贺益康.基于滑模变结构的永磁同步电机直接转矩控制[J].中国电机工程学报,2006(20):134~138
[5] 李三东,薛花,纪志成.基于Matlab永磁同步电机控制系统的仿真建模[J].江南大学学报:自然科学版,2004(2):115~120
2014-09-11
王伟光(1981—),男,吉林公主岭人,工程师,研究方向:电机电磁场分析及拖动控制。
