谱负MAP波动理论的一个注记
2014-09-01张超权唐胜达秦永松
张超权*,唐胜达,秦永松
(1.桂林航天工业学院信息工程系,中国 桂林 541004;2.广西师范大学数学科学学院,中国 桂林 541004)
谱负MAP波动理论的一个注记
张超权1*,唐胜达2,秦永松2
(1.桂林航天工业学院信息工程系,中国 桂林 541004;2.广西师范大学数学科学学院,中国 桂林 541004)
谱负MAP是应用概率论领域的重要内容之一.利用Asmussen-kella鞅推广了谱负MAP(X,J)的波动理论,给出谱负MAP在与之独立且服从Erlang分布的随机时刻点上水平与极值的联合变换所满足的等式,进而由Erlangization方法,给出谱负MAP(X,J)的水平与极值的联合变换的瞬时趋近算法.
谱负MAP;波动理论;Erlangization方法;趋近计算式
Levy过程是应用概率领域内的重要随机过程之一,但是Levy过程的平稳性使其在实际应用中受到一定的局限性.在实际建模中,过程会因长时间的演变、外界随机因素的干扰等原因而不再具有平稳性,如价格的季节性,行为的模式化等.由此,可将Levy过程推广为机制转换模型(regime-switching model):连续时间的Markov加过程(Markov additive process),简称MAP,这是Levy过程的一个自然推广,MAP已成为随机复杂系统的重要建模工具之一,它已被广泛应用于网络通讯、存储论、交通管理、风险过程、金融工程等领域[1-2].
许多学者对MAP的相关性质作了深入的研究,Cinlar,Ney,Asmussen[3-5]给出了MAP的基本结构及性质,Ivanovs[6]给出了MAP的指数矩阵特征值的性质,D’Auria等[7]给出了MAP首达时过程的转移率矩阵的结构,并将其应用于单边反射MAP及双边MMBM[8],Breuer[9]给出了首达时过程的转移率矩阵的迭代计算方法,Ivanovs[10]给出了MAP的scale 矩阵,Kypianou等[11]对MAP波动理论进行了研究.
Avram[12]在研究风险过程中得出破产时刻的Laplace变换等价于指数随机时间内的破产概率,Asmussen等[13]采用fluid embedding方法将这一结果推广并得出服从Erlang(n,q)分布的随机时刻内的破产概率,当给定分布期望不变时,随着分布的阶数趋于无穷,这一随机时刻趋于它的期望定值,利用这一方法,Asmussen等得到了在有限时刻内破产的趋近算法,且这一算法具有良好的稳定性且收敛速度快,这一方法称为Erlangization方法;Stanford[14]将这一方法推广为PH分布情形;Ramaswami等[15]将这一方法应用于随机流体理论,用于各种有限时刻内的各种首达时的研究,Woolford等[16]将这一方法用于分析山火的控制研究.
本文基于上述研究,主要给出谱负MAP(X,J)的水平与极值的联合变换的瞬时趋近算法.这一结果在实际数值计算中具有十分重要的意义,本文利用Asmussen-kella鞅,推广了MAP的波动理论,将MAP在指数时刻的相关量推广至Erlang分布的随机时刻上,继而由Erlangization方法,给定任意时刻时的MAP相应量的趋近计算式.从而解决了谱负MAP(X,J)瞬时波动理论的瞬时时间点上的计算问题.
1 谱负MAP及相关量
本文分析具有单边跳跃的MAP,具体地,设(Ω,F={Ft,t≥0},P)是完备的概率空间且满足通常条件,设(X,J)={(X(t),J(t)),t≥0}是R×E上的实值二维随机适应过程,其中E={1,2,…,N},且过程(X,J)满足:
(i)(X(t+s)-X(t),J(t+s))与Ft相互独立;
(ii)给定J(t)=i∈E,(X(t+s)-X(t),J(t+s))与(X(s)-X(0),J(s))在Pi下同分布,其中记Pi(·)=P(·|X(0)=0,J(0)=i).
于是,称过程(X,J)是MAP,其中称J为背景过程(Background process)或阶段(Phase),称X为加过程(Additive process)或水平(Level).由定义,J是状态空间为E的Markov过程,不妨设J是转移率矩阵为Q=(qij)N×N的不可约非周期的连续时间Marov过程,设J存在平稳分布π,即πQ=0,πe=1,其中e是维数适当的单位列向量.当给定J(t)=i∈E时,X是Laplace指数为ψi(α)的Levy过程Xi={Xi(t),t≥0},其中,
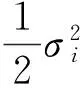
(1)
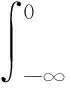
根据X的演变特点,将J的状态作如下分类:
E+={i∈E,ai>0或σi>0},记E+的势为|E+|=N+;E↓={i∈E,ai≤0且σi=0},记E↓势为|E↓|=N↓;显然N=N++N↓,为方便记述,记E+={1,2,…,N+}.符号E[A,J]表示第i行j列的元素为Ei[A,J=j]的矩阵.Ei[·]表示Pi下的条件期望.
设谱负MAP(X,J)的指数矩阵为E[eαX(t),J(t)]=eF(α)t,由[1],有
F(α)=diag(ψ1(α),ψ2(α),…,ψN(α))+Q°G(α),
(2)
其中Q°G(α)=(qijGij(α))N×N,由于谱负MAP(X,J)不具有正的跳跃,故对α≥0,F(α)是有限矩阵.
设J的初始分布为π,对固定的T>0,设:

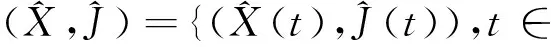
(3)
2 主要结果及证明
对x>0,定义τx=inf{t≥0,X(t)>x},称τx为谱负MAP(X,J)的首达时( first passage time),由[7],(τx,J(τx))是MAP且对应的指数矩阵为:
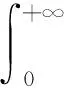
E[e-qτx,J(τx)]=(P(τx (4) 其中,eq是与谱负MAP(X,J)独立且服从分布exp(q)的R.V.,显然,过程(J(τx),x≥0)是状态空间为E+,转移率矩阵为Λ(0)的Markov过程. 定义:Π(q)=(Πij(q))N×N+,其中,Πij(q)=Pi(τ0 (5) Λ(q)和Π(q)是首达过程中两个重要的量,它给出了在服从exp(q)分布的随机时刻前,(J(τx),x≥0)在时刻τx及τ0的状态转移情况,当Λ(q)和Π(q)给定后,过程MAP(τx,J(τx))也由此确定,[7]详细地研究了Λ(q)和Π(q)的结构特点及其表示式.本文设Λ(q)和Π(q)已知,下面对这两个量进行推广. 设en,q是与谱负MAP(X,J)独立且服从Erlang(n,q)分布的R.V.,设: (6) (7) Π(n,q)=(Πij(n,q))N×N+,其中,Πij(n,q)=Pi(τ0 (8) Π(t)=(Πij(t))N×N+,其中,Πij(t)=Pi(τ0 (9) 记e1,q=eq,Λ(1,q)=Λ(q),Π(1,q)=Π(q),于是有如下引理成立. 引理1设(X,J)是如上定义的谱负MAP(X,J),则下列等式成立: (10) (11) 将上式改写成矩阵形式即为(10)式,同理可证(11)式. 引理2设(X,J)是如上定义的谱负MAP(X,J),则成立下列等式: (12) (13) 由Jagerman[17-18]反演公式,即得(12)式,同理可证(13)式. 本文的主要结果即基于此思想.下面给出Asmussen-kella鞅,它由Asmussen和kella[19]提出,是对一般指数鞅的一个推广,本文以此为研究起点,设Y(t)是紧致区间上的有限变差适应过程,设Z(t)=X(t)+Y(t),对任意初始分布的谱负MAP(X,J),设: (14) 则M(t)是均值为0的局鞅.其中ei表示第i个元素是1其他为0的维数适当的列向量. 下面给出本文的主要结论: (15) (16) 是0均值鞅,于是对上式取期望,并令t→+∞,则 (17) 因此 (18) 当J(s)∈E+时,令R(t)=-X(t)+L(t),于是,(((R(t),J(t)),t≥0))是MAP(-X,J)的单边反射过程[7],于是当R(t)=0时,对s 其中E+[·]表示初始条件为J(0)∈E+,X(0)=0的条件期望.于是, 由Fubini定理, (19) 将(18)、(19)代入(17)即得.于是定理得证. 下推论给出了谱负MAP(X,J)的水平与极值的联合变换的等式关系. 推论1 如上定理1的条件,初始水平为0的谱负MAP(X,J)满足如下等式: (20) (21) 将上式改写成矩阵形式: (22) (23) 从而有 (24) 证毕. 推论2 如上定理1的条件,初始水平为0的谱负MAP(X,J)在任意给定时刻t过程水平与极值的联合变换满足如下等式: (25) (26) 证仿引理2证明,即得. 步骤1 根据精度要求给定n; … 本文基于Asmussen-kella鞅,对一般谱负MAP(X,J)波动理论进行了推广,给出谱负MAP在与之独立且服从Erlang分布的随机时刻点上的水平与极值的联合变换所满足的等式,然后采用Erlangization方法,将这些等式转化为任意时刻处的MAP水平与极值联合变换的趋近计算式.从而解决了谱负MAP(X,J)瞬时波动理论的瞬时时间点上的计算问题.这在实际建模与应用中具有十分重要的作用. [1] ASMUSSEN S. Applied probability and queues[M]. 2nd Ed. Berlin:Springer, 2003. [3] ÇINLAR E. Markov additive processes Ⅰ[J]. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, 1972,24(2):85-93. [4] ÇINLAR E. Markov additive processes Ⅱ[J]. Probability Theory Related Fields,1972,24(2):95-121. [5] NEY P, NUMMELIN E. Markov additive processes Ⅰ. Eigenvalue properties and limit theorems[J]. Ann Probab, 1987,15(2):561-592. [6] IVANOVS J, BOXMA O, MANDJES M. Singularities of the matrix exponent of a Markov additive process with one-sided jumps[J]. Stochastic Pro Appl, 2010,120(9):1776-1794. [7] D’AURIA B, IVANOVS J, KELLA O,etal. First passage of a Markov additive process and generalized Jordan chains[J]. J Appl Probab, 2010,47(4):1048-1057. [8] D’AURIA B, IVANOVS J, KELLA O,etal. Two-sided reflection of Markovmodulated Brownian motion[J]. Stochastic Models, 2012, 28(1):316-332. [9] BREUER L. First passage times for Markov additive processes with positive jumps of phase type[J]. J Appl Probability, 2008,45(3):779-799. [10] IVANOVS J. PALMOWSKI Z. Occupation densities in solving exit problems for Markov additive processes and their reflections[J]. Stochastic Processes Appl, 2012,122(9):3342-3360. [11] KYPRIANOU A, PALMOWSKI Z. Fluctuations of spectrally negative Markov additive processes[C]//Séminaire de Probabilités XL[M]. Springer: Berlin, 2008,121-135. [12] AVRAM F, USABEL M. Finite time ruin probabilities of processes with phase type jumps[J]. Insurance, Math Economics, 2003, 32(3):371-377. [13] ASMUSSEN S, AVRAM F, USABEL M. Erlangian approximations for finite horizon ruin probabilities[J].Astin Bull, 2002,32(2):267-281. [14] STANFORD D A, AVRAM F, BADESCU A B,etal. Phase-type approximations to finite-time ruin probabilities in the Sparre Andersen and stationary renewal risk models[J]. Astin Bull, 2005,35(1):131-144. [15] RAMASWAMI V, DOUGLAS G, WOOLFORD D,etal. The erlangization method for Markovian fluid flows [J]. Ann Oper Res, 2008,160(1):215-225. [16] STANFORD D L, ATOUCHE G, WOOLFORD D,etal. Erlangized fluid queues with application to uncontrolled fire perimeter[J]. Stochastic Models, 2005,21(23):631-642. [17] JAGERMAN D L. An inversion technique for the Laplace transform with application to approximation[J]. Bell Syst Tech J, 1978,57(3):669-710. [18] JAGERMAN D L. An inversion technique for the Laplace transform[J]. Bell Syst Tech J, 1982,61(8):1995-2002. [19] ASMUSSEN S, KELLA O. A multi-dimensional martingale for Markov additive processes and its applications[J]. Adv Appl Probab, 2000,32(2):376-393. (编辑 沈小玲) A Note on Fluctuation Theory of Spectrally Negative MAP ZAHGChao-quan1*,TANGSheng-da2,QINYong-song2 (1.Department of Information Engineering, Guilin University of Aeraspace Technology, Guilin 541007, China;2.College of Mathematics, Guangxi Normal University, Guilin 541004, China) Spectrally negative MAP is one of the important contents in the probability. The fluctuation theory of the spectrally negative MAP(X,J) is generalized by the means of the Asmussen-kella martingale. The equations that satisfied by the joint transforms of the level and the extremum of the spectrally negative MAP at an independent Erlang distributed time are discussed. Furthermore, by the Erlangization method, the approximation algorithm of trancient joint transform of the level and the extremum of the spectrally negative MAP is obtained. spectrally negative MAP; fluctuation theory; Erlangization method; approximation algorithm 2012-09-08 国家自然科学基金资助项目(11271088);广西教育厅科研资助项目(201106LX067) * ,E-mail:zhangchao320@163.com O211.5 A 1000-2537(2014)02-0078-06

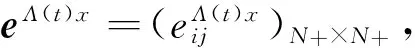
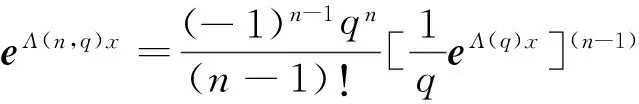
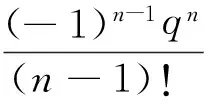
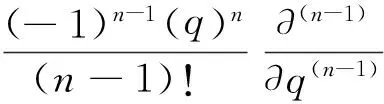
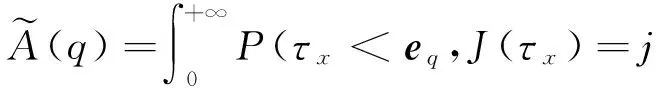

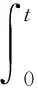
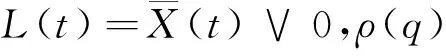
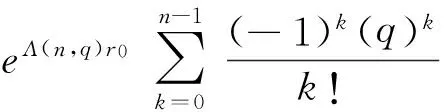

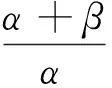

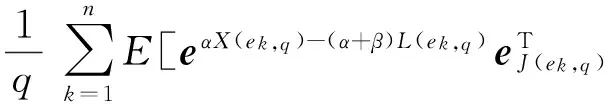
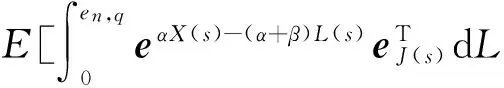






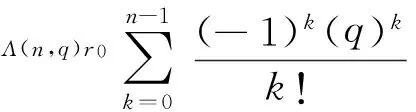

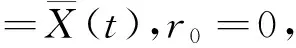
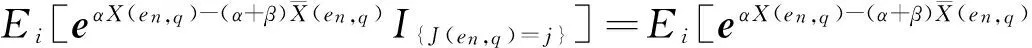
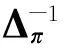
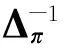



4 结论

