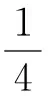一类变号三点边值问题正解的存在性
2014-09-01魏嘉*,王静
魏 嘉*,王 静
(甘肃联合大学师范学院数学系,中国 兰州 730000)
一类变号三点边值问题正解的存在性
魏 嘉*,王 静
(甘肃联合大学师范学院数学系,中国 兰州 730000)
运用锥上的Guo-Krasnoselskij’s不动点定理研究了一类非线性变号二阶三点边值问题至少一个正解的存在性.给出了与之相关联的线性二阶三点边值问题的格林函数及格林函数的一些性质.最后,作为应用,举例证明了所得结论的正确性.
边值问题;变号;格林函数;正解
近年来,由于常微分方程边值问题在工程、物理方面的广泛应用,多点边值问题受到了广泛的关注,如文[1~12] . 在文[1]中,Sun和Wei通过运用锥上的拉伸与压缩不动点定理证明了半正二阶三点边值问题
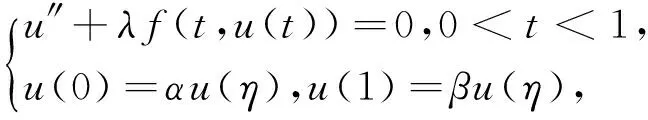
至少一个正解的存在性, 其中0<α<β<1,λ>0为参数,f:[0,1]×(0,+∞)→(-M,+∞).
本文考虑变号二阶三点边值问题
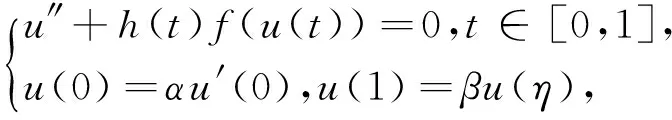
(1)
其中α≥0,0<β<1,η∈(0,1).h(t)可变号:h(t)≥0,t∈[0,η];h(t)≤0,t∈[η,1].为了讨论(1)式正解的存在性,我们做如下假设:
(H1)f∈C([0,+∞),[0,+∞)),且非减.
(H2)h∈C([0,1],R)且h(t)≥0,t∈[0,η];h(t)≤0,t∈[η,1].另外,对于[0,1]上的任一子区间,h(t)≢0.
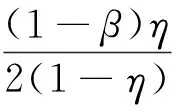
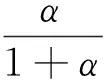
(2)
本文所用的工具为如下的Guo-Krasnoselskij,s不动点定理.
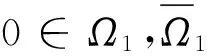
(ⅰ) ‖Au‖≤‖u‖,u∈K∩∂Ω1,且‖Au‖≥‖u‖,u∈K∩∂Ω2;或
(ⅱ) ‖Au‖≥‖u‖,u∈K∩∂Ω1,且‖Au‖≤‖u‖,u∈K∩∂Ω2,
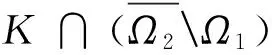
为了后面推理的需要,做如下记号:
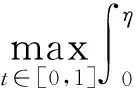
1 预备知识

引理1如果y∈E,则边值问题
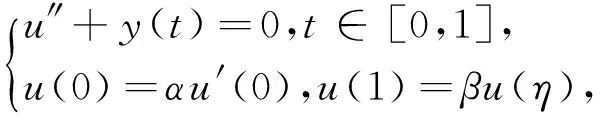
(3)
存在唯一解

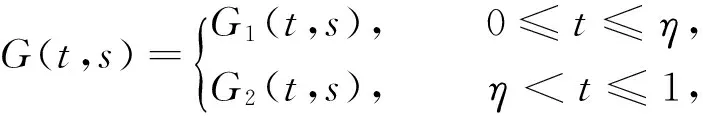
证由于边值问题(3)的唯一解可表示为
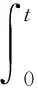
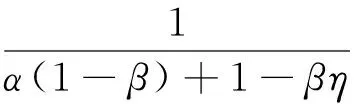
(ⅰ)当t≤η时,边值问题(3)的唯一解能够表示为
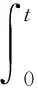
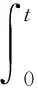
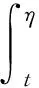
(ⅱ)当t>η时,边值问题(3)的唯一解能够表示为
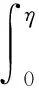

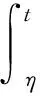
引理2格林函数G(t,s)满足如下性质:
(ⅰ)G(t,s)≥0,(t,s)∈[0,1]×[0,1];
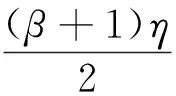
证很容易证明G(t,s)≥0,(t,s)∈[0,1]×[0,1].下面分两种情形来证明(ⅱ).
情形1, 0≤t≤η.
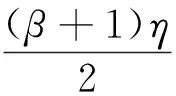
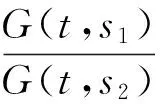
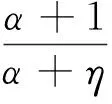
当s1∈(t,η],s2∈[η,1]时,有
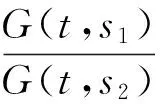
情形2,η 引理3设u∈P,则u(t)满足如下性质: (ⅰ)u(t)≥γ(t)u(η),t∈[0,η];u(t)≤γ(t)u(η),t∈[η,1],其中 证由于u∈P, 在[0,η]上u为凹的, 在[η,1]上u为凸的, 且u(0)=αu′(0),u(1)=βu(η). (ⅰ),分下面两种情况进行讨论: 当t∈[0,η]时, 有 当t∈[η,1]时, 有 从而u(t)≥γ(t)u(η),t∈[0,η];u(t)≤γ(t)u(η),t∈[η,1]. 引理4设(H1), (H2), (H3) 成立. 则对于任意的D∈[0,+∞),有 证对任意的ε∈[0,1-η],有 由于f非减,对∀ε∈[0,1-η],有 设s=η-δε,ε∈[0,1-η],对于∀D∈[0,+∞),据引理2中(ⅱ)和(H3),可得 再令s=η+ε,ε∈[0,1-η],对于∀D∈[0,+∞),有 引理5设 (H1),(H2),(H3)成立. 则算子T是全连续的. 证由于T:P→P,函数f非减, 据引理3中的(ⅰ)和引理4可得 因而 (Tu)″(t)=-h+(t)f(u(t))≤0,t∈[0,η], (Tu)″(t)=h-(t)f(u(t))≥0,t∈[η,1]. 那么由Arzela-Ascoli定理可知:T是全连续的. 定理2设 (H1)~(H3) 成立. 若如下条件之一成立, (ⅰ)f0=0 且f∞=∞ (超线性),或 (ⅱ)f0=∞ 且f∞=0 (次线性), 则变号二阶三点边值问题(1)至少存在一个正解. 证(ⅰ)假设f为超线性. 当f0=0, 存在H1>0,选取适当的θ1>0,使得对于0 令Ω1={u∈P:‖u‖ 那么 (ⅱ)假设f为次线性. 当f0=∞,存在H3>0,选取适当的θ3>0,使得对于0 令Ω3={u∈P:‖u‖ 情况一,f有界.存在ρ>0使得f(u)≤ρ,u∈[0,∞). 令H4=max{2H3,ρΔ1},Ω4={u∈P:‖u‖ 即对于u∈P∩∂Ω4,有 ‖Tu‖≤‖u‖. 考虑如下变号二阶三点边值问题 (4) 其中 [1] SUN J P, WEI J. Existence of positive solution for semipositone second-order three-point boundary-value problem [J]. Eletron J Diff Equ, 2008,41(1):1-7. [2] BAI D L, FENG H Y. Eigenvalue for a singular second order three-point boundary value problem [J]. J Appl Math Comp, 2012,38(1-2):443-452. [3] BAI Z B, DU Z J. Positive solutions for some second-order four-point boundary value problems [J]. J Math Anal Appl, 2007,330(1):34-50. [4] BOHNER M, STEVIC S. Linear perturbations of a nonoscillatory second-order dynamic equation [J], J Diff Equ Appl, 2009,15(11):1211-1221. [5] DU X S, ZHAO Z Q. A necessary and sufficient condition for the existence of positive solutions to singular sublinear three-point boundary value problems[J]. J Appl Math Comp, 2007,186(1):404-413. [6] GUPTA C P. Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equations [J]. J Math Anal Appl, 1992,168 (2):540-551. [7] KONG L J. Second order singular boundary value problems with integral boundary conditions [J]. Nonlinear Anal, 2010,31(5):2628-2638. [8] KUN W, ZHI L. Positive solutions for a system of second-order boundary-value problems involving first-order derivatives [J]. Eletron J Diff Equ, 2012,135(1):1-17. [9] LI G, LIU X, JIA M. Positive solutions to a type of nonlinear three-point boundary-value problem with sign changing nonlinearities [J]. Comput Math Appl, 2009,57(3):348-355. [10] LIU B, LIU L, WU Y. Positive solutions for singular second order three-point boundary value problems [J]. Nonlinear Anal, 2007,66(12):2756-2766. [11] MA R. Positive solutions of a nonlinear three-point boundary value problems [J]. Electron J Differential Equations, 1998,34 (1):1-8. [12] 申腾飞,刘文斌,宋文耀.一类带有p-Laplacian 算子分数阶微分方程边值问题正解的存在性[J].湖南师范大学自然科学学报, 2012,35(5):9-14. [13] GUO D, LAKSHMIKANTHAM V. Nonlinear problems in abstract cones [M]. New York:Academic Press, 1988. [14] KRASNOSELSKIJ M A. Positive solutions of operator equations [M]. Groningen: Noordhoff, 1964. (编辑 沈小玲) The Existence of Positive Solutions to Three-point Boundary Value Problem with Change of Sign WEIJia*,WANGJing (Department of Mathematics, Normal College, Gansu Lianhe University, Lanzhou 730000, China) This paper investigates the existence of at least one positive solution to the nonlinear second-order three-point boundary value problem with change of sign by the application of the Guo-Krasnoselskij’s fixed-point theorem in cones. The Green’s function and some of its properties of the linear second-order three-point boundary value problem related to the nonlinear boundary value problem are provided. At last, an example is given to demonstrate the results of this study. boundary value problem; sign changing; Green’s function; positive solution 2012-11-05 甘肃省自然科学基金资助项目(3ZS042-B26-021);甘肃省教育厅科研基金资助项目(1013B-03) * ,E-mail:weijia_vick@163.com O175 A 1000-2537(2014)02-0072-06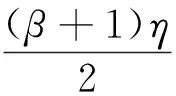
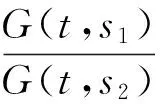
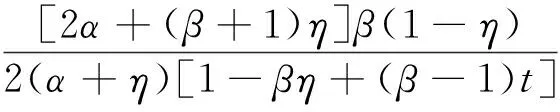
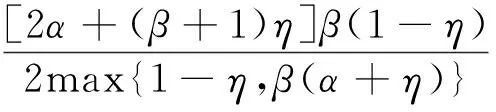
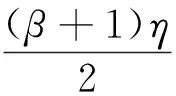
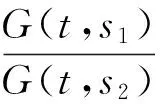
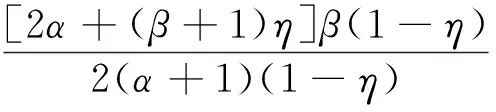
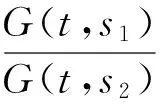
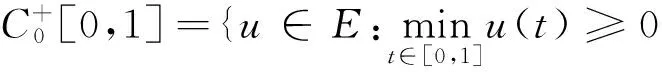
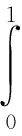
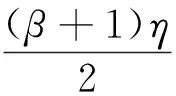

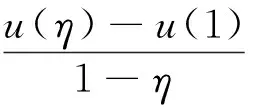
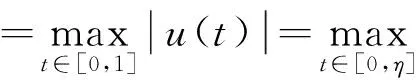
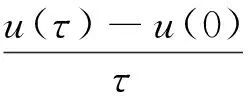


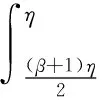
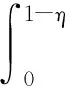
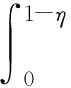
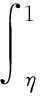
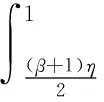
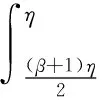

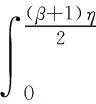
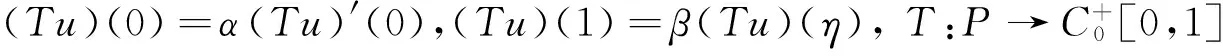
2 主要结果

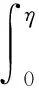
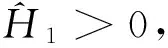
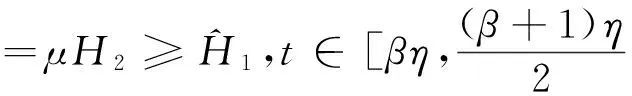
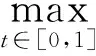
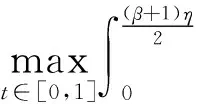
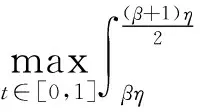
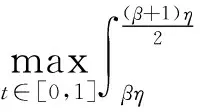
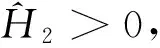
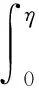
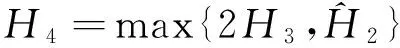
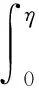
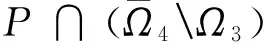
3 应用举例