资源能力受限的需求非平稳有限阶段订货模型

王怡青

(华北水利水电大学 软件学院，河南 郑州 450045)

资源能力受限的需求非平稳有限阶段订货模型

王怡青

(华北水利水电大学 软件学院，河南 郑州 450045)

通过对Wagner-Whitin方法的约束条件扩展，得到了改进的Wagner-Whitin方法，使其能够解决资源能力受限的需求非平稳订货问题.对无资源受限的需求非平稳订货、资源约束恒定的需求非平稳订货和资源约束周期变化的需求非平稳订货3种情况进行实例仿真和数值分析，得出在无资源约束时订货成本最小，随着资源约束量限度的增加，订货成本会阶段性减少等结论.

资源能力受限；需求非平稳；Wagner-Whitin；有限阶段订货

订货批量问题[1]是企业在制定订货计划时，确定在给定计划范围T内的各个订货时间段的物资订货量问题.EOQ经济订货模型[2]是解决该问题的著名方法，但前提是物资的需求量恒定不变.企业在制定物资供应计划的过程中，会先参考由其他部门提供的物资需求计划，此时的物资需求计划往往都是随着工程进度不断变化的，这时便不能用经典的EOQ经济订货模型来制定相应的订货计划.对于这种需求非平稳的订货问题，1958年, Wagner和Whitin提出了动态批量问题的动态规划算法即Wagner-Whitin方法[3-4](以下简称WW算法)，它是解决此类问题的最优方法.但在有些情况下，会出现资源紧张或供应商供应能力不足的情况，此时企业在制定供应计划时会考虑资源能力的约束，而WW算法只能解决无资源约束下的需求非平稳订货问题.

本研究的主要工作就是在WW算法的基础上进行新的约束条件扩展得到改进的WW算法，使其能够解决有资源约束的需求非平稳订货问题.同时，考虑到实际的资源约束情况，对资源约束进行分类研究，即资源约束恒定和资源约束周期变化两种情况，分别给出相应的算法.结合实例进行计算机仿真，对几种情况进行比较和数值分析，得出一般性的结论.

1 问题描述和模型的建立

先考虑资源能力约束恒定的情况，能力受限的资源非平稳订货问题的数学模型如下：

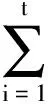
(1)

s.t.V0=0,Vi=0.

(2)

(3)

0≤Qi≤Φ,i=1,2,…,t.

(4)

(5)

Hi(Vi)=vrVi.

(6)

Qi为整数,i=1,2,…,t.

(7)

其中,已知量有t—在整个计划范围T内总共的订货阶段个数，Di—第i个阶段内对物品的需求量且各个阶段Di不同，Φ—在整个时间周期t内的资源约束量，是一个常数；决策变量有Vi—第i个阶段末的物品库存量，Qi—第i个阶段初的订货量.

模型中,式(1)为目标函数，即总费用成本F(t)最小，包括整个订货时间周期t内的订货费和存储费；式(2)代表初始和终结库存量约束，即要求初始和结束周期的库存为0状态；式(3)代表库存量约束，即不允许缺货；式(4)代表资源能力约束，即每次订货量都不得超过Φ；式(5)为第i阶段的订货费，不随订货量Qi变化；式(6)为第i阶段的存储费，它与单个周期内的库存量Vi成正比，其中vr为单位库存成本；式(7)保证订货量符合实际情况.

2 改进的WW算法和问题扩展

2.1改进的WW算法

在无资源约束的情况下，由WW算法可得到最优解,其目标函数递推方程为

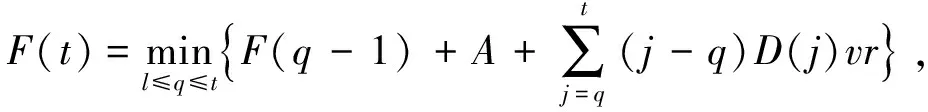
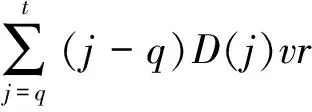
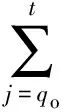
(8)

WW算法只考虑了无资源能力约束时的订货，增加资源能力约束后便不能用来求解.对其进行改进，增加约束条件，在新的求解范围内对目标函数继续运用动态规划的思想进行求解，得到改进的WW方法.具体如下：

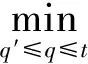
同上，用动态规划递推原理选择合适的订货点q0，如式(9)所示,且q0∈[q′，t]，使F(t)最小，

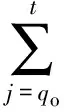
(9)

经过计算,可以得到此算法的计算复杂度为O(T2).

2.2问题扩展

在实际订货问题中,还可能会遇到资源能力约束不为常量的情况，即约束量会随着订货时段的推移周期变化.设一次资源能力变化的周期为T，已知Φ(1)，Φ(2)，…，Φ(T),则可行的订货时段集合为

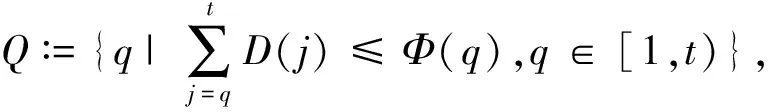
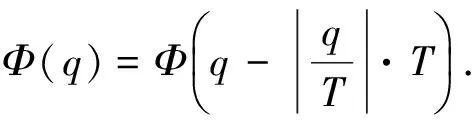
此时,目标函数递推式变为

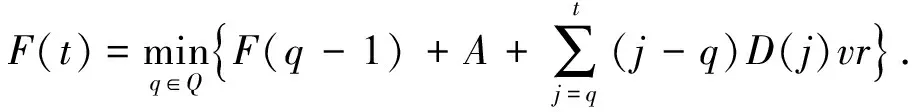
同上,在可行订货时段Q内，根据动态规划递推法，选择合适的订货点q0，使总费用F(t)最小.

3 数值算例

上述算法采用C语言实现.为了对比3种情况对订货策略和库存量的影响，采用t=12总周期的需求非平稳的数值算例，分别对其进行了仿真，计算结果分见表1至表4.其中,表1至表3为3种情况的具体订货策略，表4为3种情况的最终成本及其他标准的比较.

表1 无资源约束情况下的订货策略和库存量Tab.1 The ordering strategy and inventory with unconstrained of resource

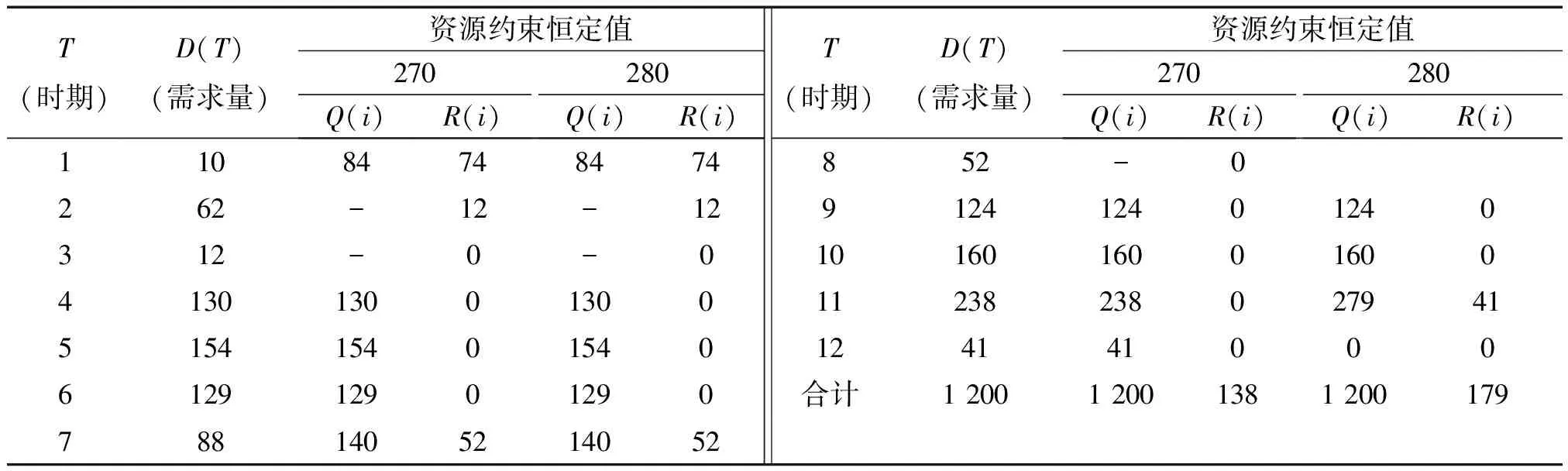
表2 资源约束恒定情况下的订货策略和库存量Tab.2 The ordering strategy and inventory with constant capacitated of resource

注：资源约束恒定量分别为270个和280个单位.

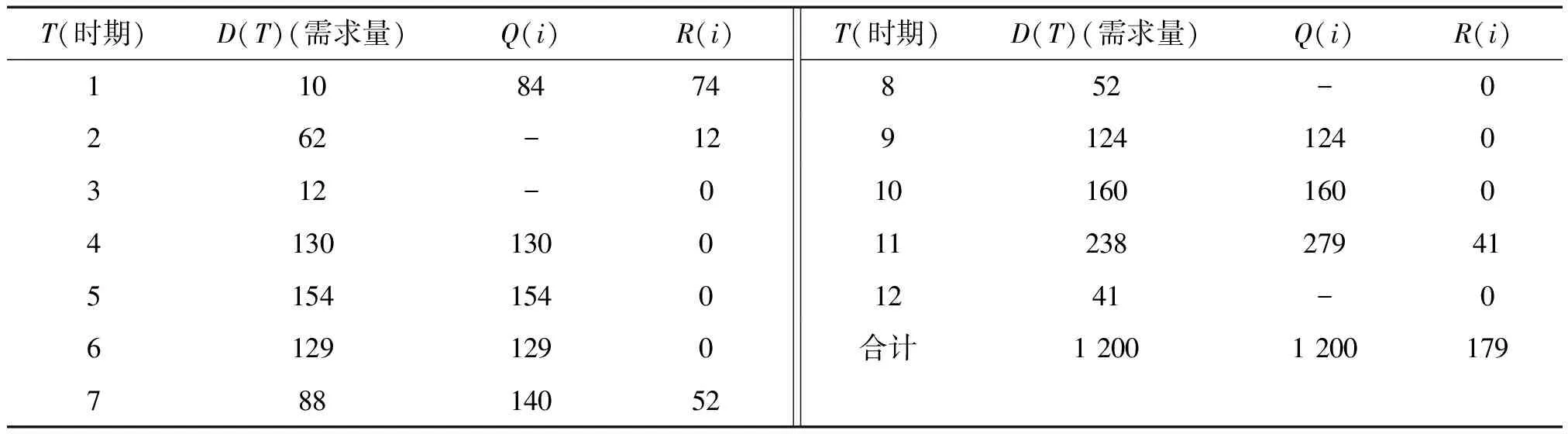
表3 资源约束周期变化情况下的订货策略和库存量Tab.3 The ordering strategy and inventory with periodical changed capacitated of resource

注：资源约束量周期变化为{250,280,200,350,300}，每次变化持续的单位阶段长度T为 { 3，2，4，1，2}.

表1和表2表明：

(1)资源约束量的最小值要能够满足当前阶段的需求量.具体地说，当资源约束量恒定时，其最小限度要能够满足整个计划范围内的最大需求量；当资源约束量呈周期性变化时，资源约束量要能够满足其自身持续时间内的最大需求量，否则无法由改进的WW算法求得结果.这是由于WW算法本身的前提是最低满足一个阶段的需求量，如果这个条件得不到满足，动态规划的递推条件就不能满足，则无法求解.

(3)存在资源能力约束时(不论恒定或周期变化)，只要资源约束量能够满足在无资源约束时所得到的订货策略中的最大订货量(如此例中在无约束时得到的最大订货量为283)，则不论之后资源约束量再如何变大，将不对最后结果有影响，即得到的订货成本和订货策略都相同，且均为最优值(和无约束情况的结果相同).这是由于在有资源约束量存在的情况下，一旦资源约束量满足了无资源约束时所需订货量的最大值，则在整个计划周期内，其他阶段所需的订货量都会被满足，此时订货点的选择范围又完全等同于无约束情况，故所得的最终结果和无约束相同，之后不受资源约束量的影响.

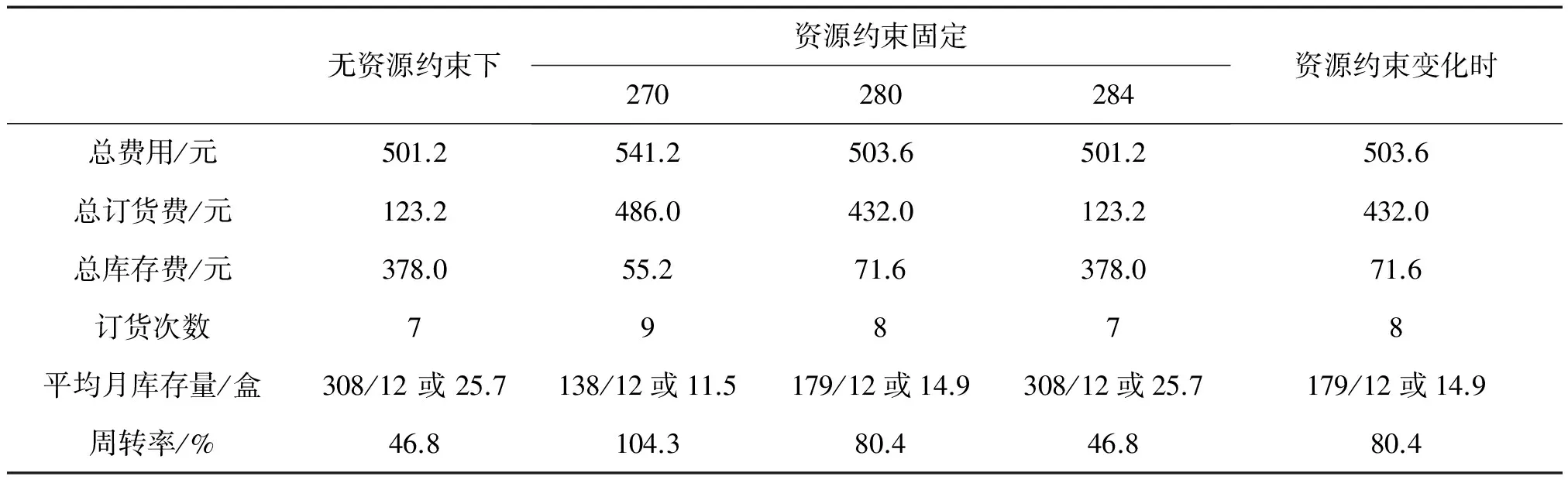
表4 3种情况的计算结果比较Tab.4 The comparison of the three cases’ calculation results

由表4可知,无资源约束时的订货总成本最小；资源约束增加后，总费用成本相应增加.这3种情况下,WW算法所得的结果均为最优值，所得订货策略最佳.

4 结束语

针对资源能力受限的需求非平稳订货问题进行了研究，通过对经典Wagner-Whitin方法进行新的约束条件扩展，使其可以解决该类订货问题.同时,分别对资源约束恒定和资源约束周期变化的两种情况予以讨论，提出了相应的数学模型和解决方法.通过对3种情况的实例仿真分析，可以看出无资源约束时的订货成本最小；当存在资源约束量时，随着约束量限度的增加，订货成本减少，但当约束增加到一定程度时，对最后总费用成本没有影响.

由Wagner-Whitin方法来解决无资源约束和存在资源约束的需求非平稳的订货问题，所得的结果都是最优解和最优订货策略.但其计算复杂度比较大，而类似Silver-Meal的启发式方法[5]的计算量就相对偏小，求解结果在某些情况下与Wagner-Whitin方法接近，在后续的工作中将对这些问题进行深入探讨.

[1] Chuda B,Janny M Y L.Inventory lot-sizing with supplier selection[J].Computers & Operations Research,2005(32):1-14.

[2] Silver E A,Peterson R.Decision Systems for Inventory Management and Production Planning[M].New York: John Wiley & Sons,1985.

[3] Wagner H M,Whitin T M.Dynamic version of the economic lot size model[J].Management Science,1958(5):89-96.

[4] 张鲲，滕国库.巧用Wagner-whitin和启发式算法实现变质库存管理模型[J].琼州学院学报，2009(5):38-40.

[5] Silver E A,Meal H C.A heuristic for selecting lot size quantities for the case of a deterministic time varying rate and discrete opportunities for replenishment[J].Production and Inventory Management,1973(14):64-74.

Limitedstagesuppliesreplenishmentmodelwithresourceconstrainedandvariabledemand

WANG Yi-qing

(SchoolofSoftware,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450045,China)

This paper studies the limited stage supplies replenishment model with resource constrained and variable demand. We extend the constraints of Wagner-Whitin model so that the improved algorithm can solve the problem. Based on computational experiments and numerical analysis of three conditions of the supplies replenishment problem with variable demand-uncapacitated, constant capacitated, and periodical changed capacitated, we conclude that the cost is minimum when there is no restriction on resource , and the cost will decrease discretely with the increasing restriction.

resource capacitated; variable demand; Wagner-Whitin; limited stage

2014-05-15

王怡青(1983-)，女，河南许昌人，助教，硕士，主要从事系统工程与商业智能方面的研究.

TP311

A

1674-330X(2014)03-0044-04