离心泵转子动力学模型中流体力的简化

蒋爱华，华宏星，陈长盛，李国平，周 璞，章 艺

（1.中国船舶重工集团公司 第704研究所，上海200031；2.上海交通大学 机械系统振动国家重点实验室，上海200240）

离心泵转子动力学模型中流体力的简化

蒋爱华1，2，华宏星2，陈长盛1，李国平1，周 璞1，章 艺1

（1.中国船舶重工集团公司 第704研究所，上海200031；2.上海交通大学 机械系统振动国家重点实验室，上海200240）

采用叶轮流体力的简化方式可以提高离心泵流体激励诱发振动的计算的准确程度。根据达朗伯原理对试验台架建立了包含离心泵基座的四圆盘三轴段转子动力学模型；将流体力分别简化为叶轮内20%流体质量、40%流体质量、CFD集中力与力矩，采用Newmark—隐式算法对转子动力学模型进行瞬态响应分析。结果表明，将叶轮上流体力简化为CFD；所得集中力与力矩时；可有效得出离心泵运转过程中流体激励所诱发的基座振动。而所获得的基座振动位移与加速度幅值均远大于将流体力简化为叶轮内20%或40%流体质量所获得的基座振动数值。另一方面，将流体力简化为叶轮内40%流体质量所获得的基座振动大于简化为叶轮内20%流体质量所获得的基座振动。

振动与波；离心泵；流体激振；转子；Newmark-β隐式算法；

在叶轮机械转子动力学建模中，通常不考虑流体激励的实际过程，而将流体对叶轮的激励力简化为叶轮的附加质量，该附加质量为叶轮内所包含流体20%～40%的质量，而后计算此转子模型其它外激励作用下的振动情况或临界转速[5,6]。这种方法可以不用计算真实的流体激励力，而只需从结构力学的角度考虑系统的振动特性，因此工程中得到了广泛的应用[7]。

随着CFD计算的发展，计算轴系转动过程中离心泵叶轮所受到的流体力成为可能[8—13]。

已有将叶轮表面所受分布流体力积分成叶轮轴向与径向的集中力与集中力矩的研究[14,15]，但还没有将所得轴向与径向集中力作为外激励作用于转子动力学模型并计算转子振动，更没有对这几种流体激励力处理方式所得结果进行对比，因而，也无法确定采用何种流体激励力处理方式才可得更加理想结果。

鉴于以上原因，本文将建立包含离心泵叶轮—转轴—轴承—基础的转子动力学模型，对以上流体激励力处理方式进行对比分析研究。

1 离心泵转子试验台架

本文的研究对象为一单级单吸含六个扭曲叶片的离心泵，叶轮直径为172 mm，其额定工况下比转速为139，额度转速为2 930 r/m in（48.83 Hz），额定流量为100 t/h。

建立了离心泵转子试验平台，离心泵系统安装情况如图1所示，垂直于离心泵机架方向为图中的+ X向。

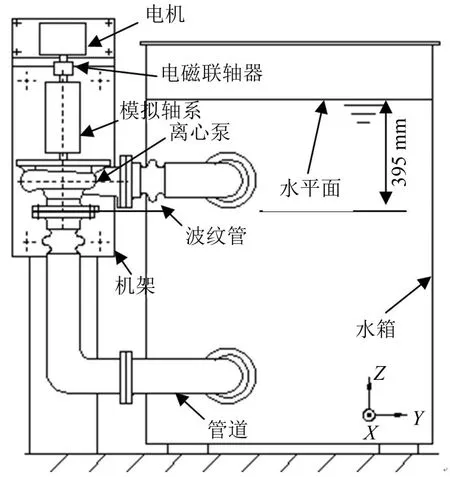
图1 离心泵安装示意图

电机通过非接触式电磁联轴器带动模拟轴系（模拟实际电机离心泵安装情况）与离心泵叶轮转动，离心泵通过管道吸入水并将水送回到水箱中；

模拟轴系与支架之间采用滚动轴承连接；离心泵、模拟轴系与电机安装与同一机架上，机架通过八个隔振器安装于刚性基础上；

离心泵进出口通过波纹管与管道相连接以隔离管道振动，从而使电机—模拟轴系—离心泵—机架成为一个独立的振动系统；

电磁联轴器的作用是仅传递扭矩而消除电机转轴与模拟轴系不对中引起的系统振动；通过动平衡技术减小了电机主轴的质量不平衡。

2 转子模型的简化

如图2所示为电磁联轴器—模拟轴系—支撑—离心泵—基础系统的剖视图。依据其实际结构建立了包含基座的四圆盘三轴段转子动力学模型。

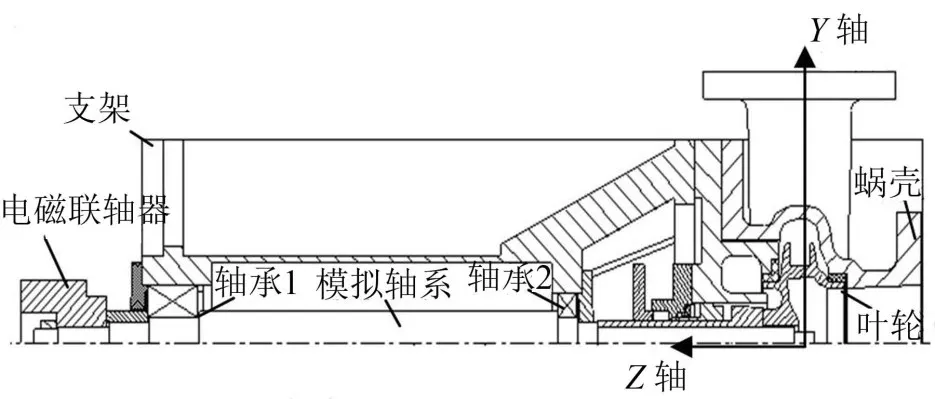
图2 轴系对称平面的半剖视图

由于电磁联轴器、叶轮的直径远大于转轴直径，因此在进行模化时将其考虑成为质量圆盘；同时将轴承与转轴自身也简化成为轴承处的两个圆盘；

转子与支架之间采用滚珠轴承连接，由于滚珠轴承阻尼较小，因此将其直接简化成为弹簧，同时由于隔振器阻尼较小，也忽略其阻尼作用；

支架、蜗壳、电机、电机与支架共同机架则简化成为转子—轴承系统的基座并用质量块代替，隔振器也简化成为弹簧并将基座与刚性基础相连接；

建模时，忽略转子的扭转振动和剪切效应，仅研究转子的弯曲振动。

根据如图2中所示结构建立了包含基础的四圆盘三轴段的转子动力学模型，由于以+X向的转子模型进行流体力简化方式的研究；简化所得+X向转子模型如图3中所示，其中圆盘4对应叶轮，表1、2中分别列出了转子模型中轴段、圆盘与基座的具体参数。

表1 转子模型中轴段参数

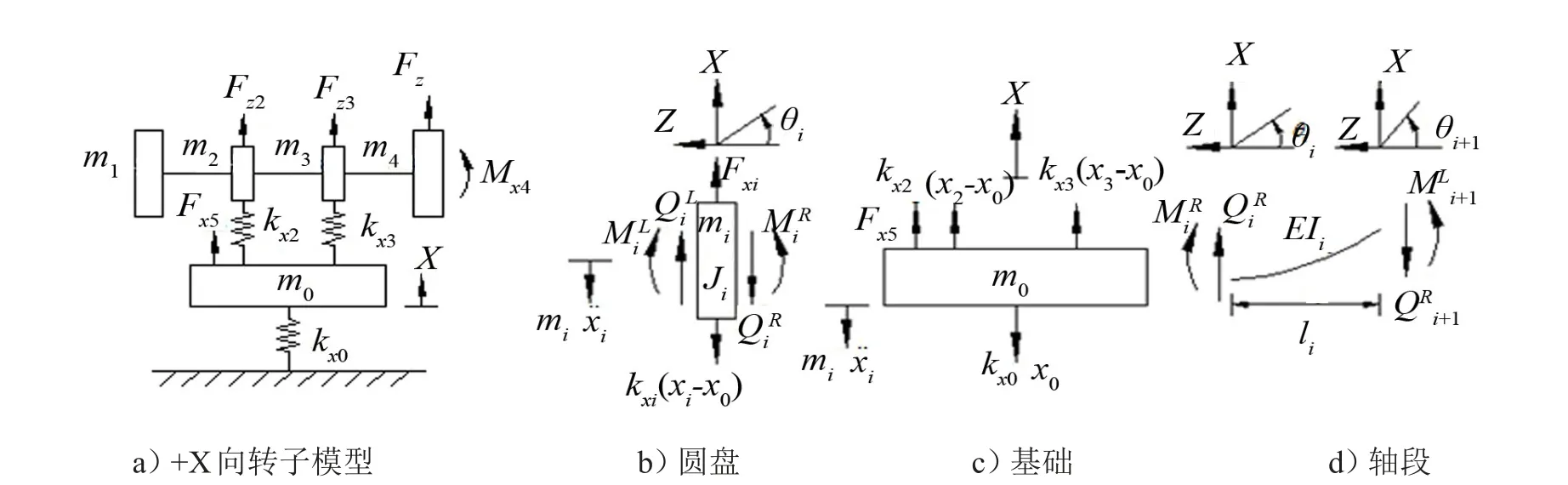
图3 转子模型的简化

表2 转子模型中圆盘与基座参数

基于达朗伯原理建立了转子动力学方程如式（1）所示

X、F、M与K的具体形式为

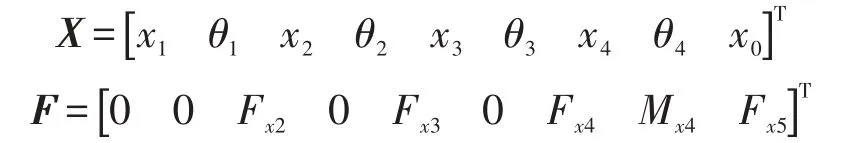
X向量中xi、Ɵi分别圆盘i的位移与绕X轴转角；F向量中Fx4、Mx4分别为叶轮上流体力与力矩；M矩阵中mi、Ji分别为圆盘i的质量与绕径向的转动惯量，m0为基础的质量，包含了；K矩阵中，li为轴段i的长度，kx0为八个隔振器的并联刚度，kx2与kx3为轴承的支撑刚度。

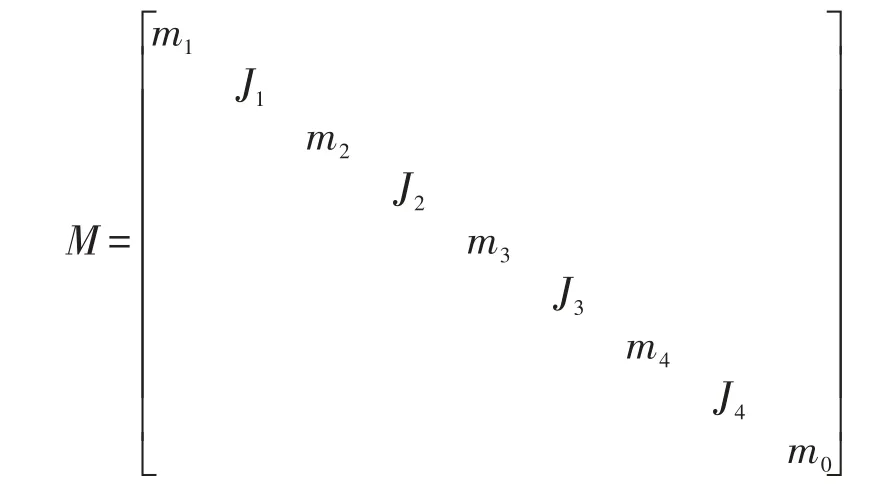
模型中轴承的支撑刚度kx2与kx3采用在轴系上轴承附加的增加配重，并测试附加配重前后轴承处轴系振动位移的变化量计算得出，测得电磁联轴器端轴承刚度为7.50×106N/m，叶轮端轴承刚度为4.01×106N/m。如图4所示为轴承刚度测试传感器布置图。

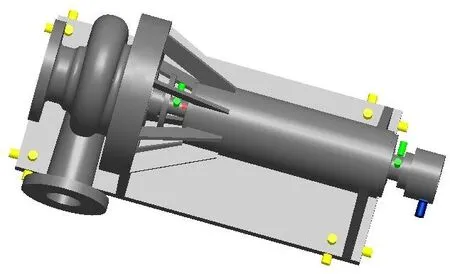
图4 轴承刚度测试传感器布置

测得联轴器端轴承刚度约等于两倍叶轮端轴承刚度，这与离心泵端采用了一个轴承、联轴器端采用了两个轴承的实际结构相符。

模型中其余参数均根据轴系的实际质量、转动惯量与结构尺寸得出。

3 离心泵叶轮流体力的分析

运用Por-E建立离心泵内各流体域模型，包括离心泵进口流域、叶轮内流域、蜗壳内流域、平衡室流域、叶轮前盖板与蜗壳间隙流域（包括泄漏环处间隙）、叶轮后盖板与蜗壳间隙流域与蜗壳出口延长段流域共七个流体域。

各流域网格划分均采用ICEM完成，所划分网格均为六面体，而后将各流域网格导入CFX中通过interface界面连接为一个整体。

计算时进口边界条件为静压3 871 Pa（亦即395 mm水柱），出口边界条件设置为流量，湍流模式了采用SST模式。

采用基于有限体积法的CFX首先对离心泵内流场进行稳态分析，而后将稳态分析结果作为瞬态分析初始值，以叶轮每转动2度为一个时间步，运用CFX分析了离心泵按照额定工况运转一周过程内180个时间步的瞬态流场。

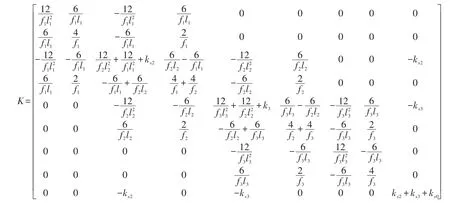
最终由计算所得叶轮各表面的流体力，积分得出叶轮转动一周过程中空间三个方向上的流体集中力与集中力矩，积分可直接在CFX中完成，其中叶轮+X向流体集中力与绕Y轴的集中力矩如图5中所示，各方向定义如图1、2中所示。

文献[14、15]中对本文中叶轮所受流体力计算过程与结果正确性的验证有更详细描述。

4 不同流体力处理方式振动的对比

4.1 转子动力学模型瞬态响应分析方法

根据所建立的转子动力学模型，将叶轮上流体力分别简化为20%叶轮内水质量、40%叶轮内水质量，以及CFD所获得流体集中力与力矩三种处理方式，对模型进行瞬态响应分析。

瞬态响应分析时，在圆盘3上增加了初始相位为0，幅值与+X向流体力最大幅值相同的正弦激励，激励频率为叶轮的转动频率。

前两种流体力的处理方式是将其作为模型的附加质量，即在式（1）所示转子动力学模型中增大M4，第三种方式则是将流体力作为模型的激励进行分析，该激励作用于圆盘4上，与圆盘3上正弦激励力共同作用于转子模型上。

叶轮中水的质量为0.7 kg，在三种处理方式中均保留了绕X轴流体集中力矩。

采用Matlab编译的Newmark-β隐式算法对转子动力学方程进行了瞬态响应求解。通过激振力延拓的方式对转子模型重复加载，共计算了叶轮转动100圈过程中共18 000个时间步过程中系统的振动响应。

采用CFD所获得流体力对转子模型进行加载时方式如下：以10 s作为第一个载荷步的加载时间，并保持该载荷5 s，而后再以CFD计算中所使用时间步长循环加载+X向集中力、绕Y轴集中力矩以及正弦激励。

采用这种加载方式是为了降低CFD所得第一个时间步流体力阶跃效应的响应频率，而后运用Buttworth六阶滤波器滤出了10 Hz以下的信号，则可以消除第一个时间步阶跃激励的影响。第一个时间步流体力数值不为零，零时间直接加载相当于1阶跃激励，因转子模型中未加入阻尼的作用，该阶跃响应将一直存在，因此需进行高通滤波处理。

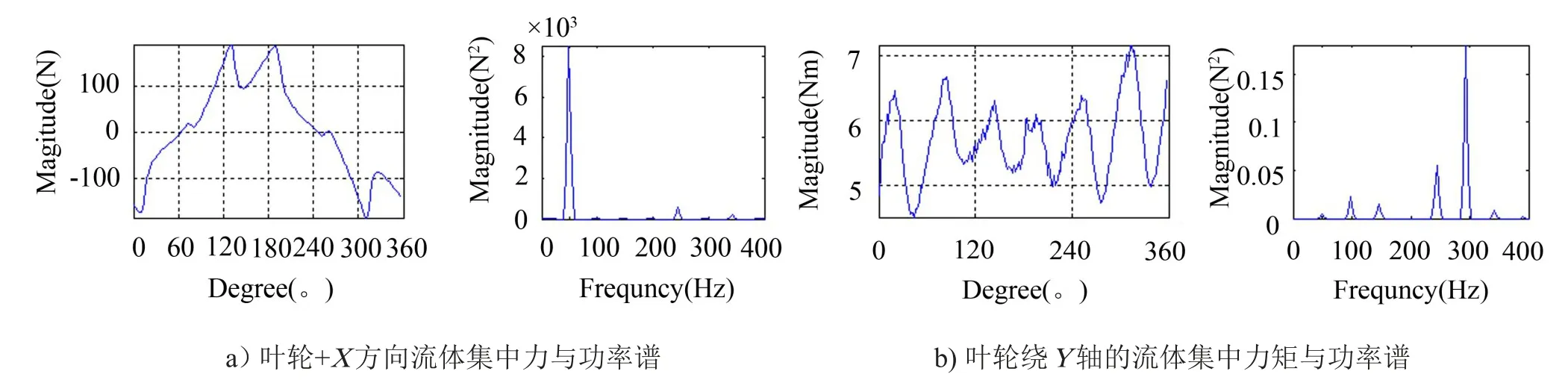
图5 离心泵叶轮流体力的计算结果

4.2 转子模型的验证

通过试验测试所得离心泵运转过程中支架上的振动信号，对比转子模型瞬态响应分析中基座的振动信号，以验证转子模型的正确性。

振动测点布置如图4中测点1、2、3、4所示。对测得结果进行了算术平均。

对转子模型进行瞬态响应分析的方法如上所述，但圆盘3上+X向激振力幅值设为0，以模拟离心泵轴系的实际工作情况。

如图6所示即为离心泵运转5 m in内基座振动位移与加速度测试结果的算术平均，对比计算所得基座振动位移与振动加速度的时域与频域波形。

从图中可以看出计算所得振动位移幅值虽然小于测试振动位移，但二者时域波形形状基本一致，频域最大峰值均出现于48.8 Hz处，且幅值接近；振动加速度时域波形幅值相近，最大峰值均出现于244.2 Hz处（5倍转频），因此可认为所建立的转子动力学模型是有效的。

计算结果与测试结果误差的主要原因一是未计入轴系自身不平衡所诱发的振动；二是忽略了电机传递至支架上的振动，但所建立的模型在分析不同流体力处理方式仍将是有效的。

4.3 不同流体力处理方式分析结果对比

以所建立转子模型中基础的振动对流体力以上三种处理方式进行对比分析。

如图7所示为圆盘3上作用幅值与+X向流体力最大幅值相同的正弦激励时，三种不同流体力处理方式下最后3个周期转子模型中基座的振动位移与加速度，以及20个周期基座振动位移与加速度的功率谱。

从振动位移时域图与功率谱中可以看出，将流体激励力简化为20%或40%叶轮中水的质量，并以其作为附加质量作用于叶轮上时，所得到的振动位移幅值明显小于采用CFD所得流体力作用于叶轮上所得到的振动位移幅值。

以20%叶轮中水质量作为附加质量时的基座振动位移幅值小于以40%叶轮中水质量作为附加质量时的基座振动位移。

三种处理方式振动位移功率谱最大峰值均出现于离心泵转频48.8 Hz处；与转频处峰值相比，离心泵叶频处的峰值并不明显。

从振动加速度时域图与功率谱中可以看出，将流体激励力简化20%或40%叶轮中水质量的附加质量时，基座振动加速幅值也均小于CFD流体力所获得的基座振动加速度幅值，且其对比结果比振动位移更加明显；

以20%叶轮中水质量作为附加质量时的基座振动加速度幅值也小于以40%叶轮中水质量作为附加质量时的基座振动加速度；

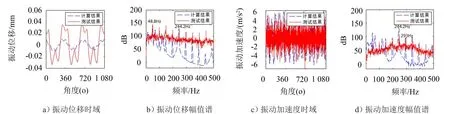
图6 测试与计算所得基础振动对比

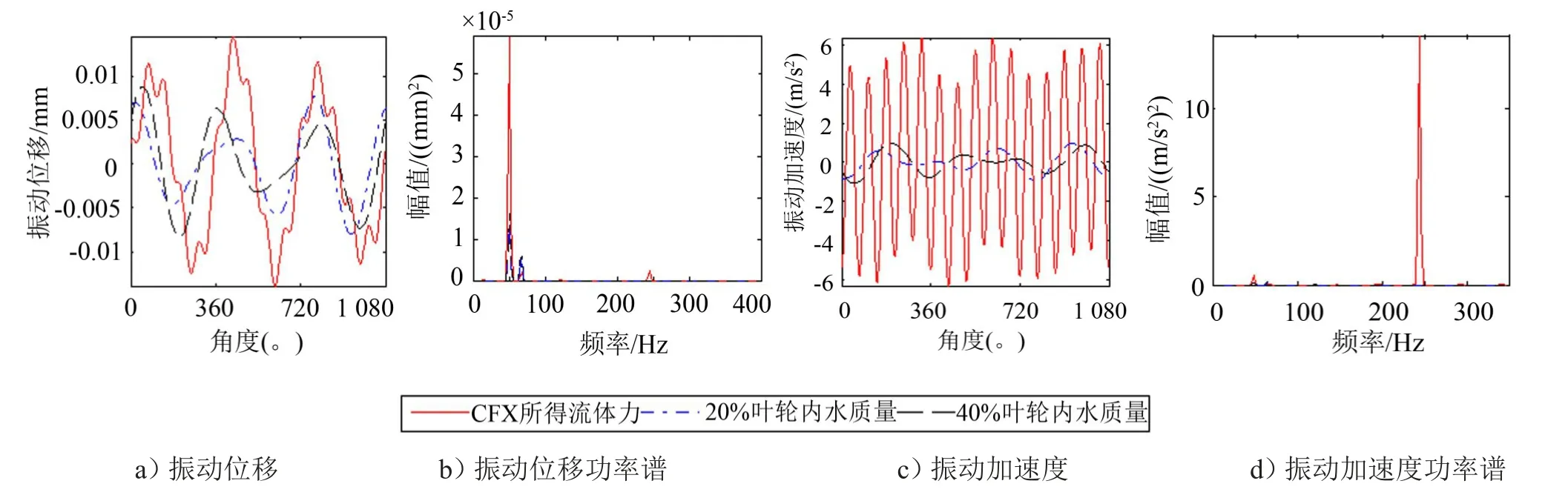
图7 流体激励力不同处理方式基础响应对比

将流体力简化为附加质量时，在叶轮转频外激励作用下，其振动加速度功率谱最大峰值位于叶轮转频处，但峰值相对较小，而CFD流体力作用下基座振动加速度功率谱最大峰值则位于5倍转频处。

出现5倍转频是因为CFD所得叶轮+X方向流体集中力与绕Y轴的集中力矩存在5倍转频分量，而在该频率处出现峰值原因可作为进一步研究的内容。

5 结语

从以上对比分析结果可以得出如下结论：

(1)将叶轮上流体力简化为CFD所得集中力与力矩可有效得出离心泵运转过程中流体激励所诱发的基座振动；

(2)将流体力简化为CFD所得叶轮上集中力与力矩所获得的离心泵基座振动位移与加速度幅值均远大于将流体力简化为叶轮内20%或40%流体质量所获得的基座振动；

(3)将流体力简化为叶轮内40%流体质量所获得的离心泵基座振动大于简化为叶轮内20%流体质量所获得的基座振动；

(4)所建立的含离心泵基座的转子动力学模型是有效可靠的；所建立的离心泵试验台架能够有效验证对比不同流体力简化方式的准确性；

(5)采用更加准确的轴承刚度测试方法，考虑陀螺力矩效应将能够使计算计算结果更接近于真实值；可通过以上研究方法对其它方向流体力简化方式进行验证。

[1]蒋爱华，张志谊，章 艺，等.离心泵噪声研究的综述和展望[J].振动与冲击，2011(2)：77-84.

[2]张 浩，冯 涛，刘碧龙，等.离心泵流噪声实验研究[J].振动与噪声控制，2013(1)：119-122.

[3]Ji Pei,Shouqi Yuan,Jianping Yuan,et.Numerical analysis on asymmetrical distribution of flow field and radial force for a centrifugal pump[C].2009 International Conference on Energy and Environment Technology.2009:741-744.

[4]Blanco Eduarde,Parrondo Jorge,Barrio Raúl,et.Fluiddynamic pulsations and radial forces in a centrifugal pump w ith different impeller diameters[C].Proceedings of 2005 ASME Fluids Engineering Division Summer Meeting, 2005:1634-1643.

[5]袁振伟，楮福磊，林言丽，等.考虑流体作用的转子动力学有限元模型[J].动力工程，2005(8)：457-461.

[6]孙启国，虞 烈.流体机械中浸液转子动力学特性的研究[J].动力工程，2000(10)：906-909.

[7]闻邦春，顾家柳，夏松波，等.高等转子动力学[M].北京：机械工业出版社，2000.

[8]李 伟，施卫东，蒋小平，等.多级离心泵轴向力的数值计算与试验研究[J].农业工程学报，2012(28)：52-58.

[9]José G,Jorge1 P,Carlos S,etc.Steady and unsteady radial forces for a centrifugal pump w ith impeller to tongue gap variation[J].Journal of Fluids Engineering,Transactions of the ASME,2006(5):454-462.

[10]Benra Friedrich-Karl,Dohmen Hans Josef,Schneider Oliver.Calculation of hydrodynam ic forces and flow induced vibrations of centrifugal sewage water pumps[J].Proceedings of the ASME/JSME Joint Fluids Engineering Conference,2003(1):603-608.

[11]施卫东，李启锋，陆伟刚，等.基于CFD的离心泵轴向力计算与试验[J].农业机械学报，2009(1)：60-63.

[12]祝 磊，袁寿其，袁建平，等.阶梯隔舌对离心泵压力脉动和径向力影响的数值模拟[J].农业机械学报，2010 (9)：21-26.

[13]黄国富，常 煜，张海民.基于CFD的船用离心泵流体动力振动噪声源分析[J].水泵技术，2008(3)：20-33.

[14]蒋爱华，章 艺，靳思宇，等.离心泵流体激励力的研究：蜗壳部分[J].振动与冲击，2012(4)：60-66.

[15]蒋爱华，章 艺，靳思宇，等.离心泵叶轮流体激励力研究[J].振动与冲击，2012(22)：123-127.

Simplification of Fluid Force in Rotordynam ic Model of Centrifugal Pumps

JIANG Ai-Hua1,2,HUA Hong-Xing2，CHEN Chang-Sheng1, LI Guo-Ping1,ZHOU Pu1,ZHANG Yi1

(1.704 Rsearch Institution,China Shipbuilding Industry Corporation,Shanghai 200031,China; 2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)

Simplification of the fluid force applied on impeller can significantly raise the accuracy of computation of centrifugal pump vibration incited by the fluid.In this paper,a rotor dynam ic model including four discs,three shaft sections and a pump base is built for the workbench based on D'Alembert principle.Then fluid force on the impeller is simplified as 20%fluid weight in impeller,40%fluid weight in impeller,and a concentrated force as well as a torque by CFD respectively.Finally,the transient response analysis is carried out by Newmark-implicit algorithm.The result shows that the base vibration incited by the fluid force during centrifugal pump operation can be effectively gained by simplifying the fluid force on the impeller to a concentrated force and a torque,and the amplitudes of acceleration and displacement of the base vibration by simplifying the fluid force to concentrated force and torque are much larger than those by simplifying the fluid force as 20%and 40%fluid weight in the impeller respectively.Also,the acceleration and displacement amplitudes by 40%fluid weight in the impeller are larger than those by 20%fluid weight in the impeller.

vibration and wave;centrifugal pump;vibration incited by fliud;rotordynam ics;Newmark-βimplicit algorithms

1006-1355(2014)04-0077-06

TB53；TH432 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.017

流体激励力是离心泵振动的主要原因之一，由于离心泵的叶轮与转轴—轴承—基座连接于一体，流体激励诱发其转子系统振动的机理也相对复杂[1—4]。

2013-10-24

蒋爱华（1980-），男，四川达州，博士，研究方向为流体激励诱发的振动。

E-mail:jiang198011@163.com