吊挂刚度对车体和设备模态的影响

高荣荣，张立民，邱飞力，班希翼，孙现亮

（1.西南交通大学 牵引动力国家重点实验室，成都610031；2.南车青岛四方机车车辆股份有限公司，山东 青岛266111）

吊挂刚度对车体和设备模态的影响

高荣荣1，张立民1，邱飞力1，班希翼1，孙现亮2

（1.西南交通大学 牵引动力国家重点实验室，成都610031；2.南车青岛四方机车车辆股份有限公司，山东 青岛266111）

模态是车辆的一项重要特性，包括车体模态和吊挂设备模态，各阶模态频率随着各种因素的变化而有所不同。为考虑车体弹性模态，将车体等效为欧拉伯努利梁。在某型高速列车有限元模型基础上，基于ANSYS仿真软件，分别改变吊挂纵向，横向，垂向刚度，研究车体弹性模态和吊挂设备刚体模态频率及振型MAC的变化，给出模态频率和振型的变化规律，为模态试验和工程计算提供参考依据。

振动与波；吊挂刚度；车体模态；吊挂模态；MAC

模态是结构的固有特性，其振型表示了在某一频率下结构各点的相对位移关系。模态频率是车辆研究的重要参数，我国《200 km/h及以上速度级铁道车辆强度设计及实验鉴定暂行规定》要求整备车体1阶弯曲自振频率应不低于10 Hz[1]；因此，要对车辆进行试验的基础上进行建模和仿真计算。

1 理论依据

1.1 模态计算

车体与地面由四个刚度相等的弹簧连接，吊挂与车体之间用四个刚度和阻尼连接。简化模型平面图如图1所示。

车体是一个连续体，可等效为欧拉伯努利梁车体。车体振动的偏微分方程为[2]

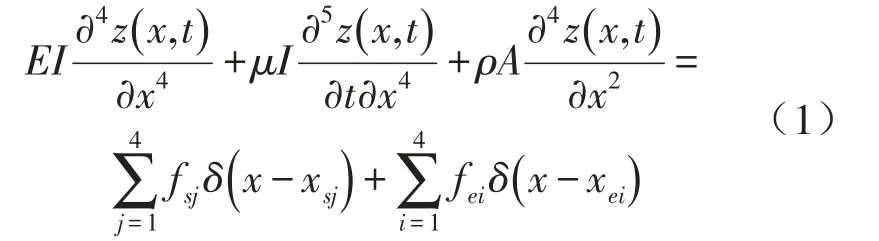
式中z(x,t) z(x,t)为车体在x坐标位移处t时刻的位移；μ为车体内滞阻尼系数；fsj为车体与地面之间连接弹簧的第j支撑点的作用力，xsj为其第j支撑位置坐标；fei为车下设备的第i悬挂点的作用力；δ为狄拉克函数；xei为车下设备第i悬挂点位置坐标。

可离散化为N个自由度，列出车体在物理坐标系统中的运动方程

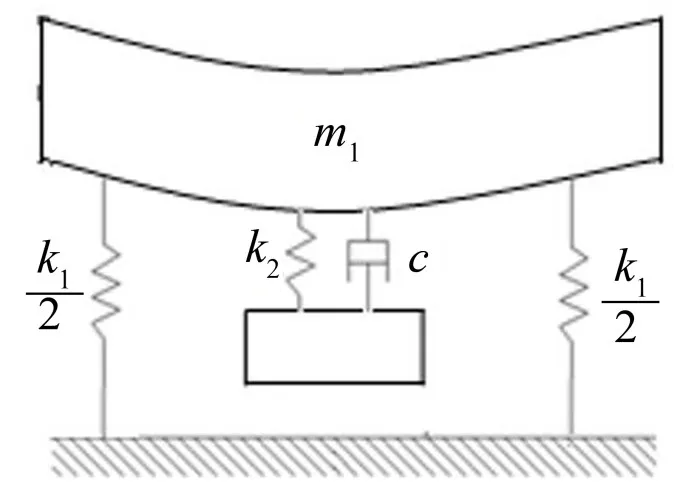
图1 简化模型图

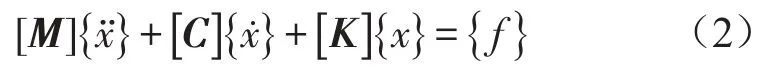
其中[M]、[C]、[K]分别是系统的质量矩阵、阻尼矩阵，刚度矩阵；{x}、{x˙}、{x¨}分别为系统各质点的位移矩阵、速度矩阵、加速度矩阵；{f}为施加外力。

系统各阶特征向量之间是关于质量阵和刚度阵正交[2]，因此可将物理坐标转换为模态坐标。令

其中φr为系统的各阶特征向量，qr为转换后的新坐标列阵。

将式（2）带入式（1）求得模态坐标下系统的运动微分方程为

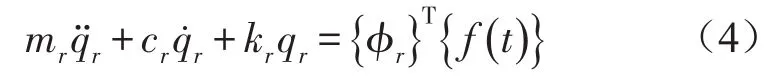
其中mr，cr，kr分别为模态质量、模态阻尼、模态刚度。令{f}={F} ejωt，qr=Qrejωt，带入式（3）得

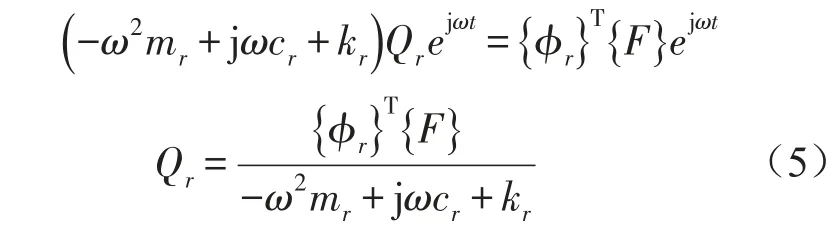
Qr相当于一个质量、刚度和阻尼分别为mr、cr、kr的单自由度系统在模态力Pr={φr}T{F}作用下的响应。

令{x}={X} ejωt，由式（3）、式（5）和qr=Qrejωt可得

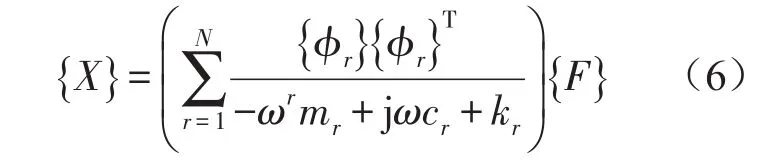
{X}为系统响应。

车下设备的运动方程为[8]

式中zc、θc分别为设备沉浮位移与侧滚活摇头位移；Ic为设备侧滚或摇头惯量。

1.2 MAC计算

模态判定准则可以比较不同组的估计振型，研究其模态的正确性。两个模态振型向量{φ}r和{φ}s之间的模态判定准则定义为

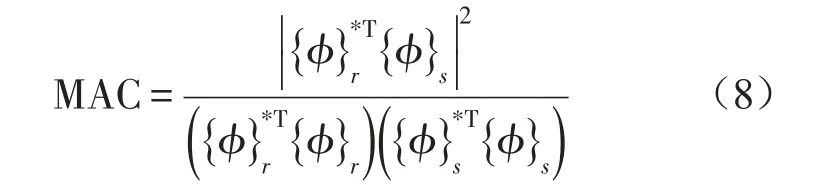
如果{φ}r和{φ}s是同一个物理模型，模态判定准则MAC应当接近于1。

计算车体振型MAC时，将车体离散为7个均匀截面，每个截面上四个点，计算吊挂MAC时，将吊挂的框架均匀离散化为20个点。

2 模型说明及计算方法

采用某型高速列车整备车体体的有限元模型，车体车下吊挂主要为变压器（模态计算时为非工作状态），车体长24.5 m，宽2.90 m，高2.45 m，悬挂点的坐标分别为（11.13，0.18，2.54），（12.15，0.18，2.54），（11.13，0.18，0.23），（12.15，0.18，0.23）。假设吊挂连接原始的纵向、横向、垂向刚度和阻尼如表1所示：

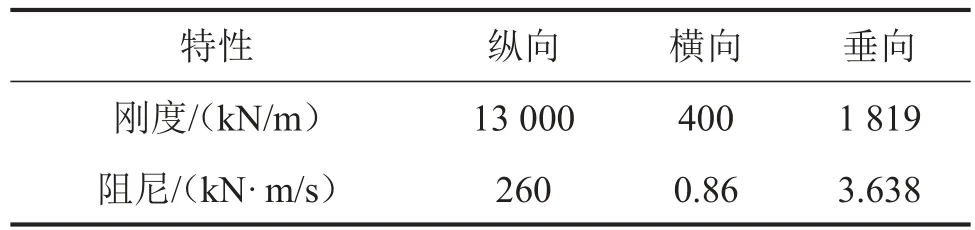
表1 各向刚度和阻尼值

分别单独改变三向刚度，并用ANSYS软件仿真计算，研究吊挂连接刚度对车体弹性模态和吊挂刚体模态的影响。

ANSYS中模态分析的方法有六种，本文主要采用分块兰索斯法，该方法采用适用于大型模型和包含形状较差的实体和壳单元的模型，可提取40阶以上模态，求解速度快，精度高，收敛性好。

3 计算结果分析

在不同吊挂刚度下，研究车体和吊挂设备模态。车体的弹性模态主要有1阶垂弯、1阶扭转、1阶菱形和1阶横弯，吊挂的刚体模态主要有1阶沉浮、1阶侧滚和1阶摇头，故为研究对象。

3.1 吊挂刚度对模态频率的影响

3.1.1 吊挂纵向刚度对模态频率的影响

吊挂不同纵向刚度下车体弹性模态和吊挂刚体模态频率及变化规律如图2所示

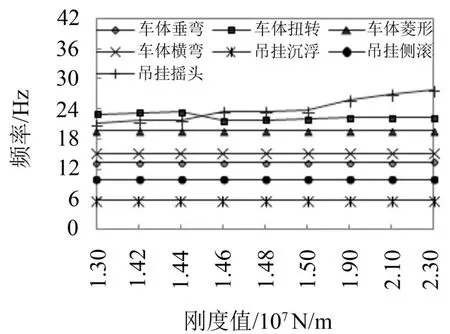
图2 车体和吊挂模态频率随纵向刚度的变化趋势

纵向刚度在一定范围内增加，1阶的车体垂弯、菱形、横弯频率和吊挂的沉浮、侧滚频率几乎不变，变化程度均小于0.1 Hz；车体的1阶扭转频率随着吊挂纵向刚度的增加先增大，后突然减小（由23.41 Hz减为21.79 Hz），吊挂的1阶摇头频率随着吊挂纵向刚度的增加而增大。

3.1.2 吊挂横向刚度对模态频率的影响

吊挂不同横向刚度下车体弹性模态和吊挂刚体模态频率及变化规律如图3所示

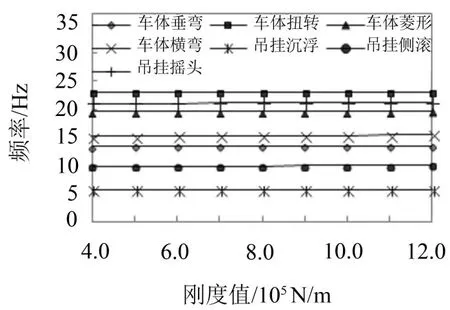
图3 车体和吊挂模态频率随横向刚度变化趋势

吊挂横向刚度一定范围内增加，车体1阶的垂弯、扭转、菱形和吊挂的沉浮、侧滚、摇头频率几乎不变，变化程度均小于0.1 Hz。车体的1阶横弯频率发生微小变化，变化程度小于1 Hz。

3.1.3 吊挂垂向刚度对模态频率的影响

吊挂不同垂向刚度下车体弹性模态和吊挂刚体模态频率如图4所示

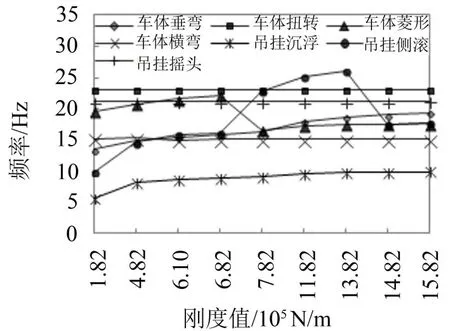
图4 车体和吊挂模态频率随垂向刚度变化趋势

吊挂垂向刚度一定范围内的加大后增加车体1阶的垂弯与吊挂的沉浮频率也隨之明显增大；车体的一阶扭转、横弯频率和吊挂的摇头频率几乎不变，变化程度均小于0.1 Hz；车体的1阶菱形频率先增大，后突然减小（由22.05 Hz减为16.58 Hz），吊挂的1阶侧滚频率先增大，又突然减小（由25.95 Hz减为17.57 Hz）。

3.2 吊挂刚度对振型的影响

吊挂纵向刚度一定范围内变化时，车体扭转和吊挂摇头频率变化较大；吊挂垂向刚度一定范围内变化时，车体菱形和吊挂侧滚频率变化较大。故其振型为主要研究对象。

3.2.1 吊挂纵向刚度对车体和吊挂振型影响

车体1阶扭转频率趋势和吊挂1阶摇头频率趋势出现交叉，即在纵向刚度增大到某一值后，二者频率发生了交换。假设二者频率趋势未交叉，称此变化趋势为原始趋势，原始趋势下的1阶扭转和1阶摇头振型为原始扭转和原始摇头，以原始刚度下车体扭转振型为参考对象，对原始扭转和原始摇头频率下的车体振型做MAC计算，得到结果如图5所示

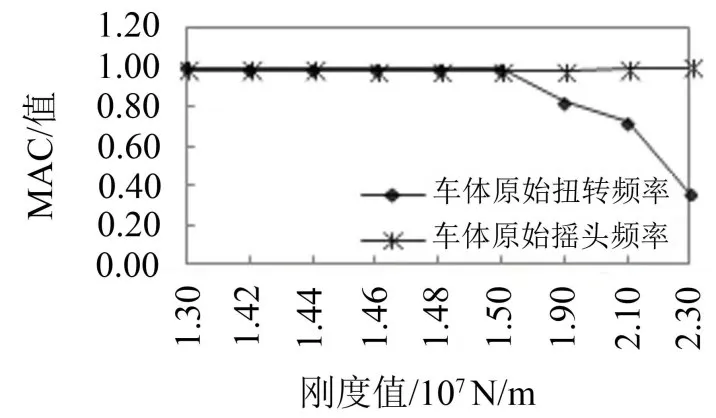
图5 原始频率下车体振型MAC随纵向刚度变化趋势

原始摇头频率下车体振型的MAC几乎都等于1；原始扭转频率下车体振型MAC值在纵向刚度大于15 000 kN/m时变小，明显小于1，即此时车体1阶扭转频率为原始摇头频率。在MAC值相同时，考虑振型的最大位移。纵向刚度小于15 000 kN/m时，计算二者频率下车体位移的最大值，结果如图6所示。

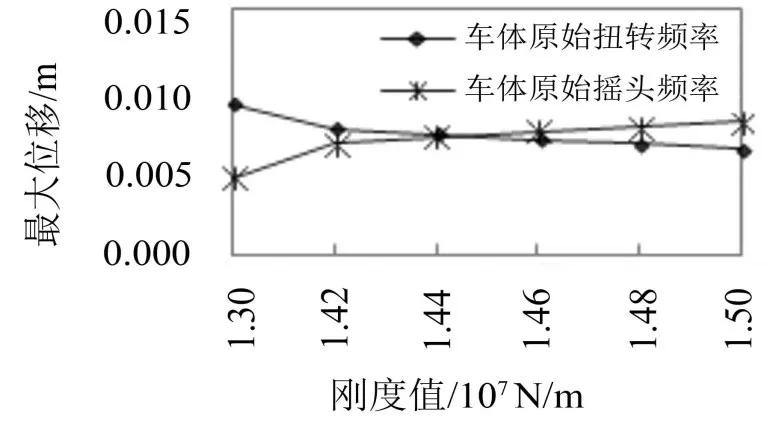
图6 原始频率下车体振型最大位移随纵向刚度变化趋势

随着纵向刚度增大，原始扭转频率下车体振型的最大位移减小，原始摇头频率下车体振型最大位移增大，二者在刚度值介于14 400 kN/m～14 600 kN/m时交叉。综合考虑车体振型MAC值和最大位移，纵向刚度值小于等于14 400 kN/m时，车体1阶扭转频率为原始扭转频率，纵向刚度值大于14 400 kN/m时，车体阶扭转频率为原始摇头频率。

同理，以原始刚度下吊挂的1阶摇头振型为参考，将吊挂离散化后计算其振型MAC和最大位移，结果如图7和图8所示。

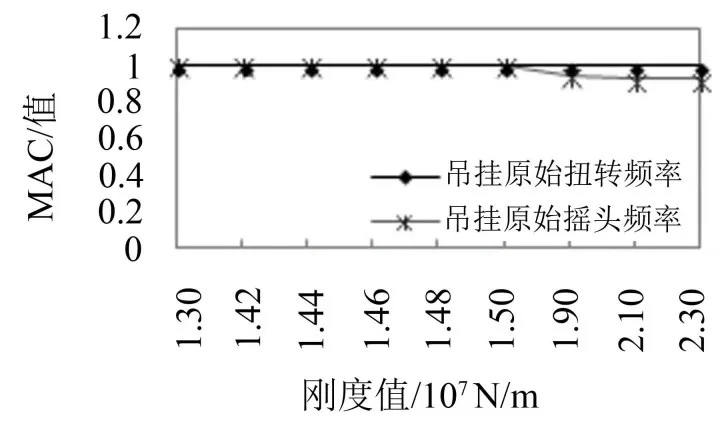
图7 原始频率下吊挂振型MAC值随纵向刚度变化趋势

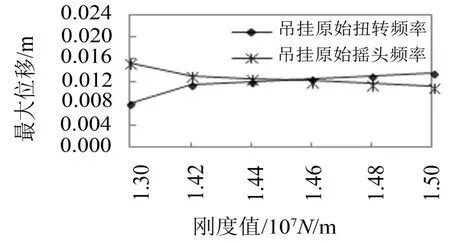
图8 原始频率下吊挂振型最大位移值随纵向刚度变化趋势

综合考虑吊挂振型的MAC值和最大位移，纵向刚度值小于等于14 400 kN/m时，吊挂1阶摇头频率为原始摇头频率，纵向刚度值大于14 400 kN/m时，吊挂1阶摇头频率为原始扭转频率。

综上所述，在纵向刚度介于14 400 kN/m～14 600 kN/m时，车体的1阶扭转频率和吊挂的1阶摇头频率发生了交换，变化趋势发生了交叉，即证明了图2模态频率变化趋势的正确性。

3.2.2 吊挂垂向刚度对车体和吊挂设备振型影响

由车体1阶菱形和吊挂1阶侧滚的频率变化趋势可知，二者频率在某一刚度值时发生了交换。假设二者频率趋势未交叉，称此变化趋势为原始趋势，原始趋势下的1阶菱形和1阶侧滚振型为原始菱形和原始侧滚，以原始刚度下车体菱形振型为参考对象，对原始菱形和原始侧滚频率下的车体振型做MAC计算，结果如图9所示。

可明显得到，随着垂向刚度的增加，原始菱形频率下车体振型MAC值逐渐减小，原始侧滚频率下车体振型MAC值逐渐增加，垂向刚度介于6 819 kN/ m～7 819 kN/m时二者交叉，即垂向刚度小于等于6 819 kN/m时，车体1阶菱形频率为原始菱形频率，垂向刚度大于6 819 kN/m时，车体1阶菱形频率为原始侧滚频率。

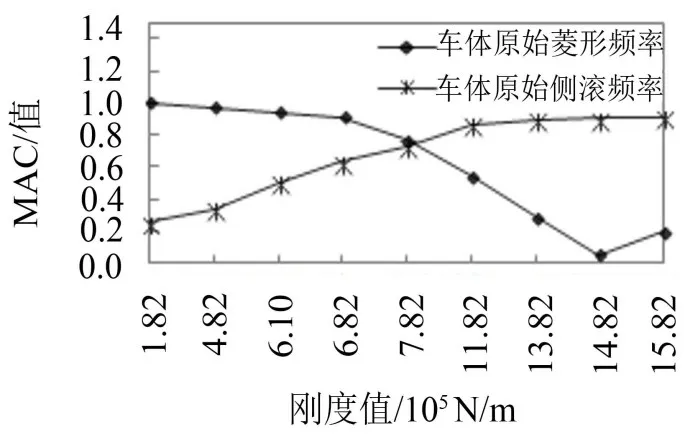
图9 原始频率下车体振型MAC值随垂向刚度变化趋势

同理，以原始刚度下吊挂侧滚振型为参考对象，对原始菱形和原始侧滚频率下吊挂振型做MAC计算，结果如图10所示。

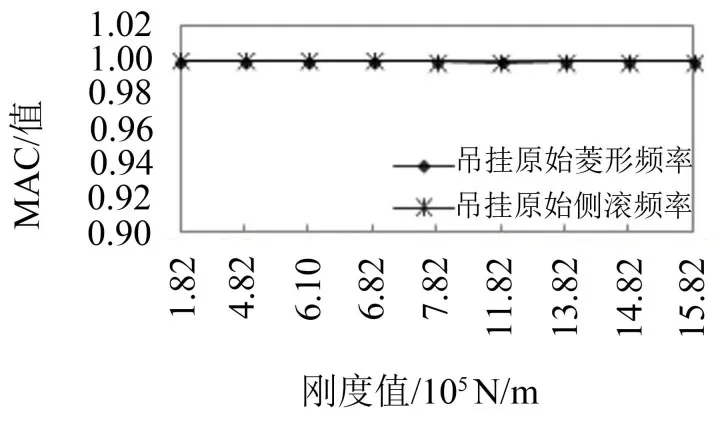
图10 原始频率下吊挂振型MAC值随垂向刚度变化趋势

随着垂向刚度的变化，原始频率下吊挂振型的MAC值几乎没有变化，都约等于1，无法区分振型，因此考虑吊挂振型的最大位移，如图11所示。

随着垂向刚度的增大，原始侧滚频率下吊挂振型最大位移逐渐减小，原始菱形频率下吊挂振型最大位移先增大后减小。刚度介于6 819 kN/m～7 819 kN/m时二者出现交叉，并且当垂向刚度大于等于14 819 kN/m时，二者差别很小。因此，垂向刚度小于等于6 819 kN/m时，吊挂1阶侧滚频率为原始侧滚频率，大于6 819 kN/m而小于14 819 kN/m时，吊挂1阶侧滚频率为原始菱形频率，大于等于14 819 kN/m时为原始侧滚频率。

由此可得，垂向刚度介于6 819 kN/m～7 819 kN/m时，车体1阶菱形频率和吊挂一阶侧滚频率发生交换，变化趋势出现交叉，并且当垂向刚度大于等于14 819 kN/m时，吊挂侧滚频率又回归于原始侧滚频率，和车体1阶菱形频率融为一体。由此可知图8模态频率变化趋势的正确性。

4 结语

（1）通过改变吊挂三个方向刚度，对车体和吊挂的模态计算，得到了车体弹性模态和吊挂刚体模态的变化规律，为工程计算及实验提供了理论参考；

（2）车体的1阶垂弯，1阶菱形频率和变压器的1阶沉浮，1阶侧滚频率主要承受吊挂垂向刚度的影响；车体的1阶横弯频率主要承受吊挂横向刚度的影响；车体的1阶扭转频率和吊挂的1阶摇头频率主要承受吊挂纵向刚度的影响；

（3）当吊挂垂向刚度达到一定值时，车体的1阶菱形频率和吊挂的1阶侧滚模态融为一体。

[1]王悦明，黄成荣，黄 强，等.200 km及以上速度级铁道车辆设计及实验鉴定暂行规定[Z].2001，9.

[2]黄彩虹，曾 京，邬平波，等.铁道客车车体弹性振动减振研究[J].工程力学.2010，21(12)：250-256.

[3]吴会超，邬平波，曾 京，等.车下设备对车体振动的影响[J].交通运输工程学报.2012，12(5)：50-56.

[4]李德葆，陆秋海.实验模态分析及其应用[M].北京：科学出版社，2011.58-63.

[5]海伦等.模态分析理论与实验[M].白化同，郭继忠译，北京：北京理工大学出版社，2001.73-75.

[6]靳晓雄，张立军，江浩.汽车振动分析[M].上海：同济大学出版社，2002.264-281.

[7]余建勇，张立民等.车体下吊吊挂设备对整备车车体模态的影响[J].噪声与振动控制，2012，(3)：97-100.

[8]吴会超，邬平波.车下设备悬挂刚度对车辆平稳性影响[J].噪声与振动控制.2012，(4)：73-77.

[9]刘堂红，江 帆.基于ANSYS的耐冲击性可车车体模态分析[J].铁道机车车辆.2002，(6)：24-27.

[10]Suzuki Y,Akutsu K.Theoretical analysis of flexural vibration of car body[J].QR of RTRI,1900,31(1):42-48.

Influence of Hanger’s Stiffness on the Modals of Vehicle’s Body and Equipments

GAO Rong-rong1,ZHANG Li-ming1,QIU Fei-li1, BAN Xi-yi1,SUN Xian-liang2

（1.State Key Lab.of Traction Power,Southwest Jiaotong University,Chengdu 610031,China; 2.CSR Sifang Locomotive and Rolling Stock Co.Ltd.,Qingdao 266111,Shandong China）

Body modals and hanging equipment modals are important characteristics of the vehicles.Their modal frequencies vary w ith the change of various factors.To obtain the elastic modals,the vehicle’s body is equivalent to an Euler Bernoulli beam.Based on the finite element model of a certain type of high speed train and ANSYS software,the variations of the elastic modals of the vehicle’s body,and the frequency and MAC of the modals of the hangers are studied under different axial,horizontal and vertical stiffness of the hangers.This work provides the basis for modal test and engineering calculation of vehicles.

vibration and wave;hanging stiffness;car body modal;hang modal;MAC

1006-1355(2014)04-0005-05

TB53；U271.91 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.002

2013-10-18

高荣荣（1989-），女，山西绛县人，硕士研究生，主要研究方向：高速列车振动研究。

张立民，男，研究员。

E-mail:zhang-lm01@163.com