无刷双馈电机模糊直接转矩控制系统的研究

，，

(洛阳供电公司，河南洛阳 471000)

0 引言

无刷双馈电机(BDFM)由串级感应电机发展而来，是一种新型的，同时具有同步电机和异步电机特点的交流调速电机。将串级联结的两台独立的定转子组合并为单一定转子绕组，并装在同一定转子铁心内，使得两种不同极数的绕组共用同一磁路，避免了滑环和碳刷，又通过改进进一步简化了定转子绕组[1]。由于其结构简单、运行可靠、变频器容量小、对电网的谐波污染少、功率因数可调等优点，对这种电机的研究越来越受到国内外学者的关注[2]。

1 无刷双馈电机的工作原理

1.1 概述

BDFM的结构示意图如图1所示。定子绕组由两套极数不同的三相绕组构成，彼此相互独立。其中一套为功率绕组，直接接工频电源；另一套为控制绕组，接变频电源。转子通常为笼型结构，通过电机转子的磁动势谐波或磁导谐波对定子不同极数的旋转磁场进行调制来实现电机的机电能量转换。其极对数为功率绕组极对数Pp和控制绕组极对数Pc之和。

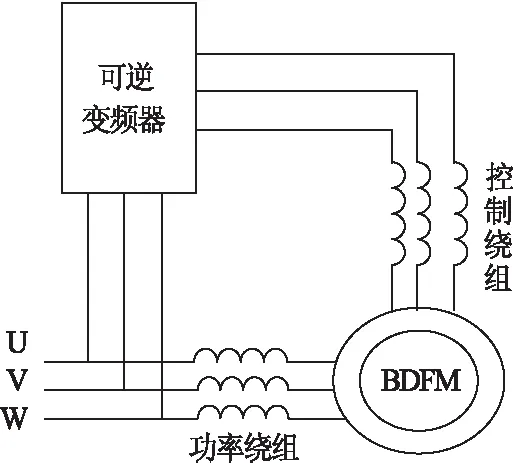
图1 BDFM结构示意图

当BDFM稳态运行时，其转速应满足

(1)

式中，nr—电机转速；fp—功率绕组频率；fc—控制绕组频率；Pp—功率绕组极对数；Pc—控制绕组极对数。

BDFM在d-q坐标轴系中的数学模型在早期的研究中已经获得[3]，其数学表达式如式(2)所示。

(2)

式中，p—微分算子；Pp、Pc—是功率绕组和控制绕组的极对数；udp、uqp、idp、iqp—是功率绕组电压和电流d、q分量；udc、uqc、idc、iqc—控制绕组电压和电流d、q分量；udr、uqr、idr、iqr—转子绕组电压和电流d、q分量；Rp、Rc、Rr—功率绕组、控制绕组及转子绕组电阻；Lsp、Lsc、Lr—功率绕组、控制绕组及转子绕组全电感；Mp、Mc—功率绕组、控制绕组与转子绕组之间的互感；ωr—转子机械角速度。

电磁转矩方程为

Te=Tep+Tec

=PpMp(iqpidr-idpiqr)+PcMc(iqcidr+idciqr)

(3)

式中，Tep、Tec—功率绕组和控制绕组产生的电磁转矩。

机械运动方程为

(4)

式中,J、TL—转子机械惯量和负载转矩。

由式(2)、式(3)、式(4)构成了BDFM在d-q坐标轴系中的数学模型，该模型简单实用[4]。

2 无刷双馈电机模糊DTC系统

2.1 概述

交流电机是一种非线性、多变量、强耦合的被控对象，模糊控制在解决交流电机的控制方面有着非常显著的优势。由于传统的DTC中磁链控制器和转矩控制器一般使用施密特触发器，控制性能受其容差大小的影响非常大，而且容差大小本身就属于模糊量，若采用模糊控制器，系统性能可以进一步得到提升[5、6]。近几十年来，国内外学者都已成功的将模糊控制应用在DTC中。本文对转矩误差、磁链误差及磁链角度进行了非常合理的模糊分级，通过模糊推理来选择适合的电压空间矢量，从而获得了比常规DTC更优越的控制性能。

2.2 模糊控制规则表

本文中，模糊控制器的输入是转矩误差eT、定子磁链误差eψ和磁链角θ，输出为逆变器的8个开关状态Sabc，因为这8种开关状态本身是准确的清晰量，所以就不需要进行模糊化。在控制器中，这8种开关状态用其所对应的十进制数来表示。在转矩误差eT的论域上定义了5个模糊子集，在定子磁链误差eψ的论域上定义了3个模糊子集，在磁链角θ的论域上定义了12个模糊子集，这更加细化了误差的大小。在模糊化过程中，对转矩误差的分档之所以比对定子磁链误差的分档更细是因为本文所遵循的原则是转矩优先，在此原则的基础上再保证定子磁链幅值恒定。我们可以得到如表1所示的模糊控制规则表[7]。

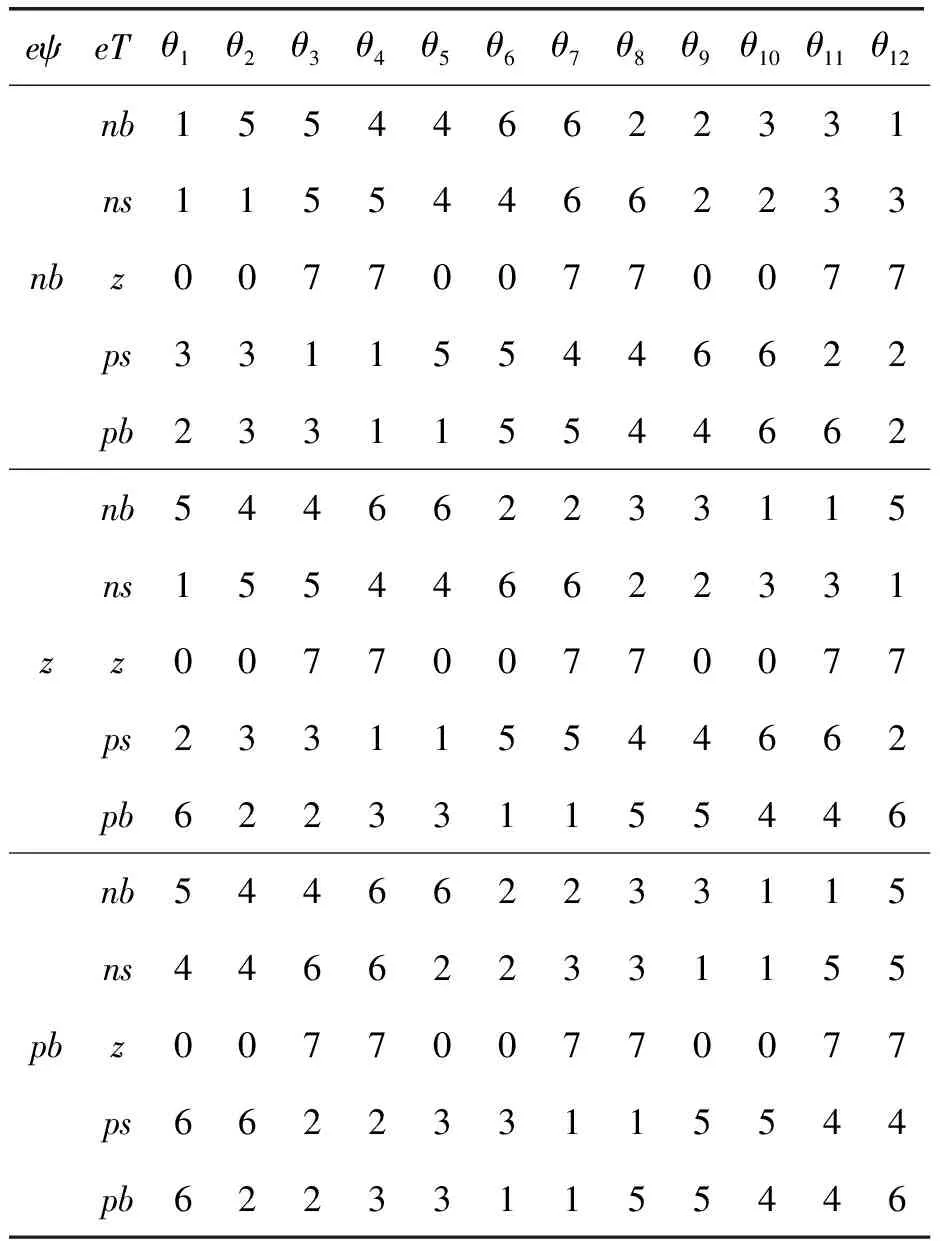
表1 模糊控制规则表

2.3 模糊DTC系统的搭建

BDFM的模糊DTC系统结构图[8]如图2所示。

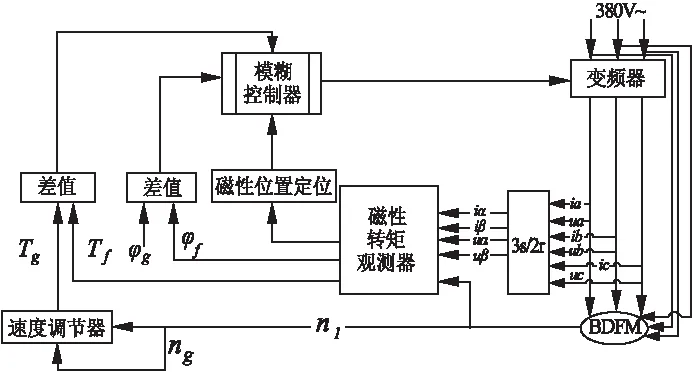
图2 BDFM模糊DTC系统结构图

3 系统仿真

本节利用Matalab/Simulink搭建BDFM动态数学模型和仿真模型。电机的仿真参数为:

Rc=1.625Ω,J=0.1kg·m2,Lsp=0.3903H,Mp=0.302H,Rp=15.3Ω;Mc=0.35,Rr=6.2Ω,Lr=0.650H;Pc=1,Lsc=0.408H。

3.1 亚同步仿真分析

如图3至图5所示分别为亚同步状态下加入模糊控制前后的转速波形、转矩波形及磁链波形。图中，在0.15s之前，电机单馈启动，给定转速为1000r/min；0.15s时，给定转速675 r/min，在0.35s时，加负载转矩4N·m。

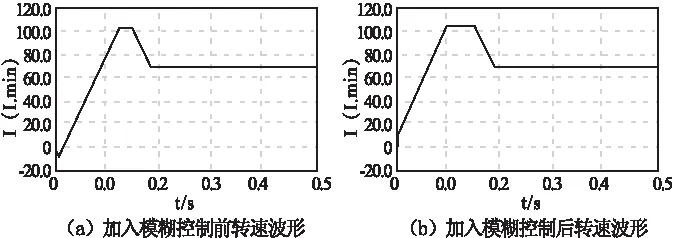
图3 亚同步状态下加入模糊控制前后的转速波形

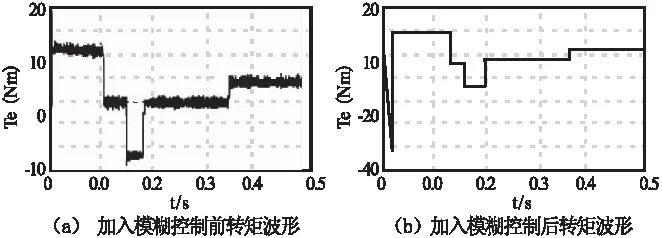
图4 亚同步状态下加入模糊控制前后的转矩波形

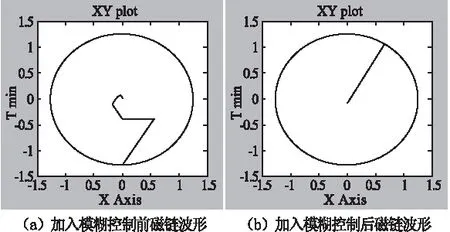
图5 亚同步状态下加入模糊控制前后的磁链波形

3.2 超同步仿真分析

如图6至图8所示分别为超同步状态下加入模糊控制前后的转速波形、转矩波形及磁链波形。图中，在0.15s之前，电机单馈启动，给定转速为1 000r/min；0.15s时，给定转速825 r/min，在0.35s时，加负载转矩4N·m。

图6超同步状态下加入模糊控制前后的转速波形

图7超同步状态下加入模糊控制前后的转矩波形

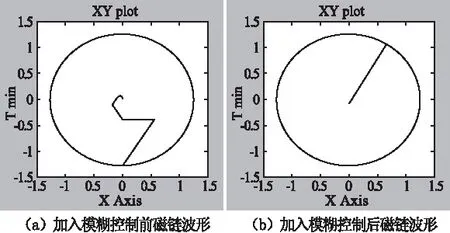
图8超同步状态下加入模糊控制前后的磁链波形

3. 3 亚同步向超同步过渡仿真分析

如图9至图11所示分别为亚同步向超同步过渡状态下加入模糊控制前后的转速波形、转矩波形及磁链波形。图中，在0.3s之前，电机单馈启动，给定转速为1 000r/min；0.3s时，给定转速675r/min，在0.6s时，给定转速825r/min，负载转矩为零。

图9亚同步向超同步过渡状态下加入模糊控制前后的转速波形

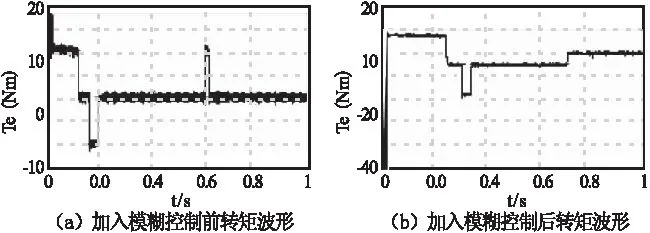
图10亚同步向超同步过渡状态下加入模糊控制前后的转矩波形

图11亚同步向超同步过渡状态下加入模糊控制前后的磁链波形

3.4 仿真结果分析

图3至图5、图6至图8、图9至图11分别给出了BDFM采用模糊DTC控制方法时，运行在亚同步、超同步及从亚同步过渡到超同步时的转速、转矩、磁链波形。从仿真的结果我们不难看出本文所设计的BDFM的模糊DTC系统是正确的，而且性能非常好，转速转矩响应速度快。本节设计的模糊控制器不但具有响应快的优点，而且转矩、转速脉动明显减小。

4 结语

本文重点阐述了模糊控制在BDFM的DTC系统中的应用。完成了依据转矩信息差值、磁链信息差值、磁链角来输出逆变器开关状态的模糊控制器的设计，在Matalab/Simulink中搭建了BDFM的模糊DTC仿真系统并进行了仿真。从仿真结果可以看出模糊直接转矩控制系统比传统直接转矩控制系统的效果要好很多，在很大程度上减小了转矩和磁链的脉动，增加了准确性。因此，模糊DTC控制是一种很有前途的控制策略，可以进一步应用到BDFM的有功无功调节等场合[9]。

[1] 胡必武,余成.无刷双馈电机的定子绕组比较研究[J].微特电机,2007,(9):10-11;61.

[2] Betz, R.E. Jovanovic, M.G. TheoreticalAnalysisofControlPorpertiesfortheBusrhless Doubly-Fed Reluctance Machine. Energy Conversion IEEE Transactions,2002,17(3):332-33

[3]A. K.Wa11ace, P.Rochelle，R.Spee. Rotor modeling and development for brushless doubly-fed machines.Electirc Machines and Power Systems,1995,23:703-715.

[4] Li Ruqi, Wallace A. Tow-axis model development of cage-rotorbrushless doubly-fed motors[J]. IEEE Transon EnergyConversion(S0885-8969),1991, EC-6(3): 453-460.

[5] 窦曰轩,王洪艳.模糊直接转矩控制系统Matlab/Simulink仿真[J].计算机仿真，2001,15(2):70-72.

[6] 冉振亚,杨超,曹文明.基于Matlab/Simulink的电动汽车驱动系统启动过程的模糊控制与仿真[J].客车技术与研究,2004,26(4):1-3.

[7] 焦卫星.基于模糊理论的无刷双馈电机直接转矩控制系统研究[D].广州:华南理工大学,2012.

[8] 吴聂根. DTC在无刷双馈风力发电系统中应用的研究[D].广州:华南理工大学,2010.

[9] 赵辉,彭涛,岳有军,等.模糊自适应PID控制在无刷双馈电机矢量控制中的应用[J].天津理工大学学报，2008,24(3):36-39.