改进遗传算法在PMSM矢量控制系统优化设计中的应用
2014-08-30,,,
,,,
(湖南科技大学,湖南湘潭 411201)
0 引言
永磁同步电机(PMSM)因为具有结构简单、功率因素和功率高、稳定、可靠性高等优点,而被广泛应用于工业交流伺服系统,如各类自动化装配设备和机器人等[1]。因此,对PMSM的控制研究就成了比较热门的课题,为了使PMSM具有更广的调速范围、更小的转矩脉冲及更快的动态响应性能,矢量控制方法与其他控制策略相比具有很大的优势,因为矢量控制法可以通过Clark和Park变换使PMSM具有直流电机一样的调速性能。但是在一般的矢量控制系统中常会涉及到三个PI控制器,而这三个PI控制器的参数则会直接影响到系统的性能,为了找出这三个PI控制器的最优参数,通常可以把该问题看成是对一个有多变量、非线性、多峰值、多性能指标的目标函数进行求解的问题,针对此问题,若采用遗传算法对目标函数求解会有很大的优势,但是普通的遗传算法对PI参数寻优常会存在全局收敛性与收敛速度之间的矛盾[2]。因此,本文在普通遗传算法的基础上采用一种新的变异操作和交叉操作,通过仿真实验,验证了该改进遗传算法能有效的解决全局收敛性与收敛速度之间的矛盾。
1 PMSM调速系统的矢量控制
1971年,德国学者F.Blaschke提出了矢量控制理论[3],矢量控制亦称磁场定向控制(FOC),从理论上阐述,它将电机电流分解为相互垂直且彼此独立的两个分量,转矩电流分量和定子电流分量,然后分别对这两个量进行控制,这样PMSM的转矩控制原理就与直流电机相似,从而使得PMSM具有良好的动态特性,图1为PMSMid=0控制原理图。
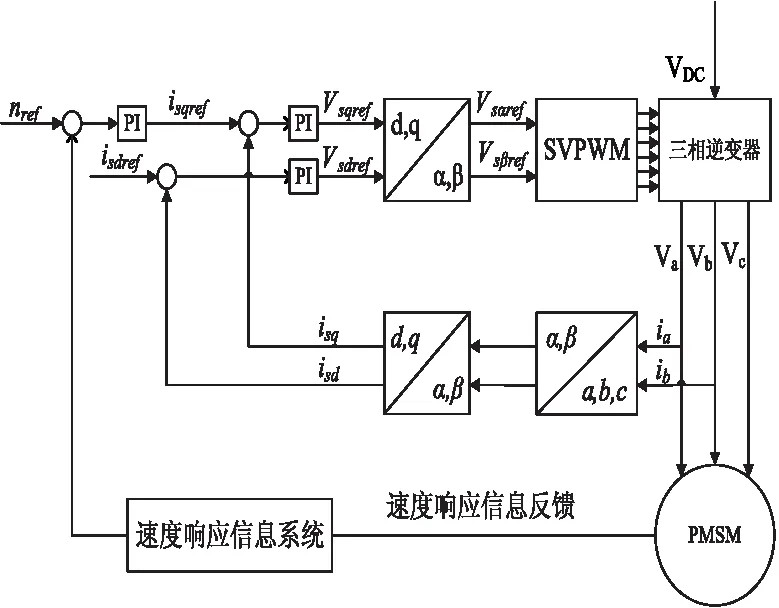
图1 PMSM id=0控制原理图
具体的控制原理为:目标转速nref与速度响应系统反馈转速的差值经过速度调节器调解得到转矩电流的给定值iSqref,转矩电流的给定值与检测到的实际的转矩电流iSq的差值以及id的期望值0与检测到的实际d轴电流iSq,由两个电流调节器调解得到合适的q轴和d轴电压值VSqref、VSdref。通过两相/两相旋转变换(2s/2r变换)得到VSαref、VSβref,最后通过SPWM方法计算得到6路脉冲驱动电机。从原理可知,在永磁同步电机调速系统中3个PI控制器的参数选择将直接影响到系统的性能。
2 改进遗传算法
从矢量控制原理分析可知PID参数是一个多参数组合优化的问题。遗传算法作为一种模拟生物界自然选择和遗传机制的随机化搜索算法,在可并行处理得到全局最优解方面,具有很大的优势[4~6]。然而实践表明,普通遗传算法在大规模多目标寻优时总会存在早熟收敛及收敛速度慢的现象。为此,本文引入在交叉概率及变异概率方面进行改进的遗传算法,以消除早熟收敛及收敛速度慢的情况。
2.1 目标函数
在目标函数的选取上,由于系统的静差、超调量、建立时间及上升时间都是作为评价一个系统性能的指标。因此本文把上述性能指标进行加权,从而得到响应的评价函数
J=B×α+Tr×β+O×η+Ts×λ+Ess×μ
(1)
(2)
ωe(k)=ωr(k)-ωf(k)
(3)
式中,B—综合绝对误差;Tr—上升时间;O—超调量;Ts—建立时间;ESS—静差;α,β,η,λ,μ—各指标的权重;ωe(k)—第k次采样转度误差;ωr(k)—第k次采样转速给定值;ωf(k)—第k次采样转度反馈值。
通常对于PMSM的控制性能,我们要求静差、超调量、建立时间及上升时间这些性能指标能越小越好。因此,对系统的优化,我们可以把它表示为求函数J的最小值,即
minJ
Subject toKmin≤K≤Kmax
(4)
式中,K—控制参数向量;Kmin—控制参数向量的最小值;Kmax—控制参数向量的最大值。
2.2 交叉概率与变异概率
设计交叉概率时,综合考虑了交叉算子与群体多样性的关系及交叉算子对模式的生成与破坏能力,通常希望交叉概率能够逐渐减小,直到稳定,并且针对每一个个体在同一个进化过程中能有相同的概率,因此,本文采取的交叉概率计算公式为
(5)
mtmp=Pc,max×2(-t/TGen)
(6)
式中,TGen—预设的最大进化代数,t—当前进化代数;Pc,max—预设的最大交叉概率;Pc,min—预设的最小交叉概率;Pc(t)—该种群第t代的交叉概率。该式使交叉概率与个体适应度值及遗传进化代数无关。
与交叉概率一样,在变异概率的设计问题上,我们也希望变异概率能逐渐减小直到稳定。同时,若在遗传算法进化过程中采用概率可变的变异算子,可以有效地提高遗传操作性能,如部分优秀的个体应对应相对小的变异概率,而其他劣质的个体则应对应相对大的变异概率。因此,本文采取自适应变异概率,使之随进化代数及个体适应度值的变化而变化,变异概率计算公式如下。
(7)
Pm,max
(8)
式中,fmax—该种群中最大适应度值;Pm,max—预设的最大变异概率;Pm,min—预设的最小变异概率;f(Xi)—待变异个体的适应度值;Pm(t)—该种群第t代个体Xi的变异概率。
3 仿真及分析
为了验证改进遗传算法的性能,选取普通遗传算法与本文的改进遗传算法比较。图2为改进遗传算法与普通遗传算法目标函数的收敛曲线;图3为速度响应曲线。

图2 目标函数的收敛曲线

图3 速度响应曲线
由图2可知本文的改进遗传算法与普通遗传算法相比较,能够在更短的时间内寻找到较优的目标值。从图3的速度响应曲线可以看出,由改进遗传算法整定PI控制器的控制系统,具有基本无超调、无静差、上升速度快且达到稳定速度所需时间短等性能,因此,改进遗传算法应用于矢量控制系统时,相比较于普通遗传算法,在全局优化性能和收敛速度方面都有较大的提高。
4 结语
从交叉概率,变异概率方面进行改进的遗传算法无论是在收敛速度还是全局优化性能方面都有了很大的提高,解决了普通遗传算法存在的全局优化性能与收敛速度之间的矛盾。将此改进遗传算法用于永磁同步电机矢量控制系统化设计中,可以找到具有无静差、响应快、无超调的控制参数,从而使永磁同步电机的性能得到进一步的提升。
[1] Caponio A,G L Cascella.A Fast Adaptive Memetic Algorithm for Online and Offline Control Design of PMSM Drives[J].IEEE Transactions on Systems,Man,and Cybernetics,2007,37 (1) : 28-41.
[2] Gambardella L.M.; Mastrolilli M,Rizzoli A.E,Zaffalon M.An optimization methodology for intermodal terminal management[J].Journal of Intelligent Manufacturing,2001,12 (5):521-534.
[3] Zhuang M,Atherton D P.Automatic Tuning of Optimum PID Controllers[J].Control Theory and Applications,1993,140(3) :216-224.
[4] Jan R M,C S Tseng.Robust PID Control Design for Permanent Magnet Synchronous Motor:A Genetic Approach[J].Electric Power Systems Research,2008,78( 7) :1161-1168.
[5] R A Krohling,J P Rey.Design of Optimal Disturbance Rejection PID Controllers Using Genetic Algorithm[J].IEEE Trans.Evol.Comput.,2001,5: 78-82.
[6] Y Mitsukura,T Yamamoto,M Kaneda.A Design of Self-tuning PID Controllers Using a Genetic Algorithm[C].in Proc.Amer.Contr.Conf.,1999:1361-1365.
[7] 徐峰,李东海,薛亚丽.基于ITAE指标的PID参数整定方法比较研究[J].中国电机工程学报,2003,23(8).
[8] 曾进,任庆生.基于改进遗传算法的时间最优控制问题求解[J].控制与决策,2002(l).
[9] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[10] 王堔,王仕成.基于遗传算法的PID参数整定及仿真[J].计算机仿真,2005,22(10).
[11] 杨智,朱海锋,黄以华.PID控制器设计与参数整定方法综述[J].北工自动化及仪表,2005,32(5):l-7.
