肋骨刚度对环肋圆柱壳屈曲载荷的影响分析

白 旭，李金华，王晓天

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)(2.山东省科学院 海洋仪器仪表研究所，山东 青岛 266001)(3.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

肋骨刚度对环肋圆柱壳屈曲载荷的影响分析

白 旭1，李金华2，王晓天3

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)(2.山东省科学院 海洋仪器仪表研究所，山东 青岛 266001)(3.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

在推导环肋圆柱壳屈曲临界载荷的基础上，通过能量与结构刚度之间的关系,分析了肋骨弯曲刚度、扭转刚度和压缩刚度对环肋圆柱壳失稳载荷的影响.分别折减肋骨弯曲刚度和壳板刚度，研究了不同位置的肋骨在环肋圆柱壳总体稳定性中的作用，并将单根肋骨刚度折减系数转换成所有肋骨的平均折减系数；分析了壳板刚度对环肋圆柱壳总体稳定性的影响，给出了肋骨和壳板刚度同时折减时环肋圆柱壳总体稳定性的计算方法.为环肋圆柱壳的设计以及含缺陷圆柱壳承载能力的研究提供了一种理论参考.

静水压力；环肋圆柱壳；屈曲载荷；肋骨刚度；折减刚度法

薄壁环肋圆柱壳结构在船舶与海洋工程领域有着广泛的应用，多年来人们针对圆柱壳屈曲问题进行了大量的理论与试验研究，来试图解释环肋圆柱壳屈曲载荷的理论值与试验值之间的差距[1].目前除了线性和非线性理论方法以及数值计算方法来研究圆柱壳的屈曲问题外，提出了RSM(Reduced Stiffness Method)法来研究圆柱壳的屈曲下限问题，在一定程度上理论值可以与试验值很好的吻合，并将此种方法运用到复合材料圆柱壳的屈曲研究[2-5].2007年美国NASA 开展了SBKF(Shell Buckling Knockdown Factor)项目，此项目的目标是建立一种相对不保守的实用的壳体屈曲设计和分析技术来降低环肋圆柱壳结构的重量[6-8].文献[9]通过“能力减弱系数”修正线弹性方法来求得的壳体临界屈曲载荷值，为壳体结构屈曲研究提供了一种新的方法.

针对静水压力载荷作用下的环肋圆柱壳结构，通过折减肋骨刚度和壳板刚度，研究了肋骨各部分刚度以及不同位置的肋骨对环肋圆柱壳稳定性的影响，并给出了同时折减肋骨和壳板刚度时环肋圆柱壳稳定性的计算方法.为环肋圆柱壳的设计和含缺陷圆柱壳承载能力研究提供一种新的思路.

1 环肋圆柱壳屈曲载荷

承受静水压力载荷的环肋圆柱壳结构如图1所示，总长度为L0，肋骨间距为l，壳体壁厚为t，半径为r，外部静水压力载荷为p，材料的弹性模量为E.由文献[4]可知，控制圆柱壳稳定平衡状态的表达式如式(1).

(1)

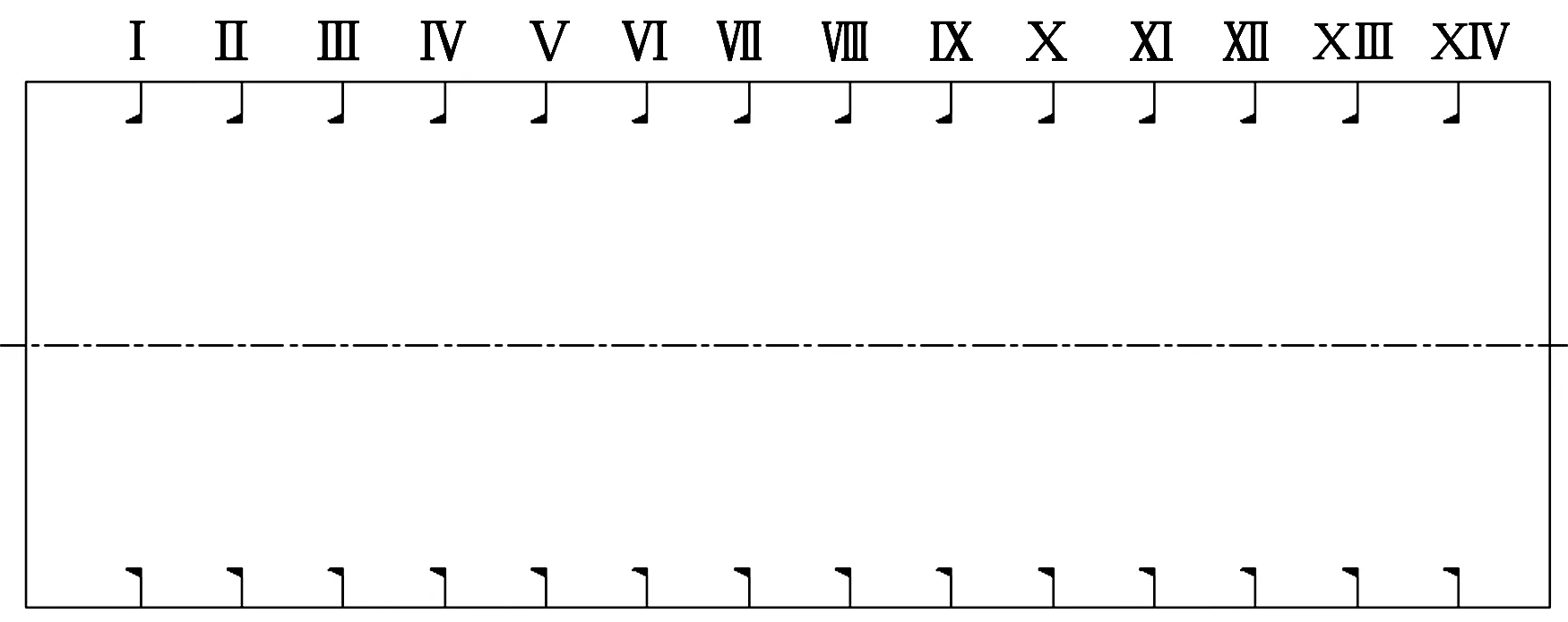
图1环肋圆柱壳示意

Fig.1Schematicdiagramofstiffenedcylindricalshell

Donnell给出的近似的圆柱壳几何方程：

(2)

式中：(u,v,w)为屈曲后的位移.

由胡克定律，则相应的应力和弯矩为

(3)

式中：K=Et/(1-μ2)，D=Et3/12(1-μ2)；n′θ和m′θ为肋骨的应力和弯矩；αr=ES/K，βr=EI/D，εr=εθ-zrγ′θ；βθr=6Ir/t3；S为肋骨横截面积；zr为肋骨的中性轴与壳板的距离；I为计及壳板的肋骨弯曲惯性矩；Ir为肋骨扭转惯性矩.

将屈曲前圆柱壳的轴向和周向应力近似取为

(4)

将式(2～4)代入式(1)即可求得确定圆柱壳稳定平衡的表达式.

环肋圆柱壳丧失总体稳定性时，壳的两端可以认为是自由支持在刚性支座上，因此失稳时的位移函数可以取为：

(5)

式中：L0为圆柱壳的总长度；i为圆周方向的波数，j为轴向方向的半波数.uij，vij，wij为任意常数.

根据壳体稳定条件，对于任意的位移增量(u,v,w)，总势能保持不变，即

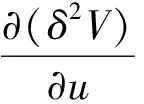
(6)

将式(5)代入式(6)得

(7)

(8)

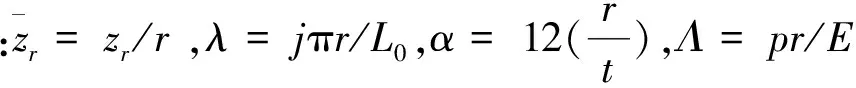
因此将环肋圆柱壳的屈曲问题转化为广义特征值问题.令式(7)的系数行列式为0，即可求得静水压力下环肋圆柱壳的总体失稳载荷.

采用以下参数:圆柱壳长L0=9200mm，肋骨间距l=450mm，圆柱壳半径(内径)r=875mm，圆柱壳板厚度t=24 mm，肋骨型号为18a球扁钢.比较各种规范和文中环肋圆柱壳公式的计算结果如表1所示.

表1 各计算公式结果比较Table 1 Results comparison of different formulas

从表1中可以看出，用文中计算静水压力下环肋圆柱壳总体失稳临界载荷的方法所得到的计算结果均低于现有规范和计算方法所得到的理论结果，但现有规范均需对理论结果进行修正.例如，针对以上参数，CCS规范修正后的结果为20.233Mpa，ABS修正后的结果为30.604 Mpa，说明文中的计算结果是可靠的.

结构刚度矩阵与应变能之间的关系为：

U=ΦTKΦ

(9)

式中：U为能量项；Φ为失稳模态；K为刚度矩阵.

由式(9)可知，圆柱壳的各部分刚度对稳定性的影响可以通过分析各部分能量在圆柱壳稳定性中的作用来实现，圆柱壳各部分刚度的折减相当于相应部分能量的损失.由于制造工艺的限制，环肋圆柱壳的尺寸偏差和形状偏差是引起刚度折减的主要原因，因此其刚度折减系数可定义为：

κ=κsize·κshape

(10)

式中：κ为圆柱壳结构的刚度折减系数；κsize为由于尺寸偏差引起的刚度折减系数，κsize=实际尺寸肋骨刚度/设计尺寸的肋骨刚度；κshape为由于形状偏差引起的刚度折减系数，与实际肋骨初始缺陷形式有关.

图2给出了肋骨各个刚度对圆柱壳总体失稳临界压力Pcr的影响曲线(所有刚度均进行了无量纲处理)，从图中可以看出，肋骨的弯曲刚度折减系数κbs对临界载荷的影响最大，随着弯曲刚度的增加，圆柱壳的总体失稳临界压力迅速增加；扭转刚度折减系数κrs对圆柱壳的总体失稳临界压力影响不大，当扭转刚度增加一个数量级时，圆柱壳总体失稳临界压力只增加0.3Mpa，因此忽略肋骨扭转刚度对圆柱壳总体失稳压力的计算结果影响不大；而压缩刚度折减系数κcs对圆柱壳总体失稳压力起负作用，随着压缩刚度的增加圆柱壳总体失稳压力有所下降，因此设计肋骨时，可以将肋骨设计成“细高”的形式.对于L0=9000，l=600，r=2500，t=25，肋骨型号为20a球扁钢的环肋圆柱壳，仅考虑弯曲刚度，其总体失稳载荷为8.4 Mpa，考虑了肋骨扭转刚度，其总体失稳载荷增加为8.6Mpa，考虑肋骨弯曲，压缩和扭转刚度后，其总体失稳载荷为8.67Mpa，由此可见，肋骨弯曲刚度在环肋圆柱壳总体失稳中起着重要作用，肋骨的扭转刚度和压缩刚度对总体失稳载荷的影响较小，可忽略不计.

图2肋骨各刚度对临界载荷的影响

Fig.2Effectsofdifferentribstiffnessoncriticalbucklingloads

2 折减肋骨刚度

通过前面的分析可知，肋骨对静水压力下环肋圆柱壳总体稳定性起着重要的作用，尤其是肋骨的弯曲刚度，对环肋圆柱壳总体失稳压力具有较大的影响.但是肋骨无论是在制造还是安装的过程中都将会由于工艺的限制存在着各种缺陷，造成实际承载能力远低于理论预测值.文中认为初始缺陷的存在影响了肋骨的弯曲刚度，不同初始缺陷对肋骨弯曲刚度的影响不同，从而造成试验数据的差异性.因此肋骨的初始缺陷对环肋圆柱壳总体稳定性的影响可以通过折减肋骨刚度的方法实现.

利用肋骨弯曲刚度折减系数κbs来研究肋骨刚度折减与临界载荷的关系.因此只需将式(8)中由肋骨弯曲应变能引起的刚度项乘以折减系数κ，则其中的相关项变为：

(11)

应用式(11)中的系数即可求得不同肋骨弯曲刚度折减系数下的临界载荷值.

图3 肋骨刚度折减系数与临界载荷的关系Fig.3 Reletionsihp of reduced coefficient of ribstiffness and critical loads

计算时取环肋圆柱壳的参数为：L0=9000，l=600，r=2500，t=25，肋骨型号为20a球扁钢，则折减系数κ与屈曲载荷之间的关系如图3所示.从图3中可以看出，静水压力下环肋圆柱壳的总体失稳载荷随着肋骨刚度折减系数κ的减小而下降，当κ接近于0时由于失稳模态的改变而迅速收敛于无肋骨时圆柱壳失稳载荷.也就是说肋骨弯曲折减系数κ涵盖了所有环肋圆柱壳可能的总体失稳值，因此可把肋骨的初始缺陷折合成肋骨弯曲刚度折减系数来研究环肋圆柱壳的总体稳定性问题.

以上研究是假设每根肋骨具有相同的初始缺陷水平而对肋骨弯曲刚度进行折减的，也就是说每根肋骨具有相同的折减系数，而实际建造中是不可能的.因此，研究每根肋骨的折减系数κn对环肋圆柱壳静水压力下总体失稳临界压力的影响.为了说明每根肋骨对环肋圆柱壳总体失稳压力的影响，忽略肋骨扭转刚度的影响，肋骨总弯曲应变能应写为：

(12)

则式(11)变为

(13)

用式(13)替换式(8)相应的系数，则可得到计算单根肋骨对环肋圆柱壳总体屈曲载荷影响的公式.仍以前面的环肋圆柱壳参数为例，而肋骨的编号如图1所示.

图4给出了折减单根肋骨弯曲刚度系数对圆柱壳总体稳定性的影响，由于肋骨的位置对称，因此只计算了一半肋骨的肋骨弯曲刚度折减系数对总体稳定性的影响.从图中可以看出，每根肋骨对圆柱壳在总体失稳时的影响是不同的，离圆柱壳长度的中点越近的肋骨对其稳定性影响越大.因此在设计环肋圆柱壳肋骨时，在保证重量不变的前提下，可适当增加圆柱壳中间附近肋骨的刚度而降低边缘位置肋骨的刚度来提高环肋圆柱壳的总体稳定性.

图4单根肋骨弯曲刚度折减系数与临界载荷的关系

Fig.4Reletionshipofreducedcoefficientofsingleribstiffnessandcriticalbucklingloads

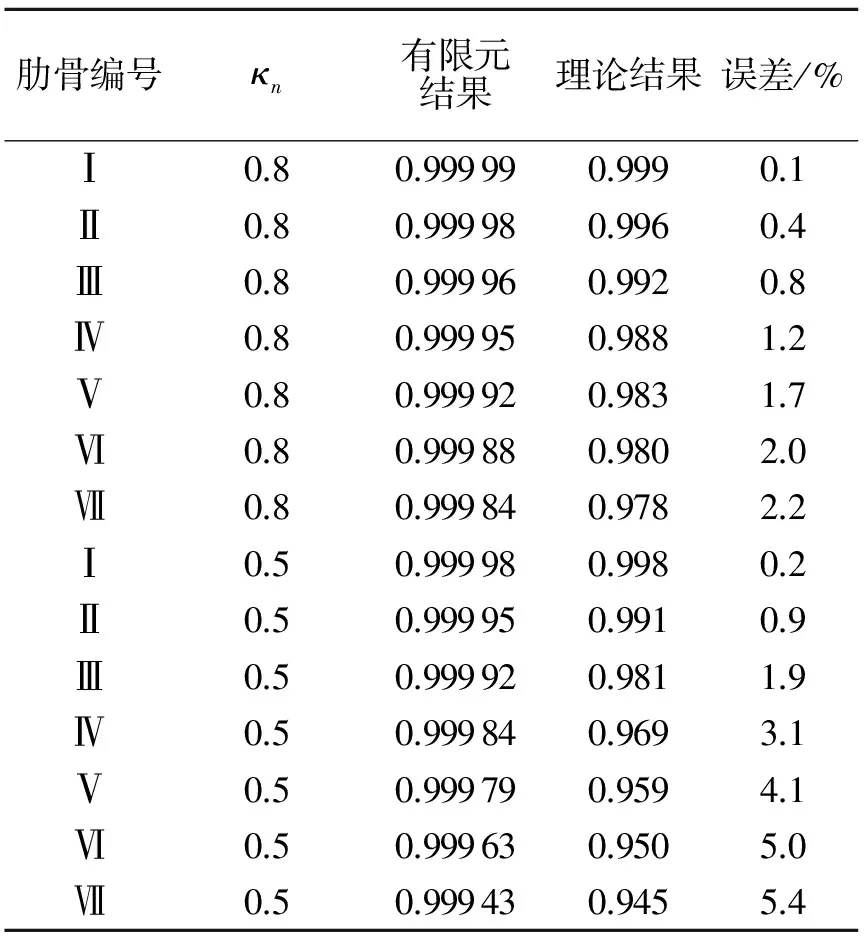
表2 理论结果与有限元结果的比较Table 2 Compared with finite element and therical results

当多根肋骨具有不同弯曲刚度折减系数时，为简化计算步骤，可以把单根肋骨的折减系数κn转换成所有肋骨的平均折减系数κ，这样应用式(11)中的系数即可计算每根肋骨具有不同折减系数时的环肋圆柱壳的屈曲载荷，其转换关系可由公式(14)确定.

(14)

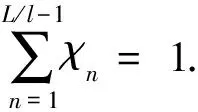
由于单根肋骨弯曲折减系数与临界载荷是线性关系，因此

(15)

对于图1所示的环肋圆柱壳，每根肋骨的权重如图5所示.

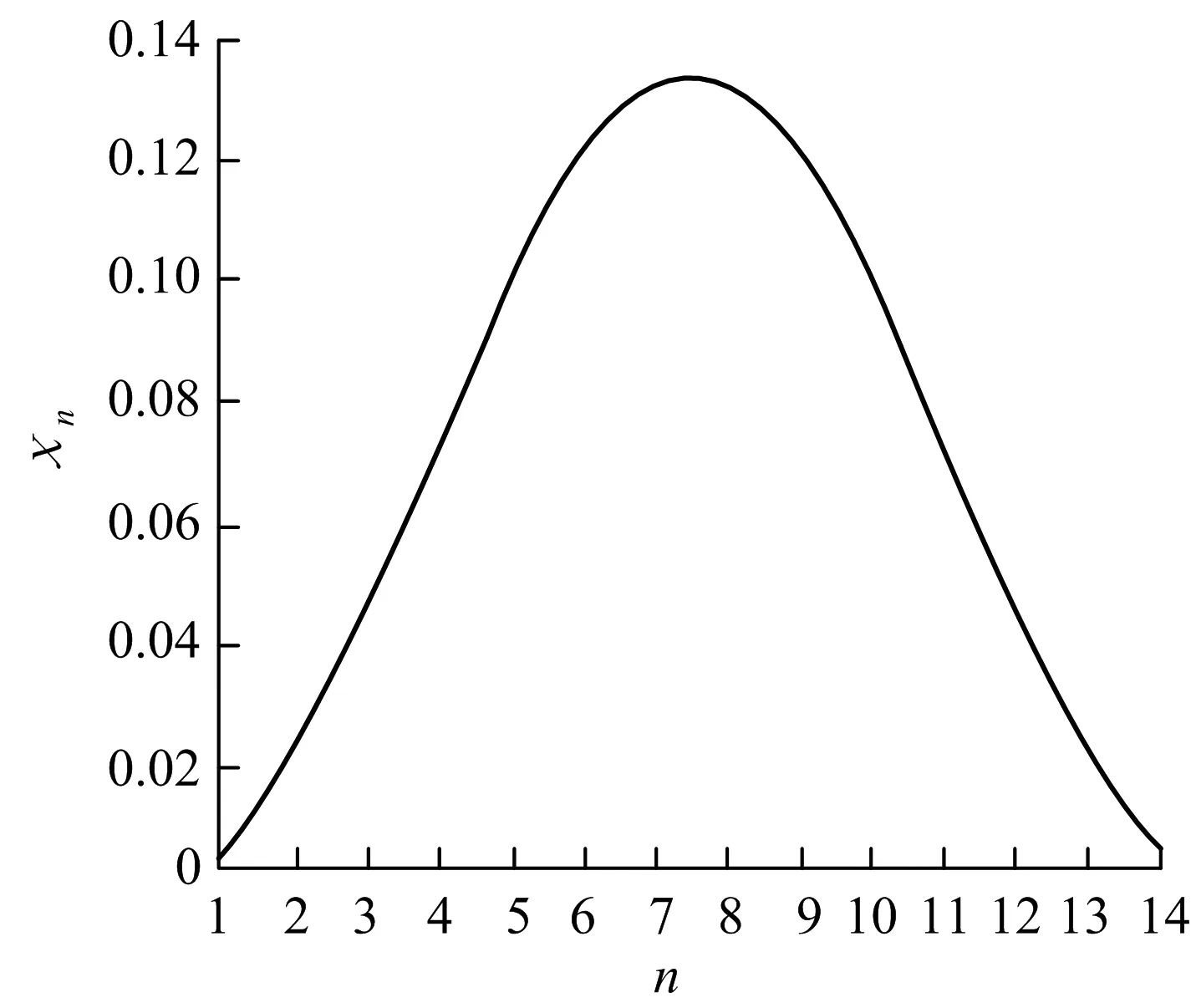
图5每根肋骨的权重

Fig.5Weightofeverysinglerib

3 折减壳板刚度

前面已经论述了肋骨对环肋圆柱壳稳定性的影响，现在考虑静水压力下环肋圆柱壳壳板薄膜刚度折减系数β与总体失稳载荷的关系.为此，应将式(8)中与壳板薄膜刚度相关的项乘以折减系数β，变为

(16)

应用(16)式中的系数即可求得壳板薄膜刚度折减系数与总体失稳载荷之间的关系.下面仍以上节中算例的参数，给出薄膜刚度折减系数与总体失稳载荷之间的关系.

图6给出了壳板薄膜刚度折减系数β与环肋圆柱壳总体失稳载荷的关系，可以看出:临界载荷随着β的减小而减小，β越小，临界载荷下降的速度就越快.当β=0时，临界载荷为无缺陷时临界载荷的71%，下降29%.因此可以说明壳板对环肋圆柱壳的总体稳定性的贡献要小于肋骨的贡献.

图6 壳板刚度折减系数与临界载荷的关系Fig.6 Reletionship of reduced coefficient ofshell stiffness and critical loads

真实的环肋圆柱壳无论是壳板还是肋骨都不可避免的同时存在着各种缺陷，使壳板和肋骨的刚度同时的降低.

图7给出了壳板薄膜刚度和肋骨弯曲刚度K同时折减时临界载荷的变化规律，从图中可以看出，3条曲线随β具有相同的变化趋势,且在β一定的情况下相邻两条曲线的差值几乎相等，因此可以认为壳板和肋骨同时存在缺陷时，可以分别计算壳板和肋骨单独存在缺陷时的临界载荷降低值,然后再相加即为两种缺陷共同作用时临界载荷的降低值，与同时计算两种缺陷时的临界载荷所产生的误差是可以忽略不计的.

图7壳板和肋骨刚度同时折减时的临界载荷的关系

Fig.7Reletionshipofcriticalloadsofreducingshellstiffnessandribstiffness

4 结论

1)不同位置肋骨对圆柱壳的影响不同，设计时可考虑适当增加中间肋骨刚度，减小边缘肋骨刚度来提高环肋圆柱壳的总体稳定性.

2)当圆柱壳同时折减肋骨刚度和壳板刚度时，可分别计算壳板和肋骨刚度单独存在时的临界载荷降低值然后再相加即为两种刚度同时折减时临界载荷的降低值.

3)环肋圆柱壳几何非线性对其稳定承载能力的影响可以归结为对环肋圆柱壳壳板刚度和肋骨刚度的影响.含初始缺陷圆柱壳的刚度折减系数，可通过建立含初始缺陷圆柱壳的几何方程，进而得到圆柱壳的总势能.通过圆柱壳的稳定条件，可得含不同形式初始缺陷圆柱壳的刚度折减系数，因此可以研究初始缺陷与环肋圆柱壳各刚度之间的关系来探讨环肋圆柱壳的稳定承载能力，这为含缺陷圆柱壳稳定性的研究提供了一个新的思路.

References)

[1] Teng Jinguang.Buckling of thin shells: Recent advances and trends [J].ApplMechRev,1996, 49(4):263-274.

[2] Croll J G A,Gavrilenko G D. Reduced-stiffness method in the theory of buckling of stiffened shells[J].StrengthofMaterial,2000, 32(2):168-177.

[3] Croll J G A.Stability in shells [J].NonlinearDynamics, 2006, 43:17-28.

[4] Jaca R C,Godoy L A,Flores F G,et al. A reduced stiffness approach for the buckling of open cylindrical tanks under wind loads [J].Thin-walledStructures,2007, 45: 727-736.

[5] Jaca R C,Godoy L A,Croll J G A.Reduced stiffness buckling analysis of aboveground storage tanks with thickness changes [J].AdvancesinStructuralEngineering.2011, 14(3):475-487.

[6] Hilburger M W.Shell buckling knockdown factor 1st annual workshop[G].USA:NASA Langley Research Center,2009.

[7] Hrinda G A. Effects of shell-buckling knockdown factors in large cylindrical shells[G].USA:NASA Langley Research Center, 2012.

[8] Hilburger M W. Developing the next generation shell buckling design factors and technologies[G].USA:NASA Langley Research Center,2012.

[9] 黄庆，赵飞云，姚伟达. 壳体屈曲分析中关于能力减弱系数的剖析[J]. 压力容器, 2012, 29(7):38-43. Huang Qing, Zhao Feiyun, Yao Weida. Dissection of ability reduced factors in shell buckling analysis [J].PressureVesselTechnology,2012, 29(7):38-43.(in Chinese)

[10] 石德新，王晓天. 潜艇强度[M]. 哈尔滨：哈尔滨工程大学出版社，1997：21-33.

[11] 冯亮, 佟福山. 基于强度稳定综合理论的深海潜器耐压圆柱壳极限强度的解算[J]. 哈尔滨工程大学学报, 2012, 33(2):1-5. Feng Liang, Tong Fushan. Ultimate strength calculation of pressurized cylindrical shells in deep-sea vehicle by the combined strength and stability[J].JournalofHarbinEngineeringUniversity,2012, 33(2):1-5.(in Chinese)

[12] 黎庆芬. 可潜器圆柱形耐压结构设计计算方法研究[D].华中科技大学，2007.

[13] 龚友根, 贺玲凤. 含有初始凹陷圆柱壳稳定承载能力的实验研究与数值计算[J]. 实验力学, 2010, 25(1):73-80. Gong Youggen, He Lingfeng. Experimental study and numerical calculation of stability and load carrying capacity of cylindrical shell with Initial Dent[J].JournalofExperimentalMechanics,2010, 25(1):73-80.(in Chinese)

[14] 王硕, 杨彦军, 岳祖润. 锁口钢管桩抗弯刚度折减行为及其影响因素分析[J]. 中南大学学报:自然科学版,2013, 44(4):1551-1555. Wang Shuo, Yang Yanjun, Yue Zurun. Analysis of reduced modulus action and influence factors in steel pipe sheet piles[J].JournalofCentralSouthUniversity:ScienceandTechnology,2013, 44(4):1551-1555.(in Chinese)

(责任编辑：贡洪殿)

Effectofribstiffnessonbucklingloadofstiffenedcylindricalshells

Bai Xu1, Li Jinhua2, Wang Xiaotian3

(1.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang Jiangsu 212003, China)(2.Institute of Oceanographic Instrument, Shandong Academy of Sciences，Qingdao Shandong 266001, China)(3.College of Shipbuilding Engineering, Harbin Engineering University, Harbin Heilongjiang 150001, China)

Through the relationship between energy and structural stiffness, the effects of bending stiffness, torsion stiffness and compression stiffness of ribs on the buckling loads of stiffened cylindrical shells are analyzed based on the critical buckling loads derived in this paper. Then the rib stiffness and shell stiffness are reduced to study the effects of different ribs on general stability of stiffened cylindrical shells and the reduced coefficient of a single rib is transformed to average reduced coefficient of all ribs. The effects of shell stiffness on the general stability of cylindrical shells are analyzed and the calculation method of general stability of cylindrical shells is given with the ribs stiffness and shell stiffness both reduced. This paper can provide a theoretical reference for research of the stability load-carrying capacity of stiffened cylindrical shell with initial imperfection and the design of stiffened cylindrical shells.

hydrostatic pressure; stiffened cylindrical shells; buckling load; stiffness of ribs; reduced stiffness method

10.3969/j.issn.1673-4807.2014.04.001

2014-02-21

国家自然科学基金资助项目(51409128,51409129)，江苏省高校自然科学研究项目资助(14KJB570001)

白 旭(1984—)，男，讲师，博士，研究方向为海洋水下工程结构力学、船舶与海洋结构物可靠性与风险分析.E-mail:baixu_just@126.com

U663.1

A

1673-4807(2014)04-0307-06