髋臼双柱骨折内固定生物力学稳定性的有限元分析
2014-08-30黄进成刘曦明蔡贤华王志华雷建银张继平
黄进成,刘曦明,蔡贤华,王志华,雷建银,张继平
近年来,我院利用前路特殊塑形钢板加方形区螺钉联合后柱螺钉治疗髋臼双柱骨折,在有效复位与内固定的同时,减少了手术创伤,缩短了手术时间及术中、术后并发症的发生率。随着研究及应用的进一步深入,临床上迫切需要对该内固定的生物力学稳定性进行研究。本文采用三维有限元方法对其进行分析,探讨其生物力学特性,为临床治疗提供必要的生物力学依据。
材料与方法
1 材料
健康志愿者1位,男性,40岁,身高175cm。16层螺旋CT机(德国 Siemens公司),Mimics10.1(比利时 Materialise公司),Ansys12.0-ICEM(美国ANSYS公司),Hypermesh V10.0(美国Altair公司),Abaqus 6.10(美国达索公司)。
2 方法
2.1CT数据的获取 对志愿者骨盆(从L5至股骨上1/3)进行CT断层扫描,层厚0.5mm,扫描过程中要求志愿者在骨盆纵轴方向上保证不动,扫描后将图像以DICOM格式保存在CT机中,刻录光盘,从而得到骨盆横截面的CT图像共473张。
2.2正常骨盆模型的建立 以DICOME格式将文件导入医学建模专用软件Mimics10.1中。进行骨盆的数字化三维重建。导入到Ansys12.0-ICEM中,进行网格划分。并根据各韧带起止点解剖位置在模型表面选取相应的节点建立韧带群。皮质骨被定义成厚度为1.5mm[1]。骨盆三维有限元模型参数见相关文献[2-5]。整个骨盆模型节点数为115940,单元数为112002(图1)。

图1 骨盆三维有限元模型
3 模型有效性的验证
将模型导入Abaqus 6.10软件。模拟双脚站立位。于S1椎体上终板设置刚性面,给予均匀分布载荷,模拟重力方向,大小为600N。边界条件: 为接近生理状态,只对股骨近端截面进行约束,限制6个方向的自由度(图2)。从弓状线起点经弓状线、耻骨上支至耻骨联合处作路径1; 沿髋臼缘前、上和后缘作路径2; 沿右骶骨岬经右髂骨、右坐骨、右耻骨下支至耻骨联合处作路径3。分别作出3条路径的应力-路径曲线(图3)。
图2a显示应力经骶骨向双侧骶骨翼、骶髂关节、髂骨,斜向下经弓状线、坐骨大切迹,传导至耻骨支及耻骨联合受力较小,结合图3应力分布曲线可看出,应力沿骶骨向髋臼的连线进行传导,骨盆前环受力较小。图2b位移以骶骨为中心,形成向两侧逐渐减弱的波浪形分布。从3条路径可以看出,沿路径1应力在弓状线起点处较大,后应力逐渐减小,至耻骨支应力稍增大; 沿路径2应力在髋臼后上方较大; 沿路径3应力分布在骶骨岬、骶髂关节及髋臼穹顶内侧骨皮质应力较大,且沿髋臼后柱应力逐渐减少,但至坐骨结节应力稍有集中。这一结果与理论认识及相关研究结果基本符合[5-7]。证明本研究建立的模型是有效的。

a.应力云图(MPa) b.位移云图(mm)
图2 有限元模型计算结果

图3 路径1、2、3上各节点的应力分布
4 骨折内固定模型的建立
通过网格的删减建立髋臼双柱骨折模型(图4)。分离移位<1mm。再建立A、B、C 3种内固定模型(图5)。钛板均模拟AO重建钛板(普通型,辛迪思公司),螺钉均模拟AO 3.5mm皮质骨螺钉(普通型,辛迪思公司)。材料均模拟钛合金,弹性模量为110GPa,泊松比为0.3[3]。后柱拉力螺钉在髂前上棘与坐骨棘连线与骨盆内面交点后上方5~25mm、弓状线外侧10~ 25mm区域内进钉,方向与方形区平行指向坐骨棘,所用螺丝钉长度为50~100mm。尽量保证螺钉与后柱主要骨折线角度在60°~90°范围内。其余内固定方式参考相关文献[8-10]。螺钉与骨组织、螺钉帽与钢板之间的约束是根据本研究模拟的螺钉尺寸,取预紧力大小87kgf,根据螺钉帽和螺纹部分面积的不同,施加于螺钉上,方向与接触面积垂直[11]。
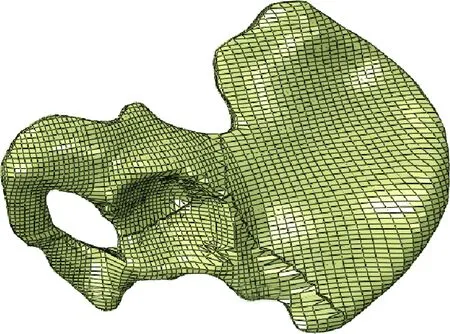
图4 髋臼双柱骨折有限元模型
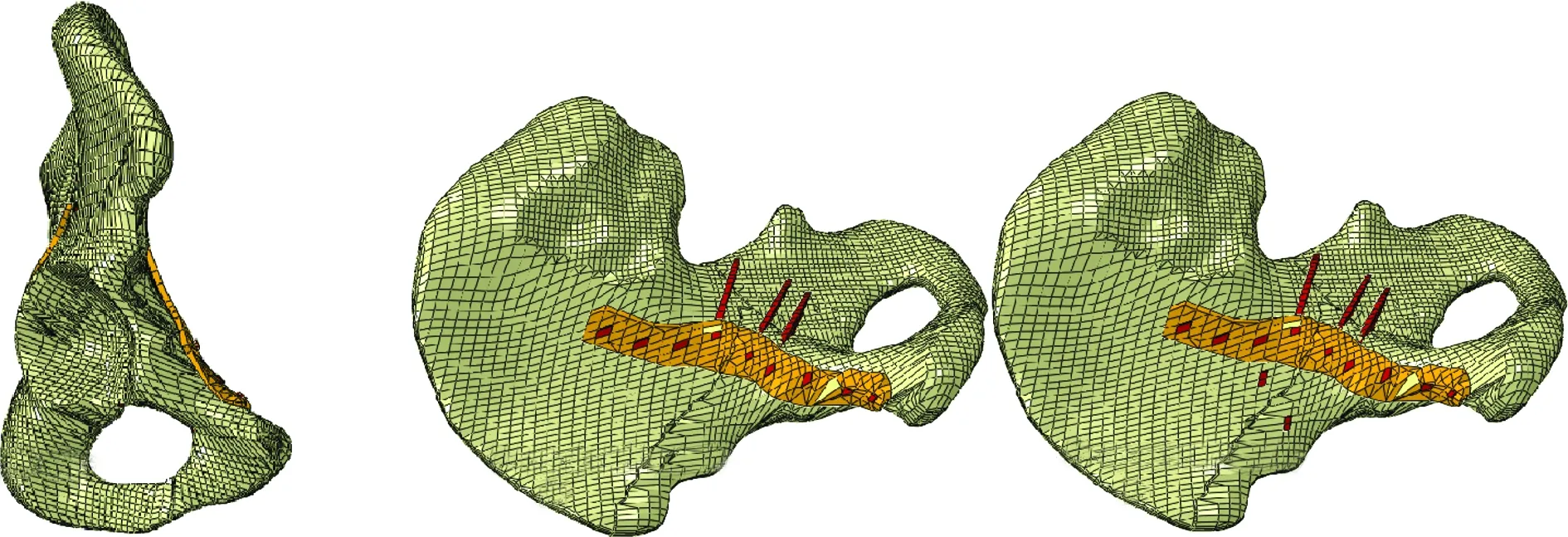
a b c
图5 3种内固定模型。a.双柱钛板; b.单纯前路特殊塑形钛板加方形区螺钉; c.前路特殊塑形钛板加方形区螺钉联合后柱螺钉
5 模型的约束加载与假设
将建好的有限元模型导入Abaqus 6.10软件。先后对坐骨结节及股骨下端进行约束,限制其6个方向的自由度。分别模拟坐位(Ⅰ)、站位(Ⅱ)骨盆受力。于S1椎体上终板设置刚性面,在几何中心给予载荷,方向模拟站立位时重力方向,大小为600N。假设条件为本实验所涉及的生物材料的材料力学特性均假定为均质连续和各向同性。
6 评价指标
6.1取髋臼内侧壁经过髋臼后缘至髋臼下缘骨折线上各节点组成一骨折线路径,测量骨折线路径上各节点的位移。比较骨折线路径上各节点的位移大小。位移越大则越不稳定。
6.2比较各种内固定模型上髋臼区最大位移及最大应力,位移及应力越大则越不稳定。
7 统计学处理
采用SPSS 19.0软件统计分析,先进行方差齐性判断,再进行单因素方差分析比较差异,如果差异有显著性意义时再用最小显著差异t检验两两多重比较,P<0.05表示有显著统计学意义。
结 果
从图6及表1可以看出,在各种骨折模型上,对于骨折线路径上各节点平均位移均表现为A>B>C,经单因素方差分析发现在坐位时,A与B、C的差异均具有明显统计学意义(P<0.05),但B与C及站位时三者的差异无明显统计学意义(P>0.05)。从表2可以发现,在坐位及站位下,各种内固定模型上,髋臼区的最大位移及最大应力均表现为A>B>C。
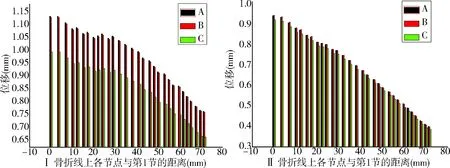
图6 分别在坐位(Ⅰ)、站位(Ⅱ)下,A、B、C 3种内固定后模型骨折线上节点的位移比较
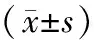
表1 坐位(Ⅰ)、站位(Ⅱ)下,骨折线上节点位移比较及方差分析
Pa: A与B比较的显著性; Pb: A与C比较的显著性; Pc: B与C比较的显著性

表2 坐位(Ⅰ)、站位(Ⅱ)下,3种内固定术后髋臼区最大位移及最大应力
讨 论
对于累计方形区的髋臼双柱骨折,双柱钛板为临床上最常采用的固定形式。但需要前后联合入路进行复位与固定,导致暴露损伤大、手术时间长、失血量大及术后感染等并发症发生率高等缺点。为了达到对骨折的有效复位与固定,减少手术创伤,有学者经单一前入路用重建钛板固定前柱,再在髋臼上缘平行于方形区通过重建钛板用3颗长螺钉进行内固定,但这种内固定需要避开髋臼最薄处,在髋关节周围进行,稍有不慎螺钉就会进入关节,导致内固定失败[12-13]。如何在对骨折进行有效内固定的前提下,减小手术创伤,并防止螺钉进入关节,再次成为了研究的焦点。我院从2005年开始采用前路特殊塑形钛板加方形区螺钉治疗髋臼双柱骨折取得了一定的效果。但实践操作中我们发现,后柱复位后,如不先进行简单的固定,不利于方形区螺钉的植入,甚至导致复位的丢失,反复复位使手术时间延长并增加手术创伤。为了弥补这一缺点,骨折复位满意后,首先用1~2枚后柱螺钉对其进行固定,更有利于方形区的复位及特殊塑形钛板加方形区螺钉的固定。从而进一步增强了内固定的效果,方便了复位固定,并扩大了单一前入路手术的适应证。
本实验在以前柱承力为主的站位及以后柱承力为主的坐位对3种内固定治疗髋臼双柱骨折术后模型进行了较全面的力学特性分析及对比。在坐位状态下,A、B、C 3种内固定模型在骨折线节点位移均数上表现为A>B>C,且A与B和C之间的差异具有明显统计学意义,在站位时骨折线节点位移均数亦表现为A>B>C,三者差异无明显统计学意义。坐、站位下髋臼处的最大应力及最大位移均表现为A>B>C,这说明前路特殊塑形钛板加方形区螺钉联合后柱螺钉内固定治疗髋臼双柱骨折较双柱钛板内固定具有明显好的生物力学稳定性。具有不亚于单纯前路特殊塑形钛板加方形区螺钉内固定的生物力学稳定性。加上该内固定具有较双柱钛板内固定更小的创伤,又有较单纯的前路特殊塑形钛板加方形区螺钉更方便的复位及更广的适应证,因此在临床上值得尝试。
目前在髋臼双柱骨折治疗中存在手术创伤大、出血多、操作难度大,术后并发症较多等主要问题。然而其治疗的关键又是精确的骨折复位和稳定的内固定,为了达到这一目的,亟需研究更安全、微创、稳定的手术方式。本文对骨盆模型进行了各向同性材料的赋值,在不失真的情况下对骨盆模型进行了一系列形态学处理,完成了骨盆和内固定物的重建。模拟了髋臼双柱骨折模型,并对该骨折模型进行了3种方式的内固定,并进行了有限元模拟与分析,比较其不同力学特性指标。根据比较结果得出3种方式稳定性差异,验证了前路特殊塑形钛板加方形区螺钉联合后柱螺钉内固定的生物力学稳定性,为髋臼双柱骨折的治疗提供了一种不仅更稳定、而且更微创、安全的内固定方式。但模型本身忽略了肌肉对骨盆生物力学的影响,在骨盆模型及内固定模型上也进行了一定的简化处理,分析结果和真实情况有一定的差异。在未来的研究工作中,将不断完善该骨盆模型,增加肌肉的建模,并且在更多的髋关节位置下进行分析,使分析实验条件更接近真实状况。
参考文献:
[1] Anderson AE,Peters CL,Tuttle BD,et al.Subject-specific finite element model of the pelvis: development, validation and sensitivity studies[J].J Biomech Eng,2005,127(3):364-373.
[2] McLauchlan GJ,Gardner DL.Sacral and iliac articular cartilage thickness and cellularity: relationship to subchondral bone end-plate thickness and cancellous bone density[J].Rheumatology(Oxford),2002,41(4):375-380.
[3] Zheng N, Watson LG, Yong-Hing K. Biomechanical modeling of the human sacroiliac joint[J].Med Biol Eng Comput,1997,35(2):77-82.
[4] Walker JM.The sacroiliac joint: a critical review[J].Phys Ther,1992,72(12):903-916.
[5] Phillips AT,Pankaj P,Howie CR,et al.Finite element modelling of the pelvis: inclusion of muscular and ligamentous boundary conditions[J].Med Eng Phys,2007,29(7):739-748.
[6] Dalstra M,Huiskes R,van Erning L.Development and validation of a three-dimensional finite element model of the pelvic bone[J].J Biomech Eng,1995,117(3):272-278.
[7] 李正东,邹冬华,刘宁国,等.人体骨盆有限元模型的建立及其在法医学鉴定中的应用价值[J].法医学杂志,2010,26(6):406-412.
[8] 蔡贤华,吴咏德,刘曦明,等.前路钛板加方形区螺钉治疗髋臼双柱骨折的站立位力学分析[J].中国矫形外科杂志,2013,21(6):595-601.
[9] 蔡贤华,刘曦明,王国栋,等.前路钛板结合方形区螺钉内固定治疗涉及方形区的髋臼骨折[J].中华创伤骨科杂志,2013,15(2):102-106.
[10] 倪卫东,高仕长,梁熙.前后联合入路手术治疗复杂髋臼骨折[J].中华创伤杂志,2008,24(2):126-128.
[11] 吴淑琴,潘宏侠,裴葆青.髋臼横断骨折后柱长/短钢板内固定的有限元建模及分析[J].北京生物医学工程,2011,30(1):1-4.
[12] Devon M,Eben A,Florian G,et al.Operative treatment of acetabular fractures in an older population through a limited ilioinguinal approach[J].J Orthop Trauma,2012,26(5):284-289.
[13] Lin HH,Hung SH,Su YP,et al.Cerclage wiring in displaced associated anterior column and posterior hemi-transverse acetabular fractures[J].Injury,2012,(43):917-920.
