旋转式平台惯导系统随机误差自补偿技术研究

杨建业，范小虎，赵旭阳，汪立新(.第二炮兵工程大学士官学院，山东青州6500;.第二炮兵工程大学自动控制工程系，西安7005)

旋转式平台惯导系统随机误差自补偿技术研究

杨建业1*，范小虎1，赵旭阳1，汪立新2
(1.第二炮兵工程大学士官学院，山东青州262500;2.第二炮兵工程大学自动控制工程系，西安710025)

针对旋转式平台惯导中旋转运动对惯性仪表的随机误差是否有抑制的问题，在建立旋转式平台惯导系统误差传播方程的基础上，利用积分换元法建立了台体旋转前后系统导航误差与噪声相关函数间的数学表达式，讨论了旋转运动对白噪声和3种典型有色噪声的抑制情况。得出了旋转运动对白噪声无抑制、在旋转速率满足一定条件时对典型有色噪声有抑制的结论。最后通过仿真验证了理论分析的正确性。研究结果为旋转式平台惯导系统的工程设计、改进提供一定的理论支持。

旋转;平台惯导系统;随机误差;自补偿

将旋转平均技术应用于平台惯导系统可以有效抑制惯性仪表常值误差，提高平台惯导系统的自主导航精度。在国外将采用了旋转平均技术的此类平台系统称为Carouseling Gimbaled Inertial Navigation System［1］，文中将此译为旋转式平台惯导系统。国外对旋转式平台惯导系统的研究已经非常成熟，且在美、俄等国的海军舰艇、飞机上已得到成功应用［2-6］。目前国内许多单位已经对旋转平均技术在惯导系统上的应用进行了深入的研究，相关单位已有原理样机面世。但国内文献对旋转式惯导系统的研究主要集中在常值误差的自补偿机理和初始对准方面［7-8］，而对随机误差的自补偿机理研究相对较少。本文将对旋转式平台惯导系统随机误差的传播特性进行研究，探讨平台台体的旋转运动对白噪声和典型有色噪声的抑制情况。

1 旋转式平台惯导误差传播方程

参照文献［9-10］分别定义坐标系:i为地心惯性坐标系、e为地球坐标系、g为地理坐标系、N为导航坐标系、T为理想平台坐标系、P为实际平台坐标系、c为计算坐标系。

与普通平台惯导系统不同，在旋转式平台惯导系统中引入了一个新坐标系——“虚拟平台坐标系P'”，将其定义为台体未加调制指令时的实际平台系，理想情况下该坐标系应当与T系重合。将P'系相对T系的误差角定义为旋转式平台惯导系统的姿态误差角。在普通平台惯导系统中，P'系与P系重合，姿态误差角的定义退化为P系相对T系的误差角，与平台惯导系统中姿态误差角的定义相一致。在文献［11-13］的基础上建立旋转式平台惯导系统的误差传播方程，如下所示。

速度误差传播方程:

姿态误差传播方程:

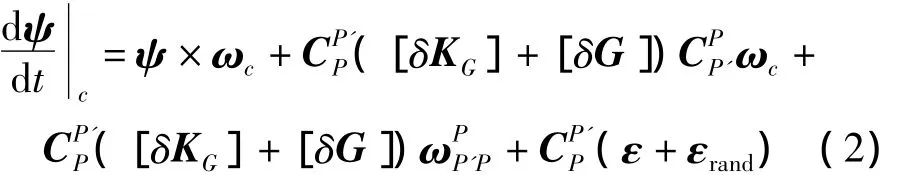
其中，▽与ε分别为加速度计和陀螺仪的常值误差，▽rand与εrand分别为加速度计和陀螺仪的随机误差。对常值项、安装误差、标度因数误差的抑制情况笔者已在相关文献中进行了讨论，本文将研究旋转对随机误差的抑制情况，将以旋转对加速度计随机误差的抑制为例来研究旋转式平台惯导系统随机误差的传播特性。由式(1)可得，旋转前加速度计随机误差引起的导航误差项为▽rand，旋转后变为CP'P▽rand。

设坐标OXNYNZN相对惯性空间不动，OXPYPZP相对OXNYNZN绕OZN轴旋转，载体在XOY确定的平面内运动，则台体不旋转时加速度计随机误差引起的速度误差为:

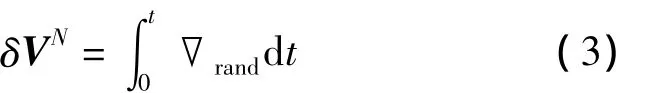
台体旋转时速度误差变为:

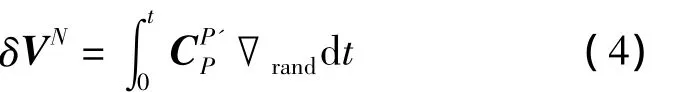
其中

为了分析方便，假设▽yrand=▽zrand=0，只讨论在随机误差▽xrand激励下，旋转前后δVN方差的变化情况。

2 导航误差方差与噪声相关函数间的关系

2.1 积分换元法

设f(x，y)在xOy平面上的闭区域D上连续，变换

将uOv平面上的闭区域D'变为xOy平面上的D，且满足:

①x(u，v)，y(u，v)在D'上具有一阶连续偏导数;

②在D'上雅可比式

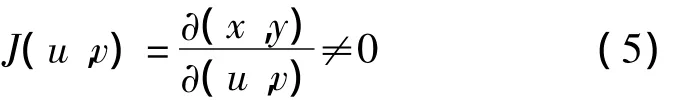
③变换T:D'→D是一对一的，则有:

2.2 导航误差方差与噪声相关函数间的关系

设▽rand=［▽xrand0 0］T，▽xrand为平稳随机过程，其自相关函数为:

则δVx(t)、δVy(t)及δVz(t)均为随机过程，当台体未旋转时，其自相关函数为:

对式(8)的积分变量进行下列变换:

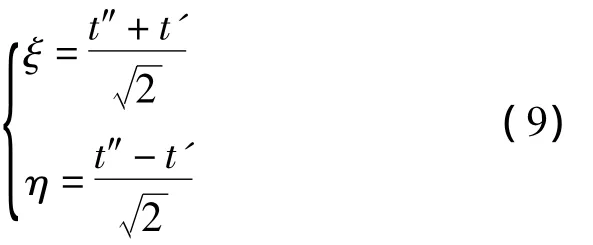
在t1=t2=t 的条件下，利用换元定理进行换元，变换前后积分区域如图1所示。

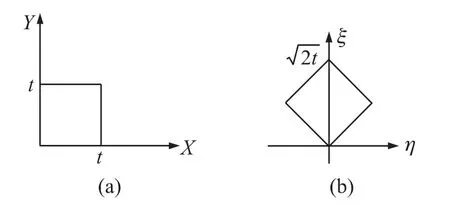
图1 变换前后的积分区域

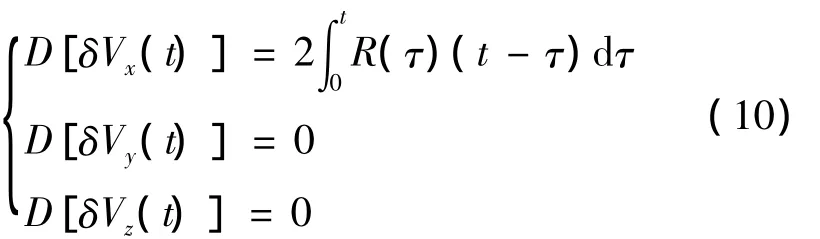
其合速度误差的方差为:

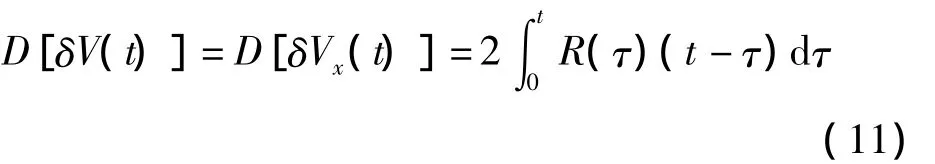
当台体旋转时，速度误差的自相关函数为:

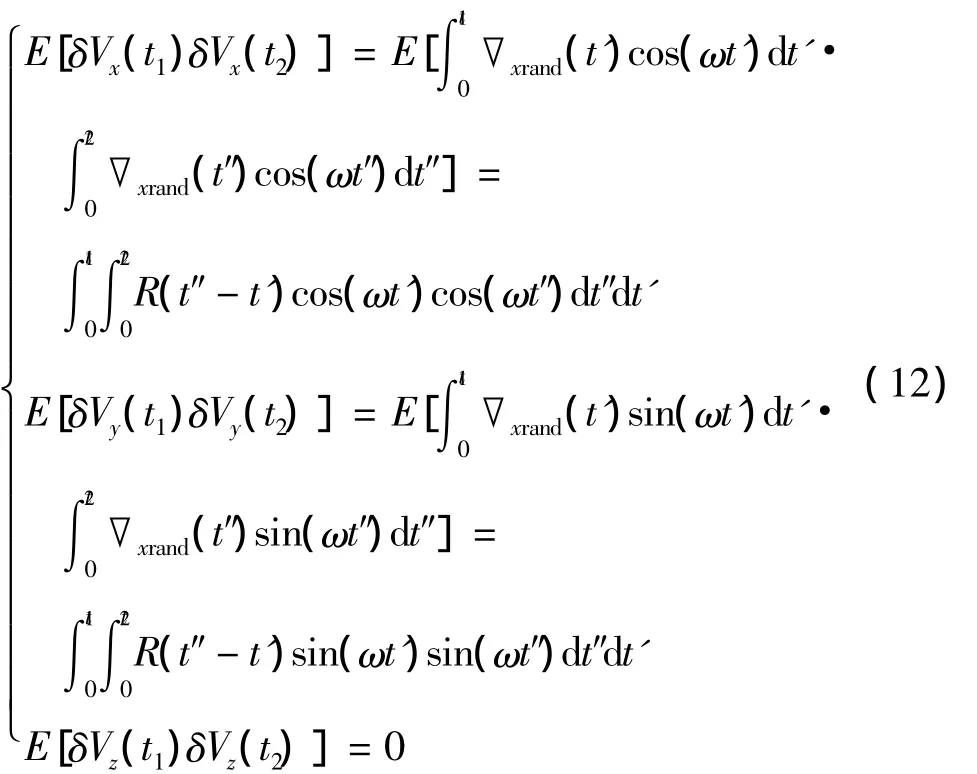
在t1=t2=t的条件下，将变量η变换为τ=，进行积分换元后得:

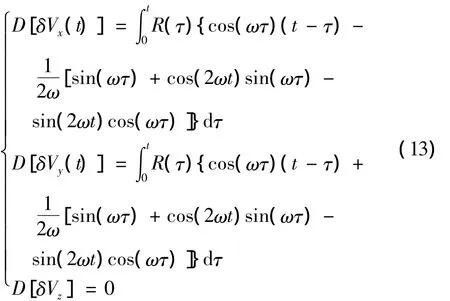
台体旋转时合速度误差为

则其自相关函数为:

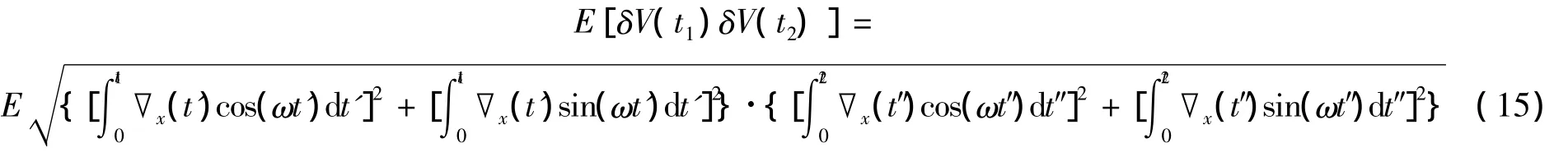
当t=t1=t2时，由式(13)和式(15)可得，台体旋转时合速度误差方差为:

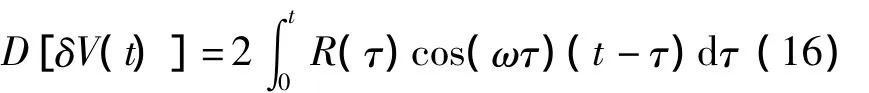
2.3 旋转运动对白噪声抑制分析

设白噪声的自相关函数R(τ)=Nδ(τ)，δ(·)为δ函数，当台体未旋转时

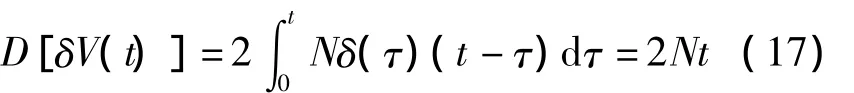
当台体旋转时

由式(17)和式(18)得，台体旋转前后速度误差的方差表达式相同，即旋转对白噪声没有抑制作用。

2.4 旋转运动对典型有色噪声抑制分析

本小节将研究旋转对3种典型有色噪声的抑制情况，3种有色噪声的自相关函数分别为:

当台体不旋转时，将噪声自相关函数的表达式代入式(11)得:

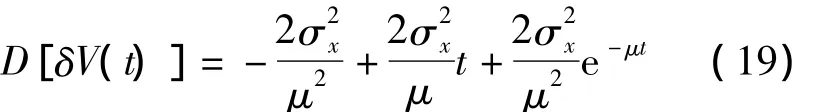
当台体旋转时，将噪声自相关函数的表达式代入式(16)得:

由式(19)和式(20)可以看出，速度误差的方差由常值项、随时间增长项和周期项三部分组成，其中对方差贡献较大的是随时间增长的项。

当台体不旋转时，速度误差的方差表达式为:

当台体旋转时，速度误差的方差表达式为:

当台体不旋转时，速度误差的方差表达式为:

台体旋转时，速度误差的方差表达式变为:

3 仿真及结果分析

3.1 仿真

(1)对有色噪声一的抑制

取σx=0.01，μ=0.01，图2示出旋转前后速度误差方差的对比关系(ω=3(°)/s)，图3为随时间增长项系数与旋转速度ω的函数关系。

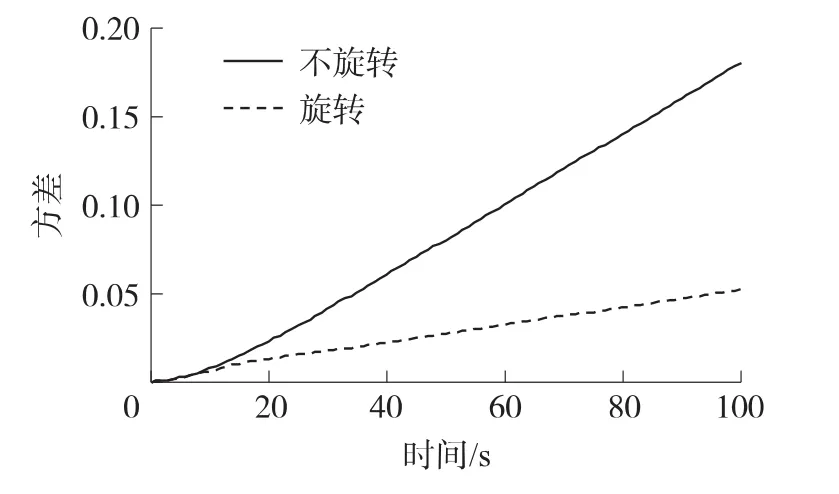
图2 速度误差方差与时间的关系(R(τ)=σ2x e-μ|τ|)

(2)对有色噪声二的抑制

图3 随时间增长项的系数与旋转速率间关系(R(τ)=σ2x e-μ|τ|)

取σx=0.01，λ=μ=0.01，图4示出旋转前后速度误差方差的对比关系(ω=3(°)/s)，图5为随时间增长项的系数与旋转速度ω的函数关系。

图4 速度误差方差与时间的关系(R(τ)=σ2x e-μ|τ|cosλτ)

图5 随时间增长项的系数与调制速率间关系(R(τ)=σ2x e-μ|τ|cosλτ)

(3)对有色噪声三的抑制

取σx=0.01，λ=μ=0.01，图6示出旋转前后速度误差方差的对比关系(ω=3(°)/s)，图7为随时间增长项的系数与旋转速度的函数关系。

图6 速度误差方差与时间的关系

图7 随时间增长项的系数与调制速率间关系

3.2 结果分析

由图2、图4及图6可得出，在台体以ω= 3(°)/s旋转时，速度误差的方差变小，即在此种情况下旋转对文中的3种典型有色噪声均有抑制作用;由图3、图5及图7可得出，当旋转角速度ω满足一定条件时，随着ω的增大，随时间增长项的系数会极大减小，即提高旋转角速度可以增加对文中典型有色噪声的抑制效果。

综上所述，旋转对白噪声没有抑制作用，当调制速度ω满足一定条件时对文中的典型有色噪声有抑制作用。

4 结论

本文对旋转式平台惯导系统的随机误差传播特性进行了研究。推导了旋转前后各种噪声引起的导航误差方差与噪声自相关函数的关系式，讨论了旋转对白噪声及3种典型有色噪声的抑制情况。最后得出结论:对白噪声没有抑制，在一定条件下对文中所讨论的3种典型有色噪声有抑制作用。本文的研究成果为旋转式平台惯导系统的工程设计、改进提供了一定的理论支持。

［1］Mohinder S G，Lawrence R W，Angus P A.Global Positioning Systems，Inertial Navigation，and Integration［M］.2nd Ed.Wiley-Interscience:A John Wiley and Sons，Inc.，Publication，2007:26-27.

［2］Sciegienny J，Nurse R，Wexler J，et al.Inertial Navigation System Standardized Software Development Final Technical Report VolumeⅡofⅣINS Survey and Analytical Development［R］.The Charles Stark Draper Laboratory，Inc.，Massachusetts，USA.1976.

［3］王荣颖，许江宁，卞鸿巍，等.方位旋转式平台惯导系统的误差分析与仿真［J］.系统仿真学报，2009，21(15):4786-4789.

［4］Hays K M，Schmidt R G，Campbell J D，etal.A Submarine Navigator for the 21st Century［J］.IEEE，2002(4):179-188.

［5］Levinson D E，Horst J T，Willcocks M.The Next Generation Marine Inertial Navigator Is Here Now［J］.IEEE，1994(2):121-127.

［6］Lahham J I，Brazell J R.Acoustic Noise Reduction in the MK49 Ship’s Inertial Navigation System［J］.IEEE，1992(3):32-39.

［7］于旭东，龙兴武，王宇，等.激光陀螺单轴旋转惯导系统多位置对准技术研究［J］.传感技术学报，2011，24(6):824-828.

［8］于旭东，王宇，张鹏飞，等.单轴旋转惯导系统在晃动基座上的建模及误差分析［J］.传感技术学报，2009，22(2):289-292.

［9］秦永元.惯性导航［M］.北京:科学出版社，2007.

［10］谢列托维其C M.陀螺系统仪表误差的自动补偿［M］.赵荣先，雷传琪，谢和持，译.北京:国防工业出版社，1986.

［11］Savage P G.Strapdown Analytics［M］.Strapdown Associate，Inc.，Maple Plain，Minnesota.2000.

［12］Savage P G.Strapdown Inertial Navigation Integration Algorithm Design Part1:Attitude Glgorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(1):19-28.

［13］Savage P G.Strapdown Inertial Navigation Integration Algorithm Design Part 2:Velocity and Position Algorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(2):208-229.

杨建业(1983-)，男，青海乐都人，博士，讲师，主要从事惯性系统及其标定测试、新型惯导系统等方面的教学和科研工作，yangjianye2002@126.com;

汪立新(1966-)，男，湖北武穴人，教授、博士生导师。主要从事惯性系统及其标定测试、精确导航、新型惯导系统等方面的教学和科学研究。

Research on Auto-Compensation Technology of Random Error for Carouseling GINS

YANG Jianye1*，FAN Xiaohu1，ZHAO Xuyang1，WANG Lixin2

(1.The Second Artillery Engineering University，Qingzhou Shandong 262500，China; 2.The Second Artillery Engineering University，Xi’an 710025，China)

Based on the error propagating equations，the mathematical representation between navigation error and related functions of noise was obtained by using integral character.Random error propagating rule of Carouseling Gimbaled INS is explored，and the results thatthe platform’rotation could depress the typicalcolored noise while rotation angular velocity satisfied some condition and could not depress the white noise were obtained finally.Then it is proved thatthe theoreticalanalysis is feasible through simulation.The research provides certain theoreticalsupport for the engineering design and modification of GINS.

carouseling;GINS;radom error;auto-compensation

U666.12

A

1004－1699(2014)05－0637－06

2014-03-20

2014-04-17