活塞异形曲面造型技术研究

刘明晖 廖君慧 阳超华

(湖南江滨机器集团有限公司)

0 引言

活塞是内燃机中关键的运动件，同时承受热机载荷，工作环境十分恶劣。活塞外圆具有导向、支撑和散热等作用，是活塞的一个重要部位，无论是设计分析，还是制造检测，都代表着一个技术水平的指标。随着活塞设计技术的不断发展和完善，外圆已经由最初的圆柱演变成为中凸鼓形类椭圆状。在横向各个截面由高次类椭圆、椭圆和圆等组成;在纵向剖面由中凸鼓形段、直线段和锥段等组成;并且有时纵向各个截面的椭圆度是变化的，因而构成了一个复杂的自由曲面活塞外圆。

当今计算机技术高速发展，在现代工业中扮演了重要角色，CAD/CAE/CAM技术得到了广泛的应用。然而，由于活塞外圆的复杂性，目前没有一款三维建模软件能直接对其进行仿真建模。因此，在实际设计和分析中只是以圆柱替代实际外圆型面进行活塞建模，如图1所示。简化的模型给后续的CAE和CAM等工作的开展有时带来了一定影响，本文的研究工作就是如何利用现代计算机技术建立高精度的活塞外圆仿真模型。

1 活塞外圆型面造型

1.1 活塞外圆结构分析

图2是某活塞的外圆型线图，其在纵向由6段不同规律曲线组成，分别是裙部中凸鼓形段、Ⅱ环岸圆柱段、Ⅰ环岸锥形椭圆段、下侧镶圈圆柱段、上侧镶圈圆柱段和火力岸锥形椭圆段;横向所有椭圆段都为一次椭圆;一次椭圆度在纵向各段呈直线变化。

图1 活塞三维模型

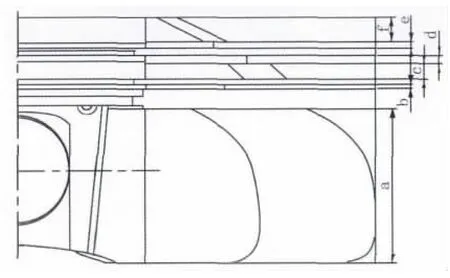
图2 活塞外圆型线图

如表1所示，是活塞外圆各高度处的设计数据，其包括活塞运行方向的直径减量和各段的椭圆度值。

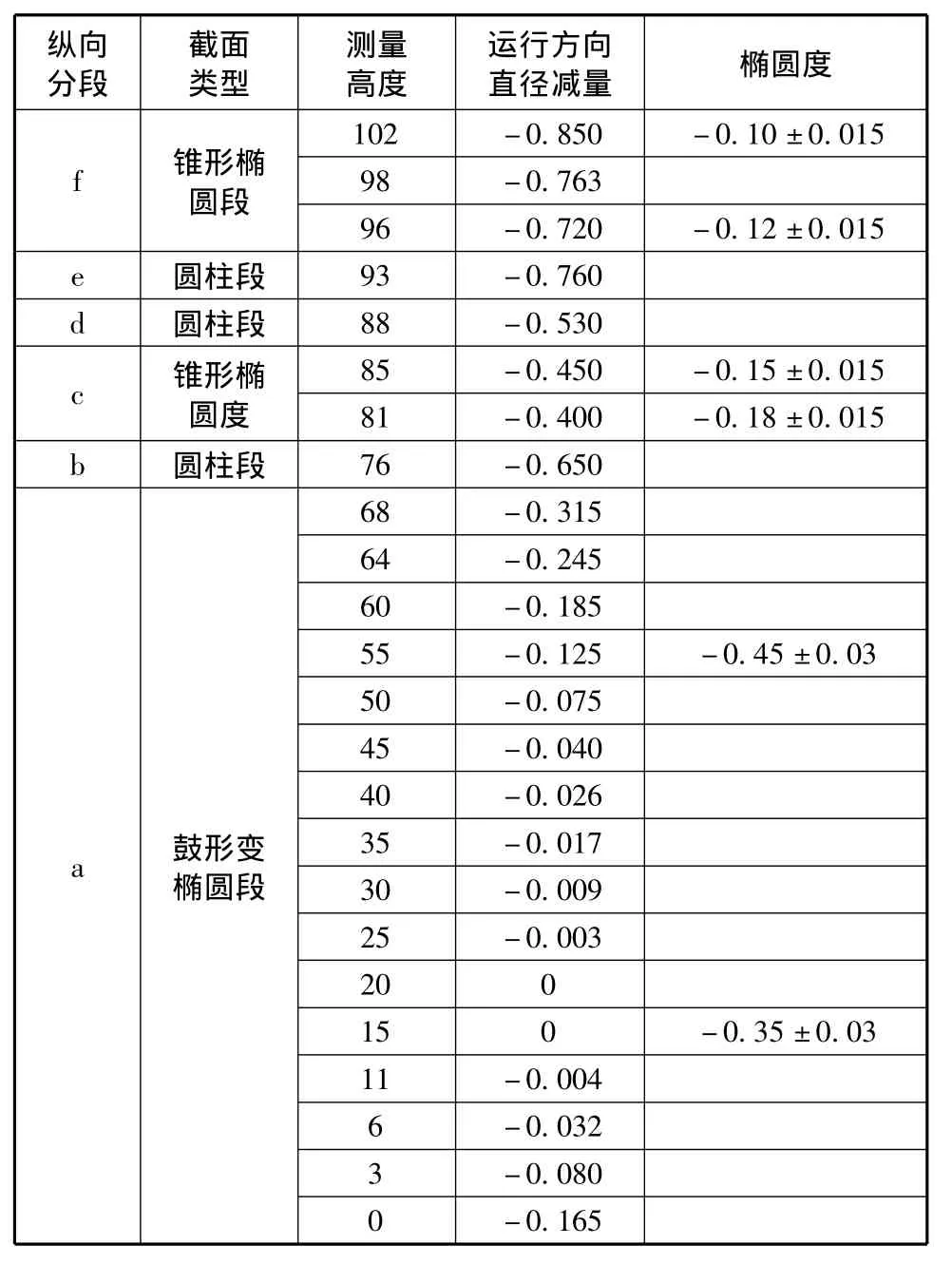
表1 活塞外圆数据

活塞外圆横截面设计时，由于其工作时既发生受力变形，也发生热变形，以及缸套的匹配性变形和合理的间隙量，通常设计成非圆截面，二次椭圆截面目前应用最广，其径向直径减量如式 (1)所示:

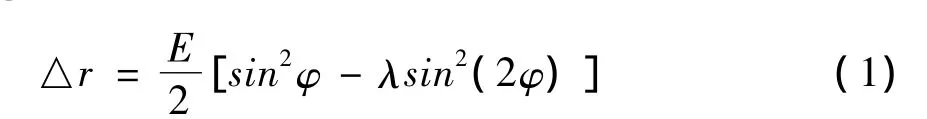
式中，E为椭圆截面的椭圆度;φ为椭圆截面角度值;λ为二次椭圆度丰满系数;△r为椭圆截面角度φ处的半径缩减量。本活塞横截面都为一次椭圆，既二次椭圆度丰满系数为0时的情况。

1.2 型面精密造型思路

造型技术主要用于三维动画造型、工程曲面造型和其它。三维动画造型着重于模型光顺性，希望得到一个良好的视觉效果，软件如Lightwave、Maya、PRMan、Animation、Truespace等，因此其不适合活塞外圆型面的造型。工程曲面造型要求模型具有较高的几何精度以及连续性等内在质量，常通过插值和逼近等手段来实现目标曲面。常用软件如:Pro/E、AutoCAD、CATIA、UG、Solidwoks等都能实现线面体模型功能，满足绝大多数的工程曲面造型需要〔1〕。

由于活塞外圆型面的复杂性，在上述的软件环境下直接进行建模，难度较大，不具备可操作性。因此，在已知型值点有限的前提下，需要借助于一种专业的数值计算软件根据外圆纵向和横向变化规律公式，把型值点计算出来，生成点矩阵文件。然后把点连成曲线，再导入造型软件环境下，建立外圆仿真曲面，最后完成精密造型工作〔2〕。具体造型思路如图3所示:

图3 造型思路图

1.3 确定造型参数

活塞外圆型面造型时，已知型值点越多，模型精度越高，然而产品图所提供的型值点数量有限，因此应根据活塞外圆设计原理对型值点进行插值计算求解，在纵向确定插值步长，在横向确定角度增量。

(1)纵向步长t

活塞纵向型线设计时，中凸鼓形段在宏观上一般每5mm设计一个型值点，微观上设计成瓦楞型或者波纹状结构，整个型面具有粗糙度要求，综合上述因素，按式 (2)对纵向步长t进行确定。

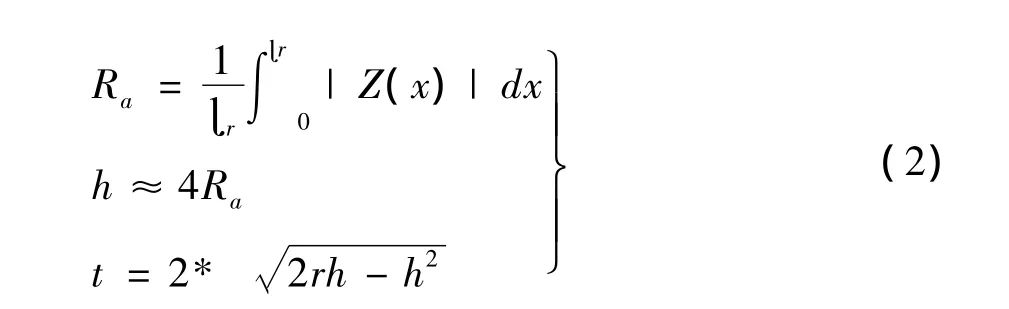
其中Z为型面波峰或波谷的长度;ɩr为粗糙度评定长度;活塞外圆型面粗糙度值Ra3.2 ～Ra4.8，取中差值0.004mm;h为型面波峰到波谷的距离;r为瓦楞或波纹圆弧半径值，r取值1.0mm，得到纵向步长t值为0.35mm。

(2)横向角度增量△α

活塞横截面为标准椭圆、高次类椭圆形或者偏心圆，下面以标准椭圆为例分析活塞型面精度与横向角度增量△α的关系，然后再确定△α值。

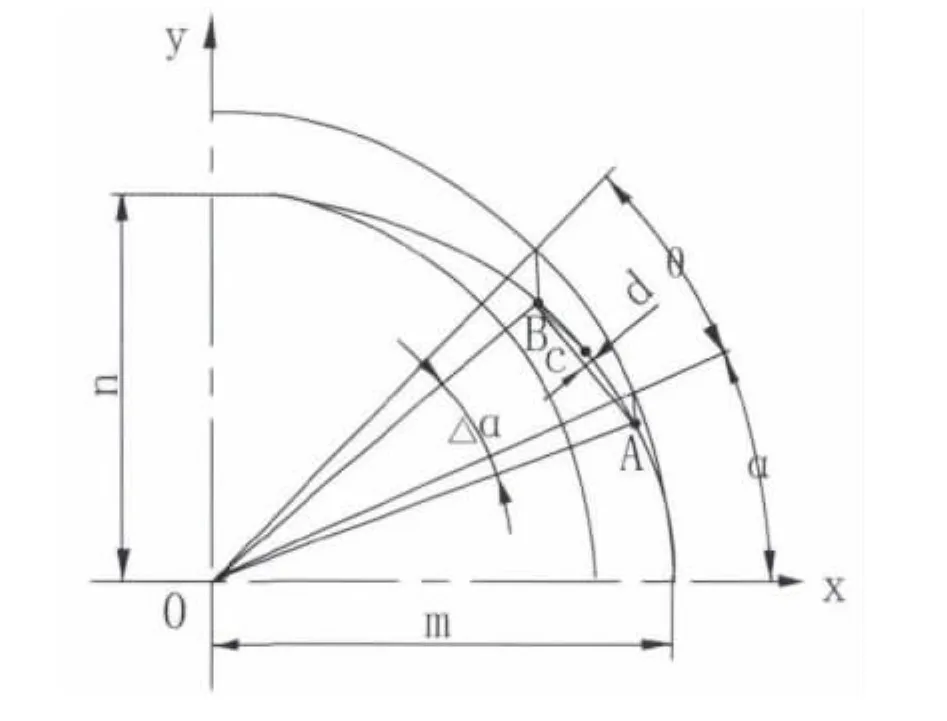
图4 横截面椭圆轮廓

如图4所示，A为椭圆上任意一点，α为其离心角，在增加△α后对应B点，其离心角为(α+θ)，m为椭圆的长半轴长度，n为椭圆的短半轴长度。根据标准椭圆公式式(3)可知，A点坐标值为(mcosα，nsinα);B 点坐标值为(mcos(α + θ)，nsin(α + θ))，这样可以确定直线AB的方程式。

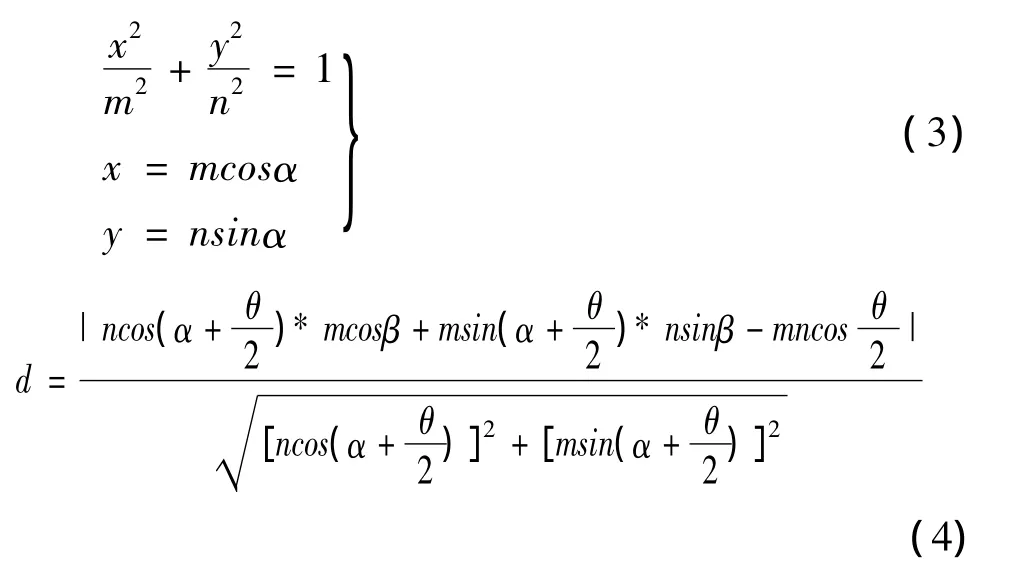
在AB所夹椭圆弧上任取一点C，令其离心角为β，求出点C到直线AB的距离d，d值大小如式(4)所示〔3〕，综合活塞长半轴与短半轴长度差值，得出:

其中 δ0为活塞外圆型面轮廓精度，取值0.01mm;k值等于活塞长半轴长度m，该活塞缸径110mm，取值55mm;根据式(5)可计算出横向角度增量△α值为不大于2.2°，考虑到模型计算问题，△α取值2.0°。

1.4 Matlab环境下型值点求解

在工程界著名的数学软件主要有四个，分别是Maple、MathCAD、MATLAB和 Mathematica。MATLAB以矩阵为基本数据单位，是数值计算的先锋，在其环境下求解型值点，具有下列优点:

(1)矩阵计算能力强;

(2)图形处理功能强;

(3)输入方面方便。

因此，根据上述的初始型值点、半径减量变化规律以及相关参数在MATLAB 7.11.0中编制M文件〔4〕〔5〕，其部分代码如下:

图5 活塞外圆型线验证图

运行M文件，生成图5所示的活塞外圆型线验证图，与图2进行对照，如果两者相符，输出点矩阵文件“Hs110.txt”，否则进行修改并调试。

1.5 Pro/e环境下活塞外圆型面造型

MATLAB输出文件“Hs110.txt”是型值点的x、y、z坐标值，其三维仿真图如图6所示，共计63541个点构成活塞外圆型面。面对如此庞大的数据，在Pro/E环境中以经过点创建曲线，然后再构成曲面是不现实的〔6〕。因此，首先应对型值点进行编辑，以文件的形式创建曲线，然后再根据曲线建立型面，编辑和创建方式如下:

图6 型值点三维仿真图

(1)以记事本打开文件“Hs110.txt”;

(2)增加如下命令，建立180条曲线;

(3)文件另存为“Hs110.ibl”;

(4)把“Hs110.ibl”导入Pro/E建立曲线;

(5)根据曲线建立混合曲面;

图7 活塞外圆型面

其中，步骤 (2)建立180条曲线的时候，应该注意点矩阵纵向排列的起始点;步骤 (4)所生成的曲线如图7左图所示;步骤 (5)所建立的曲面如图7右图所示。

1.6 模型精度分析

对于完成的活塞外圆型面，首先进行斑马分析和高斯分析，以确定造型时失真最大的地方，然后对该处进行精度分析，从而得出整个模型的精度。

斑马分析也称反射分析，其利用一组平行光投影到分析曲面，阴影顺化质量代表曲目质量。高斯分析也叫着色曲率分析，根据色标显示的其颜色范围内的高斯值来判断曲面的质量。图8中左图所示为斑马分析结果，其表明在活塞型面头部沟槽处阴影边界呈锯齿状，右图为高斯分析结果，同样表明该处曲面片之间存在跳色，其余部位质量良好。

图8 型面分析图

根据分析结果，取头部81mm处做精度分析。在该高度处的型面上通过活塞中心线建立两两对应的测量点，各点在截面圆周上相隔10°，如图9所示，测量各对应点的距离如表2所列。

图9 81mm高度处

表2 81mm高度处数据分析 (单位:mm)

表中偏差值结果显示，在0°和10°处理论值和测量值相差0.001，其余全部吻合，证明所建模型精度完全达到要求。

2 结束语

为了建立活塞外圆型面的精确模型，以适应设计分析及制造的需要，本文以某一活塞为实例逐步介绍了生成高仿真活塞外圆模型的整个原理和过程。首先确立造型的方法和参数，然后在Matlab环境下求解活塞外圆型值点，其三对型值点矩阵数据进行转换和编辑，再导入Pro/e环境下生成自由曲线并建立模型，最后对建立好的模型进行了分析，分析结果表明其精度完全符合要求。

〔1〕朱心雄.自由曲面造型技术〔M〕.北京:清华大学出版社，2000.

〔2〕高奇，李成英.活塞裙部中凸变椭圆型面虚拟设计〔J〕.辽宁工业大学学报，2011，31(6):361－363.

〔3〕刘加孝.宏程序铣削椭圆轮廓离心角增量值的计算方法〔J〕.机械制造与研究，2009，38(6):33－34.

〔4〕史立新，陈云富，王超群.基于Matlab的中凸椭圆活塞裙部曲线拟合〔J〕.组合机床与自动化加工技术，2007(7):24－25，29.

〔5〕刘明晖.柴油机活塞外圆型面设计及参数建模研究〔D〕.长沙:湖南大学，2013，34－40.

〔6〕申胜男，张继春.基于Pro/e的内燃机活塞裙部精确造型〔J〕.机械工程师，2006(4):35.