基于蚁群算法的多目标优化技术研究
2014-08-28陈凤莲汤健超
肖 菁, 陈凤莲, 汤健超
(1.华南师范大学计算机学院,广州 510631;2.武汉大学软件工程国家重点实验室,武汉 430072)
现实生活中的许多优化问题通常存在带有多个约束条件的多个目标需要被同时优化,多目标优化是要找到一个能同时满足所有优化目标的解. 一般情况下,这些目标之间是相互冲突的,改善了一个子目标的性能,可能会影响其他子目标的性能. 因此,解决多目标优化问题,需要找的是一组折衷解集使各目标尽可能达到最优. 多目标优化问题与单目标优化问题的本质区别在于多目标优化的解是由多个Pareto最优解组成的集合.
在科学研究和工程应用等现实生活中,多目标优化问题(Multi-objective Optimization Problem,MOP)是热门的研究课题. 进化算法(Evolutionary Algorithms,EA)、粒子群优化(Particle Swarm Optimization,PSO)、蚁群算法(Ant Colony Optimization,ACO)等基于种群的智能算法具有较高的并行性,在求解多目标问题时一次运行能求得多个Pareto最优解. 因此,吸引了越来越多不同领域的学者利用这一类基于种群的算法求解多目标优化问题.
蚂蚁算法(Ant algorithm)最早由Dorigo等[1]提出,并逐渐发展为ACO算法. ACO是一种源于生物世界的仿生优化算法,同时也是具有高度创新的元启发式算法. 基本蚁群优化算法的搜索机制是基于转移概率,其信息素的更新是基于解的质量. 就单目标优化问题而言,这2种方式有利于蚂蚁的搜索朝着信息素浓度高的区域进行,并且更快地获得更好的解. 以旅行商问题(Traveling Salesman Problem, TSP)为例,将此问题用图1表示,每个点代表一座城市,蚂蚁会在经过的路径上释放信息素,越多蚂蚁经过的路径上信息素就越多,根据信息素的分布,蚂蚁较容易找到最短路径.
自Dorigo和Gambardella[2]首次将蚁群算法成功应用于旅行商问题后,许多学者利用蚁群算法求解多目标优化问题,这类算法就是多目标蚁群算法[3](Multi-objective Ant Colony Optimization,MOACO),被应用于科学研究、工程应用、通信网络以及生产管理等诸多优化领域并取得了良好的效果.

图1 蚁群算法求解旅行商问题示意图
调度(scheduling)问题是一类经典运筹问题,包括3个重要的要素:任务、资源和目标,是典型的NP-hard问题. 它广泛应用在离散制造工业和流程工业,目前已成为计算机集成制造系统(Computer Integrated Manufacturing Systems,CIMS)领域内的重要研究课题. 流水车间调度问题(Flow Shop Scheduling Problem,FSP)在同时需要考虑最大完工时间、总流程时间和机器闲置总的时间时成了一个典型的多目标优化问题. Yagmahan和Yenisey[4-5]结合蚁群优化和局部搜索的策略成功地将其问题进行了优化.
多目标最短路径问题(Multi-Objective Shortest Problem,MOSP)是传统的单目标最短路径的延伸,同时考虑多个相互存在冲突的目标且计算出一条有效的最短路径. 该问题在远程通信、运输和工程管理中都是最重要的问题之一. Ghoseiri和Nadjari[6]利用多目标蚁群优化算法解决双目标最短路径问题取得了很好的效果. Sun等[7]使用自适应算子对MOACO进行了改进,提出了算法分为2个阶段,在前期,使用一个更高的概率对解空间进行搜索,搜集有用的全局信息;在后期,使用自适应算子使得搜索空间减小,从而加速收敛.
针对多目标蚁群算法为目前研究热点,本文简要介绍了多目标优化问题、蚁群算法和Pareto最优解的定义,详细讨论了目前针对求解多目标问题所使用的蚁群优化算法,重点讨论了蚁群算法的内在并行性在多目标上的实现,分析了诸多学者研究多目标蚁群优化算法的具体情况. 最后对多目标蚁群优化算法的进一步发展提出了新思路.
1 多目标蚁群优化算法的一般模型
多目标优化问题可描述为:

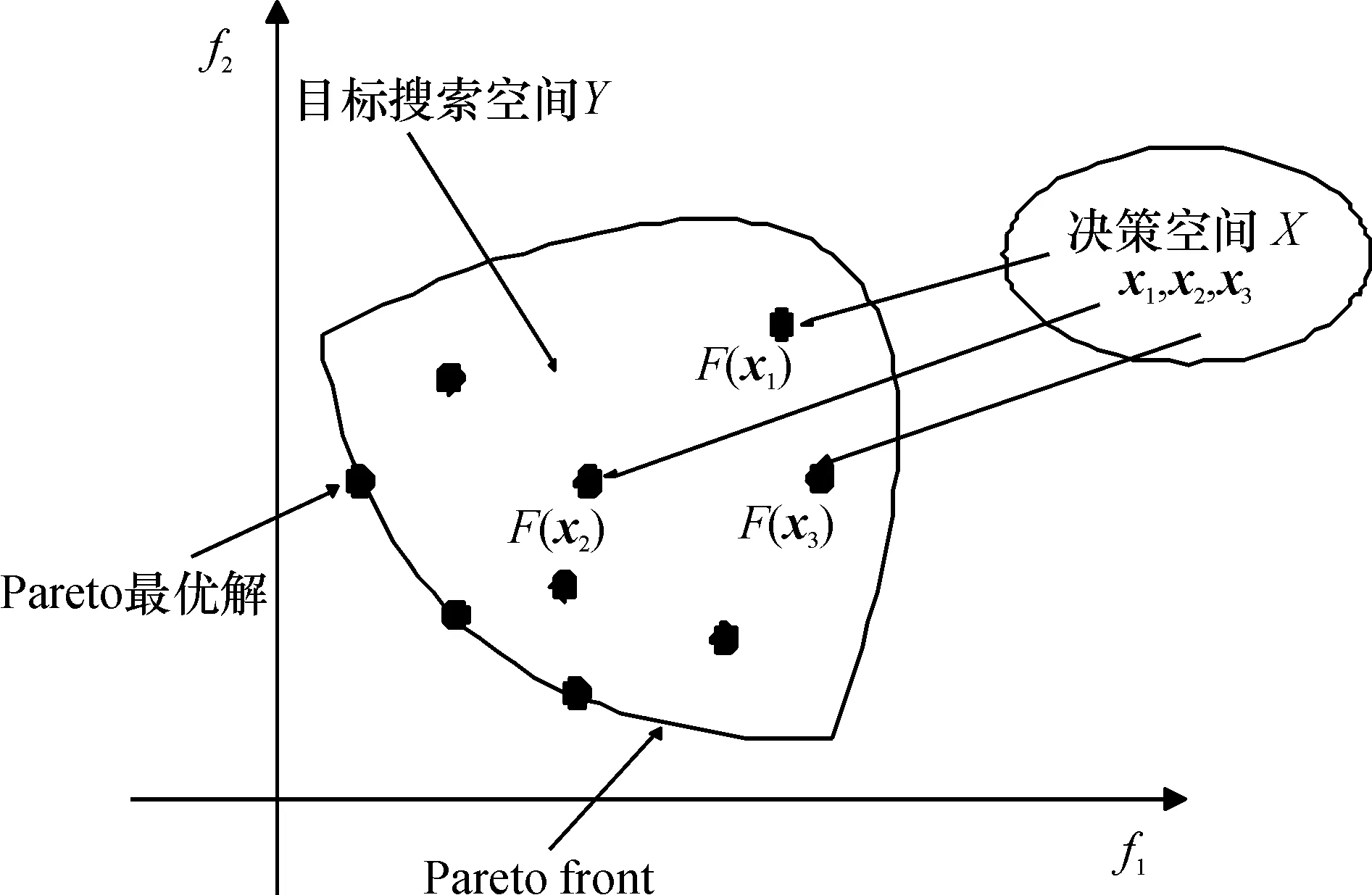
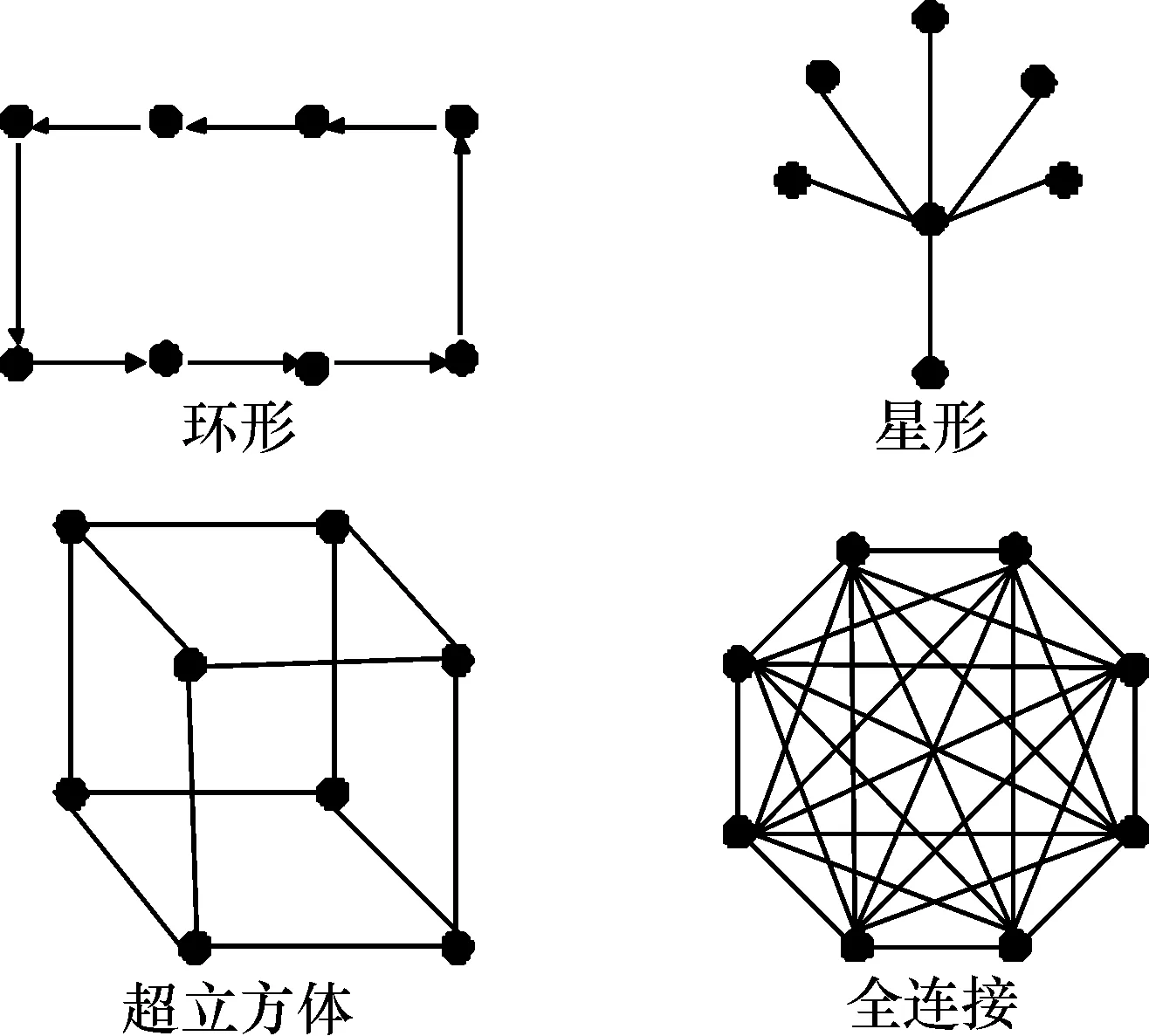
定义1 一个决策向量x1支配另一个决策向量x2(x1x2),当且仅当∀i=1,2,…,m,fi(x1)≤fi(x2)∧∃j=1,2,…,N,fj(x1) 定义3 所有Pareto最优解的集合称为Pareto最优解集P*. 表示如下: 其结构见图2. 图2 Pareto解集和Pareto前沿面 近年来,为解决多目标优化问题,学者们提出了多种蚁群算法. 本文选取了其中典型的3种多目标蚁群优化算法进行讨论. 将多目标优化问题分解成单目标优化问题时,通常使用加权法、契比雪夫法(Tchebycheff approach)和边界交集法等传统数学规划方法. 2007年,Zhang和Li[8]将这种传统的策略与进化算法相结合提出了一种新颖的基于分解的多目标进化算法(MOEA/D). 随后,很多学者在该算法的基础上提出了新的观点以解决不同的问题. 2013年,Ke等[9]在MOEA/D的基础上做了进一步的研究工作,将蚁群算法与多目标进化算法结合,提出了一个多目标进化算法——MOEA/D-ACO. 该算法与MOEA/D算法原理一样,首先将多目标优化问题分解为一定数量的单目标优化问题,然后用蚁群算法优化. 同时,蚂蚁由原来的一个群体被分成多个子群,并在此基础上引入了邻居蚂蚁,每只蚂蚁都有其邻居,并且一只蚂蚁对应于一个子问题. 每一个子群维持一个信息素矩阵,并且都有其自己的启发式信息矩阵. 每只蚂蚁结合邻居更新并记录其所对应子问题的当前最优解,并结合自己所在子群的信息素值和启发式信息构建每个子问题的解. 2012年,Cheng等[10]提出了基于分解的多目标蚁群优化(MoACO/D)的框架求解双目标的旅行商问题(bTSPs). 在该算法中,第一次将bTSP使用契比雪夫法分解成一定数量的子问题,蚁群以重叠的方式被分为多个子群,每个子群独立地、并行地使用单目标ACO优化其对应的子问题. 在这个框架的基础上,他们还将MoACO/D分别与蚂蚁系统(Ant System, AS)、最大最小蚂蚁系统(MAX-MIN Ant System, MMAS)和蚁群系统(Ant Colony System, ACS)对10组bTSP进行了实验并与MACS[11]、BIANT[12-13]、UNBI[12-13]进行比较,结果表明,在处理大规模的双目标旅行商问题时,MoACO/D的性能优于上述3种著名的多目标蚁群优化算法. 同年,Gao等[14]针对使用标量多目标优化技术处理多目标优化问题,提出了一个与概率模型结合的、基于分解的多目标评估分布估计算法(MEDA/D). 该算法使用先验经验和自学习的信息引导蚂蚁搜索子问题,并通过邻居之间的合作优化其子问题. Guntsch和Middendorf[15]提出了基于种群方法的蚁群优化算法(PACO),该方法增加了一个存放每一次迭代最优解的K规模的种群,当第K+1次迭代时,产生的最优解将采用先进先出的顺序替换种群中的一个解,信息素矩阵中的信息素也做相应的更新. 此信息素模型的更新策略适合解决动态优化问题,而且其有限的状态空间在设计新的启发式方法具有较高的扩展性. Angus[16]用一种密集种群(crowding population)替换技术扩展基于种群的蚁群优化算法解决多目标问题. 该算法通过选择性替换技术维持解的多样性,使解收敛在Pareto前沿面上. 尽管PACO显示了能较好地处理多目标组合优化问题的性能,但是尚未应用在多目标函数优化问题中. 随后,Angus[17]测试了PACO算法解决多目标函数优化问题的适应性. Kurniawan等[18]对于DNA序列优化和DNA序列的计算问题也使用了PACO算法进行优化. 在求解多目标优化问题的Pareto解集时,需要注意2个关键性的问题:(1)种群的收敛性问题,即如何使种群在各轮搜索所得解尽快地向Pareto前沿方向逼近;(2)种群的多样性问题,即如何使非支配解在Pareto前沿面上均匀分布. 针对这2个问题,人们提出了不同的算法. 基于Pareto解集蚁群优化算法(P-ACO)最初由Doerner等[19]提出应用在多目标组合优化问题,与经典ACS算法不同的是,每个目标的当代全局信息素不仅更新了最优解,同时更新了次优解. 在蚂蚁的整个搜索过程中将找到的非支配解存入一个外部Pareto解集中. 2008年,Häckel等[20]利用动态规划方法改进多目标最短路径问题的解逼近Pareto前沿面. 2013年,Mora等[21]引进了一个种群之间通信通过侦查蚁的岛屿模型,并且使用了一种适合搜索空间的邻居拓扑结构. 在很多实际的应用中,很多学者也利用了基于Pareto解集蚁群优化算法,如多目标电网规划(multi-objective power network planning)[22]、多目标拆卸线平衡(Disassembly Line Balancing Problem,DLBP)[23]等. 所有的策略都尽可能地覆盖Pareto前沿面,因此各个子群或者岛屿在其他子群的辅助下在有限的区域内搜索解,以找到更多高质量的解集. 蚁群算法在执行过程中,单只蚂蚁在一次循环中与其他蚂蚁的通信是通过信息素矩阵,能够异步更新,并且每只蚂蚁之间是相互独立的. 因此,蚁群算法本身隐含着一定的并行性,其本质上是一个分布式的方法. 随着问题的复杂度逐渐提高,蚁群算法需要考虑计算时间和资源,串行方式已不能满足. 因此,很多学者提出了一些蚁群算法的并行算法. 2011年,Mora等[24]提出了一个并行的多目标蚁群优化算法. 该算法在将蚂蚁分配在各节点时采用粗粒度并行,提出了2个不同的分布方式:Space Specialized Colonies(SSC)和Objective Specialized Colonies(OSC). SSC由一组独立的蚁群组成,各自在不同的区域搜索解,最后合并他们搜索到的最优解组成最后一组Pareto解. OSC与SSC不同的是其各子群只优化其对应的目标,最后将其合并成一组Pareto解. 此方法不仅提高了运行时间,最重要的是能够找到一组更好的非支配解和一个更好的Pareto分布. 对于并行蚁群算法中多个子群之间的拓扑结构一般分为4种:环形拓扑结构(Ring topology)、星形拓扑机构(Star topology)、超立方拓扑结构(Hypercube topology)和全连接拓扑结构(Fully-connected).以8个子群为例,其拓扑结构见图3[25-26]. 2007年,Ellabib等[25]在子群之间的交互采用了星形结构、环形结构和超立方体结构,提出了一种新的基于加权的信息交互机制,在研究这些交互机制对搜索行为的影响时采用了基于团队共识方法. Twomey等[26]在2010年也进行了大量的实验,他们在定向环、超立方体和全拓扑3种不同的拓扑结构上考虑了4种不同的通信策略:单向环形(Unidirectional ring)策略:在p个子群中,Ci只向C(i+1)mod p传递最优解并只接收C(i-1)mod p的最优解;超立方体(Hypercube):在这个模型中每个子群只接收和传递与之有边相连的子群的最优解;替代最差解(Replace-worst):子群Ci分析其他p-1个子群中的最优解,并将其代替本子群的最差解;全连接(Fully-connected):该模型与替代最差解模型类似,差别在于找出p-1个子群中的最优解与本子群中的最优解比较,取两者中的最优解. 同时Twomey还考虑了子群数量、蚂蚁的移动时间和局部搜索对算法的影响. 2010年,Jovanovic等[27]通过解决最小点覆盖问题,分析了并行执行时各子群之间不同的拓扑结构或通信策略对解搜索的影响. 2008年,Xiong等[28]从蚁群算法并行化过程中粒度处理标准和信息素的交互策略角度出发,提出了一个新的并行蚁群优化算法.该算法主要考虑了2个方面:一是如何将单个串行蚁群划分成多个相互独立的子群分配在多线程处理机中;二是在子群中如何管理和控制信息素的更新. 实验表明,对于解决大规模的TSP问题,PACO中节点的计算时间明显减少,性能优于串行蚁群算法.Yu等[29]提出了一个采用粗粒度并行、加权和变异操作的改进蚁群优化算法解决多车场路径问题. 因此,在研究蚁群算法的并行化时,需要解决对蚁群算法的分解、分解之后各子群直接地交互,同时还得考虑并行化过程中粒度处理的标准. 图3 4种不同的子群拓扑结构 为了提高解决多目标优化问题的性能,很多学者对原有多目标蚁群算法针对解决不同问题进行了相应的改进. 对算法的改进一般都是针对2个问题:一是提高Pareto解的多样性,二是使Pareto最优解覆盖最优前沿面. 自Bilchev和Parmee[30]提出CACO解决单目标问题,采用将遗传算法与蚁群算法结合来提高算法的性能. 2008年,Lee等[31]在求解多目标优化问题时,也采用此方法,遗传算法具有快速全局搜索能力,而蚁群算法具有较好的收敛速度,提高了解搜索的多样性和解的收敛速度. 提出与其他算法的结合,实现2个算法的优缺点互补的还有Thanushkodi和Deeba[32],他们将粒子群优化与蚁群优化结合,对于多机处理任务调度问题同样表现出优良的性能. Liu和Chen[33]则提出了一个基于多蚁群的方法来提高Pareto解的多样性.Chica等[34]引进了一种新的机制避免陷入局部收敛,并且使用由Middendorf等[35]提出的在解的构建过程中使用不同的状态更新规则的多目标蚁群方法引导每一代搜索多样性更好的解. 目前多目标蚁群算法的研究大部分集中在优化2个目标上,Bezerra等[36]提出了一个新的蚁群算法称为GRACE用于解决多目标最短路径问题. 该算法利用了Raith和Ehrgott[37]提出的两阶段策略. 在第一阶段的搜索过程中,引入了称为Logos的搜索策略,Logos-2和Logos-3分别对应于双目标和三目标,这个阶段的搜索减小了第二阶段的搜索空间,从而加快了第二阶段的收敛速度. 第二阶段采用单蚁群,蚂蚁将继续在相同的Pareto前沿面处搜索,目的是为了使大量的蚂蚁在相同的区域探索,提升第一阶段的搜索. 2013年,Bezerra等[38]对GRACE又进行了扩展,引申出7个不同的变体,他们之间的区别体现在蚂蚁提供的信息素在数值向量上不同. 多目标蚁群优化算法在解决众多实际问题时表现出较好的性能,对于现存的诸多方法按不同的标准可将其分为多种不同类. 如蚂蚁在当前决策点如何选择下一个节点,通常是依据信息素结构和启发式函数的定义[13]. 在处理多目标优化问题时,对于信息素结构通常会考虑2种不同的策略:第1种策略考虑使用一个信息素结构,蚂蚁释放信息素的量要集成多个目标的期望;第2种策略考虑用多个信息素结构,通常将蚁群分成多个子群对应不同的目标,每个子群拥有自己的信息素结构[9-10,16-17,24].多目标问题启发式函数的定义也有2种:一是不同的目标聚合成单一的启发式函数[16];二是不同的目标有其各自对应的启发式函数[9-10,24]. 关于解的奖励[39](Solutions to reward),在更新信息素时,需要考虑更新哪些解边上的信息素. 第1种是奖励当前迭代中最好的那个解[16]. 第2种是奖励当前的每一个非支配解[20]. 因此,可能会奖励所有在Pareto最优解集中的解,或者只奖励当前循环中最新加入的非支配解. 如前所述的基于分解的多目标蚁群优化则是将蚁群分成多个子群分配在各个目标上,每个子群共同维持一个信息素矩阵,每只蚂蚁都有其各自的启发式信息矩阵;基于Pareto的蚁群优化(P-ACO)使用了多个信息素矩阵和单一的启发式信息矩阵;基于种群的多目标蚁群优化(PACO)则是使用了多个信息素矩阵和多个启发式信息矩阵. 虽然多目标蚁群优化算法已被用来解决了生活中许多的多目标优化问题,但仍然存在一些缺陷. 单目标的蚁群优化算法在收敛分析方面有众多的研究,但是对多目标的收敛分析却很少,特别对Pareto解域的收敛性分析. 另外,多目标蚁群算法的实验分析通常是对二维的多目标进行,对于复杂的高维多目标优化问题的研究却很少,然而实际生活中的多目标问题通常是高维的.因此这些都将是多目标蚁群优化算法有待提高的地方,需要进一步开展研究. 参考文献: [1] Dorigo M,Maniezzo V, Colorni A.Antsystem:Optimization by colony of cooperating agents[J].IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics, 1996, 26(1): 29-41. [2] Dorigo M, Gambardella L M.Ant colony system: A cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation, 1997, 1 (1): 53-66. [3] Angus D, Woodward C. Multiple objective ant colony optimization[J]. Swarm Intelligence, 2009, 3(1): 69-85. [4] Yagmahan B, Yenisey M M. Ant colony optimization for multi-objective flowshop scheduling problem[J].Computers & Industrial Engineering, 2008, 54(3): 411-420. [5] Yagmahan B, Yenisey M M. A multi-objective ant colony system algorithm for flow shop scheduling problem[J].Expert Systems with Applications, 2010, 37(2): 1361-1368. [6] Ghoseiri K, Nadjari B. An ant colony optimization algorithm for the bi-objective shortest path problem[J].Applied Soft Computing, 2010, 10(4): 1237-1246. [7] Sun X K, You X M, Liu S. Multi-objective ant colony optimization algorithm for shortest route problem[C]∥International conference on machine vision and human-machine interface (MVHI10).Kaifeng, China, 2010:769-798. [8] Zhang Q F, Li H.MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731. [9] Ke L J, Zhang Q F, Battiti R. MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and ant colony[J]. IEEE Transactions on Systems Man and Cybernetics Part A-Systems and Human, 2013(99): 1-15. [10] Cheng J, Zhang G X, Li Z D, et al. Multi-objective ant colony optimization based on decomposition for bi-objective traveling salesman problems[J].Soft Computing, 2012, 16 (4):597-614. [12] Iredi S, Merkle D, Middendorf M. Bi-criterion optimization with multi colony ant algorithms[M]∥Evolutionary multi-criterion optimization.New York:Springer,2001,1993:359-372. [13] García-Martínez C,Cordón O,Herrera F. A taxonomy and an empirical analysis of multiple objectiveant colony optimization algorithms for the bi-criteria TSP[J]. European Journal of Operational Research, 2007, 180(1): 116-148. [14] Gao F, Zhou A, Zhang G X. An estimation of distribution algorithm based on decomposition for the multiobjective TSP[C]∥International conference on natural computation (ICNC12).Chongqing, China, 2012: 817-821. [15] Guntsch M, Middendorf M.A population based approach for ACO[M]∥Applications of evolutionary computing.New York: Springer-Verlag,2002, 2279: 72-81. [16] Angus D. Crowding population-based ant colony optimisation for the multi-objective travelling salesman problem[C]∥IEEE symposium on computational intelligence in multicriteria decision making(MCDM07).Honolulu, HI, 2007: 333-340. [17] Angus D. Population-based ant colony optimisation for multi-objective function optimization[M]∥Progress in artificial life. New York:Springer-Verlag, 2007, 4828: 232-244. [18] Kurniawan T B, Ibrahim Z, Khalid N K, et al. A population-based ant colony optimization approach for DNA sequence optimization[C]∥Asia international conference on modeling & simulation (AMS 09). Bali, Indonesia, 2009:246-251. [19] Doerner K, Gutjahr W J, Hartl R F, et al. Pareto ant colony optimization: A metaheuristic approach to multiobjective portfolio selection[J].Annals of Operations Research, 2004, 131(1-4): 79-99. [20] Häckel S, Fischer M,Zechel D, et al.Amulti-objective ant colony approach for pareto-optimization using dynamic programming[C]∥Proceedings of the 10thannual conference on Genetic and evolutionary computation(GECCO08).Atlanta, GA, USA,2008: 33-40. [21] Mora A M, García-Snchez P, Merelo J J, et al.Pareto-based multi-colony multi-objective ant colony optimization algorithms: An island model proposal[J].Soft Computing, 2013, 17(7):1175-1207. [22] Yang F, Rong H, Cao J L, et al. Multi-objective power network planning based on improved pareto ant colony algorithm[C]∥Asia-pacific power and energy engineering conference(APPEEC09).Wuhan,China, 2009:1-4. [23] 丁力平,谭建荣,冯毅雄,等. 基于Pareto 蚁群算法的拆卸线平衡多目标优化[J]. 计算机集成制造系统,2009, 15(7):1406-1413,1429. Ding L P, Tan J R, Feng Y X, et al. Multiobjective optimization for disassembly line balancing based on Pareto ant colony algorithm[J].Computer Integrated Manufacturing Systems,2009, 15(7):1406-1413,1429. [24] Mora A M, Merelo J J, Castillo P A, et al. A study of parallel approaches in MOACOs for solving the bicriteria TSP[M]∥Advances in computational intelligence.New York: Springer, 2011, 6692:316-324. [25] Ellabib I, Calamai P, Basir O. Exchange strategies for multiple ant colony system[J].Information Sciences, 2007, 177(5): 1248-1264. [26] Twomey C, Stützle T, Dorigo M, et al. An analysis of communication policies for homogeneous multi-colony ACO algorithms[J]. Information Sciences, 2010, 180 (12):2390-2404. [27] Jovanovic R, Tuba M, Simian D. Comparison of different topologies for island-based multi-colony ant algorithms for the minimum weight vertex cover problem[J]. IEEE Transactions on Computers, 2010, 9(1):83-92. [28] Xiong J, Liu C Y, Chen Z. A new parallel ant colony optimization algorithm based on message passing interface[C]∥Pacific-Asia workshop on computational intelligence and industrial application(PACIIA08).Wuhan, China,2008:178-182. [29] Yu B, Yang Z Z, Xie J X. A parallel improved ant colony optimization for multi-depot vehicle routing problem[J]. Journal of the Operational Research Society, 2011, 62: 183-188. [30] Bilchev G, Parmee I C. The ant colony metaphor for searching continuous design spaces[M]∥Evolutionary computing.New York: Springer, 1995, 993:25-39. [31] Lee Z J, Su S F, Chuang C C, et al. Genetic algorithm with ant colony optimization (GA-ACO)for multiple sequence alignment[J]. Applied Soft Computing, 2008, 8(1):55-78. [32] Thanushkodi K, Deeba K. Hybrid intelligent algorithm[improved particle swarm optimization (PSO) with ant colony optimization (ACO)] for multiprocessor job scheduling[J].Scientific Research and Essays,2012, 7(20): 1935-1953. [33] Liu D H, Chen G P. A new method for multi-objective optimization problem based on multi-ant-colony algorithm[C]∥International conference on computer application and system modeling(ICCASM10).Taiyuan,China. 2010: V7605-V7609. [34] Chica M, Cordón O, Damas S, et al. A new diversity induction mechanism for a multi-objective ant colony algorithm to solve a real-world time and space assembly line balancing problem[J].Memetic Computing, 2011, 3(1): 15-24. [35] Middendorf M, Reischle F,Schemeck H. Multi colony ant algorithms[J]. Journal of Heuristics, 2002, 8(3): 305-320. [36] Bezerra L C T, Goldbarg E F G, Buriol L S, et al. GRACE: A generational randomized ACO for the multi-objective shortest path problem[J].Lecture Notes in Computer Science, 2011, 6576: 535-549. [37] Raith A, Ehrgott M. A comparison of solution strategies for the biobjective shortest path problem[J].Computers & Operations Research, 2009, 36(4): 1299-1331. [38] Bezerra L C T, Goldbarg E F G, Goldbarg M C, et al. Analyzing the impact of MOACO components: An algorithmic studyon the multi-objective shortest path problem[J]. Expert Systems with Applications, 2013, 40(1): 345-355. [39] Alaya I. Ant colony optimization for multi-objective optimization problems[C]∥IEEE international conference on tools with artificial intelligence (ICTAI10). Patras, Greece, 2010:450-457.

2 求解多目标蚁群优化的新型范例研究
2.1 基于分解的多目标蚁群优化
2.2 基于种群的多目标蚁群优化
2.3 基于Pareto最优的蚁群优化
3 多目标蚁群算法的并行化
4 多目标蚁群算法的发展展望
