先锋-顶级种群反应扩散模型的平衡点线性稳定性

曹佳敏, 温俊浩, 翁佩萱

(华南师范大学数学科学学院,广州 510631)

在生物圈中,不同的种群有着不同的特性描述.“先锋种群”是指在种群密度较低时生长旺盛,随着种群密度的不断增加,竞争加剧而导致生长缓慢的一类种群,其适应度函数在种群密度较低时取得最大值,随着种群密度的不断增加而持续单调下降,该种群的适应度函数只有唯一的零点.在自然界中这个种群扮演的是“拓荒者”的角色.例如：松树、北美鹅掌楸等就是符合这种生长规律的物种.“顶级种群”是另一类种群,它在种群密度较低或较高时,相应的适应度函数的值均小于零,而其适应度函数的最大值一般在适应度函数的2个零点之间取得.满足这种生产规律的物种有:橡树、枫树等.

研究多个物种之间相互作用的动力学规律是生物数学的重要目标.一般说来,种群之间相互作用的动力学模型是以一个微分系统呈现的. 如果在考虑时间因素和种群相互作用的同时也考虑种群在空间的扩散, 那么常见的一类模型是反应扩散方程, 更详细的介绍可见文献[1]、[2]. 本文研究的是如下关于先锋种群和顶级种群相互作用的反应扩散方程:

对系统(1)进行无量纲化,可以得到:

根据前面的描述, 先锋种群和顶级种群的适应度函数f和g具有以下性质：

(i)f′(z)<0且存在唯一的z0>0, 使得f(z0)=0.

相应的图像可以参考图1. 我们可以举出一些满足性质(i)和(ii)的适应度函数例子[3-5],例如：f(u)=er(1-u)-a,g(u)=uer(1-u)-a.

图1 先锋种群和顶级种群的适应度函数图像

如果不考虑空间扩散因素,则这个系统对应于一个常微分方程组,其平衡解的稳定性与Hopf分支已有较多研究[6-8]. 就我们所知,对于反应扩散系统(1),文献[3]、[9]就平衡点处可能出现Hopf分支进行了讨论,文献[8]讨论了系统(1)的图灵不稳定性. 但是,系统(2)的平衡态稳定性问题尚未有文献全面讨论. 受文献[10]、[11]的方法启发,本文主要研究系统(2)在所有平衡点处的线性稳定性.

1 系统平衡点分析

其次,可以看出,除了上面的4个平衡点,其他的可能平衡点可以通过求解以下方程组得到:

容易得到方程组(3)、(4)分别有解：

由于生物意义,我们只关注系统的共存平衡点,即满足u+>0,v+>0的正平衡点(u+,v+). 也就是说,只关注本身是正平衡点的(u1,v1)和(u2,v2). 通过分析c11u+v=z0,u+c22v=w1,u+c22v=w2这3条直线的位置关系,可以把系统(2)存在平衡的情况分为如下4类(包括9种子情形. 具体的讨论类似于没有扩散的常微分系统,可参考文献[12], 这里略去):

(1)在如下任何一组条件下,系统(2)只有4个边界平衡点, 没有共存平衡点:

(2)在如下任何一组条件下,系统(2)有4个边界平衡点和1个共生平衡点(u2,v2):

(3)在以下任何一组条件下,系统(2)有4个边界平衡点和1个共生平衡点(u1,v1):

(4)在以下任何一组条件下,系统(2)有4个边界平衡点和2个共生平衡点(u1,v1)和(u2,v2):

2 平衡点的线性稳定性

我们将讨论系统(2)各个平衡点的线性稳定性. 首先,假设(u0,v0)是系统的任意一个平衡点, 把系统(2)在(u0,v0)点处线性化得到线性化系统：

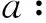
考虑线性方程(6)形如

方程(8)具有非零解当且仅当以下行列式为零成立:

其中

A(,σ,u0,v0)=+d1σ2-f(a)-c11u0f′(a),

B(,σ,u0,v0)=+d2σ2-g(b)-c22v0g′(b),

整理上面的式子,可以得到特征方程:

A(,σ,u0,v0)B(,σ,u0,v0)-u0v0f′(a)g′(b)=0.

(9)

下面将依据方程(9)的特征根分布情况来讨论系统各个平衡点的线性稳定性.

定理1 (0,0)点为线性不稳定的.

证明取(u0,v0)=(0,0), 这时a=0,b=0, 代入方程(9)得(+d1σ2-f(0))(+d2σ2-g(0))=0.由f的性质知f(0)>0,从而可以取σ>0充分小使得=-d1σ2+f(0)>0, 即存在正的特征根, 故(0,0)为线性不稳定的. 证毕.

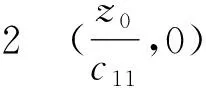
(+d1σ2-z0f′(z0))(

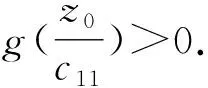
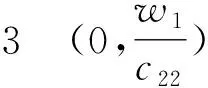
(+d2σ2-w1g′(w1))=0.

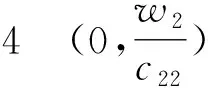
(+d2σ2-w2g′(w2))=0.

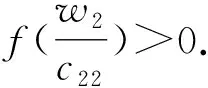
定理5 在子情形(2b)、(4b)下,正平衡点(u2,v2)为线性渐近稳定的;在子情形(2a)、(4a)下，(u2,v2)为线性不稳定的.

证明取(u0,v0)=(u2,v2),有a=z0,b=w2, 代入方程(9)得:

u2v2f′(z0)g′(w2)=0.

(10)

令α=α(σ)和β=β(σ)如下：

d1c22v2g′(w2))σ2+(c11c22-1)u2v2f′(z0)g′(w2).

由于f′(z0)<0,g′(w2)<0,可得

Δ=α2-4β=[(d1+d2)σ2-(c11u2f′(z0)+

c22v2g′(w2))]2-4[d1d2σ4-(d2c11u2f′(z0)+

d1c22v2g′(w2))σ2+(c11c22-1)u2v2f′(z0)g′(w2)]=

(d1-d2)2σ4+2(d2-d1)σ2(c11u2f′(z0)-

c22v2g′(w2))+(c11u2f′(z0)-c22v2g′(w2))2+

4u2v2f′(z0)g′(w2)=[(d1-d2)σ2-(c11u2f′(z0)-

c22v2g′(w2))]2+4u2v2f′(z0)g′(w2)>0.

(11)

首先考虑子情形(2b)和(4b), 这时c11c22>1. 由于f′(z0)<0,g′(w2)<0, 故对任意σ, 总有α>0,β>0.由一元二次方程的求根公式可知2+α+β=0的根均为负数,从而(u2,v2)点为线性渐近稳定的.

其次考虑子情形(2a)和 (4a), 这时有c11c22<1, 同样地有α>0.当σ=0 时,β=β(0)=(c11c22-1)u2v2f′(z0)g′(w2)<0.此时方程的根为一正一负, 故总可以找到σ使得方程有正根, 从而(u2,v2)点为线性不稳定的. 证毕.

从第1节可知平衡点(u1,v1)在子情形(3a)、(3b)、(4a)、(4b)下出现. 为了讨论平衡点(u1,v1)的稳定性,取(u0,v0)=(u1,v1),有a=z0,b=w1, 代入式(9)得:

u1v1f′(z0)g′(w1)=0.

(12)

令p=p(σ)和q=q(σ)如下：

那么,式(12)被整理为等价形式

2+p+q=0.

(14)

方程(14)的根的判别式记为Δ(σ),则可以算出类似于式(11)的计算,只要把其中的g′(w2)换成g′(w1), 即可得到Δ=Δ(σ)的公式：

c22v1g′(w1))]2-4[d1d2σ4-(d2c11u1f′(z0)+

d1c22v1g′(w1))σ2+(c11c22-1)u1v1f′(z0)g′(w1)]=

[(d1-d2)σ2-(c11u1f′(z0)-c22v1g′(w1))]2+

4u1v1f′(z0)g′(w1).

(15)

下面2个定理的讨论都将依据特征方程(14)的根的实部符号来阐述平衡点(u1,v1)的线性稳定性.

定理6 在子情形(3b)、(4b)下,正平衡点(u1,v1)为线性不稳定的.

证明在子情形(3b)、(4b)下,有c11c22>1. 则

Δ(0)=(c11u1f′(z0)-c22v1g′(w1))2+

4u1v1f′(z0)g′(w1)=(c11u1|f′(z0)|+

c22v1g′(w1))2-4u1v1|f′(z0)|g′(w1)=

(c11u1|f′(z0)|)2+(c22v1g′(w1))2+

2c11c22u1v1|f′(z0)|g′(w1)-4u1v1|f′(z0)|g′(w1)≥

4(c11c22-1)u1v1|f′(z0)|g′(w1)> 0.

另一方面, 有

q(0)=(c11c22-1)u1v1f′(z0)g′(w1)<0.

无论p(0)为任何实数,根据一元二次方程的求根公式,方程2+p(0)+q(0)=0的根总是一正一负. 也就是说,在子情形(3b)、(4b)下,总可以找到σ使得方程2+p+q=0有正根,从而(u1,v1)为线性不稳定的. 证毕.

为了在下面的定理中讨论子情形(3a)和(4a), 我们先做一些准备工作. 注意这时有c11c22<1.为了方便讨论,引进一些记号. 令

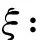
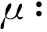
显然有ξ≥0,ζ>0,μ<0,ν<0,γ>0.

根据以上定义给出下面的引理.

引理1 在子情形(3a)、(4a)下,以下结论成立：

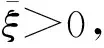
(w1)当θ>0 时,η>(d1-d2)ζ;

(w2)当θ=0 时,η=(d1-d2)ζ;

(w3)当θ<0 时,η<(d1-d2)ζ.

把这些记号代入式(13)和式(15)中得到:

p(ξ)=(d1+d2)ξ-θ,q(ξ)=d1d2ξ2-ηξ+γ,

Δ(ξ)=[(d1-d2)ξ-μ]2+ν=

(d1-d2)2ξ2+2(d2-d1)μξ+μ2+ν.

先分析p(ξ)=0. 由于p′(ξ)=d1+d2>0, 那么对∀ξ≥0有p(ξ)单调递增,对p(ξ)有:

(p1)当θ<0 时,对∀ξ≥0有p(ξ)>0;

(p2)当θ=0 时,对∀ξ≥0有p(ξ)≥0;

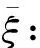
最后分析q(ξ)=0,即

d1d2ξ2-ηξ+γ=0.

(16)

我们分以下4种情况来分析：

显然在[0,ξ1)∪(ξ2,+∞)上有q(ξ)>0, 在(ξ1,ξ2)上有q(ξ)<0.

定理7 在子情形(3a)、(4a)下, 如果满足下列条件之一：

(1)d1≤d2,θ<0;

则(u1,v1)为线性渐近稳定的.

证明由θ<0和(p1)推知:在定理的任何一个条件下,总有p(ξ)>0对ξ≥0.

先证明在条件(1)下(u1,v1)为线性渐近稳定的. 由d1≤d2,θ<0 和(w3)推知η<0, 从而由(q4)推知q(ξ)>0对ξ≥0.由方程(13)和一元二次方程的求根公式知道:当Δ>0时,方程(13)的根为两负根; 当Δ=0时,方程(13)的根为1,2=-p/2;当Δ< 0时,方程(13)有一对共轭复根具有负实部, 故(u1,v1)为线性渐近稳定的.

证毕.

定理8 在子情形(3a)、(4a)下, 如果满足下列条件之一：

(1)θ>0;

则(u1,v1)为线性不稳定的.

注1 注意定理7中的条件(1)和(w2)、(w3)推出η≤(d1-d2)ζ≤0, 这时定理8中的条件(1)、(2)自然都不成立.也就是说,定理7中的任何一组条件都是同时否定定理8中的条件(1)、(2)的.

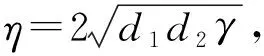
3 数值模拟

考虑如下模型：

显然,系统(17)中f(z)=z0-z,g(w)=-(w1-w)×(w2-w).通过计算得f′(z0)=-1,g′(w1)=w2-w1>0,g′(w2)=w1-w2<0,g′(w*)=0, 这里w2>w1>0,w*=(w1+w2)/2.

首先考虑子情形(3a),下面总取

将式(18)代入系统(17)有

经过计算得(u1,v1)=(4/3,1/3).

系统(19)在(u1,v1)=(4/3,1/3)处的线性化方程为

取d1=1,d2=1/2, 此时θ=-5/12,η=-1/12,γ=1/2,显然满足定理7中的条件(2),这时有(u1,v1)=(4/3,1/3)是线性渐近稳定的,模拟结果见图2.

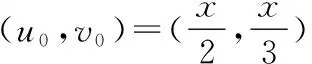
对于原系统(19)，仍然取d1=1,d2=1/2,此时根据模拟的结果(图3),我们猜测(u1,v1)=(4/3,1/3)为局部渐近稳定的.

这一节只给出了定理7中子情形(3a)下条件(2)的数值模拟,对于定理7中子情形(3a)下的条件(1),我们只需随意取定一组d1、d2,满足0≤d1≤d2,其余的参数如式(18)所取,对于定理7中子情形(4a)的讨论只需取z0=1,w1=3/2,w2=2,c11=1/4,c22=1/2.而d1,d2同子情形(3a)下的取法,均可以进行数值模拟,将不再赘述.

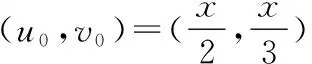
参考文献：

[1] Shigesada N, Kawasaki K. Biology invasions: Theory and practice[M]. Oxford: Oxford University Press, 1997.

[2] Murray J D. Mathematical biology: I, II[M]. New York: Spriner-Verlag, 2002.

[3] Selgrade J F, Namkong G. Stable periodic behavior in a pioneer-climax models[J]. Nature Resource Modeling, 1990, 4:215-227.

[4] Ricker W E. Stock and recruitment[J]. Journal of the Fisheries Research Board of Canada, 1954, 11:559-623.

[5] Franke J E, Yakubu A A. Pioneer exclusion in a one-hump discrete pioneer-climax competing system[J]. Journal of Mathematical Biology, 1994,32: 771-787.

[6] Summer S. Hopf bifurcation in pioneer-climax species models[J].Mathematical Biosciences, 1996, 137: 1-24.

[7] Summer S. Stable periodic behavior in pioneer-climax competing species models with constant rate forcing[J]. Nature Resource Modeling, 1998,11: 155-171.

[8] Buchanan J R. Turning instability in pioneer-climax species interactions[J]. Mathematical Biosciences, 2005, 194: 126-199.

[9] Liu J X, Wei J J. Bifurcation analysis of a diffusive model of pioneer and climax species interaction[J]. Advance in Difference Equation, 2001, 24: 11-52.

[10] 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京：科学出版社, 2004.

[11] 吴敏, 翁佩萱. 具有阶段结构的多时滞SIR扩散模型的稳定性[J]. 华南师范大学学报:自然科学版, 2013, 45(2): 20-23.

Wu M, Weng P X. Stability of a stage-structured diffusive SIR model with delays[J]. Journal of South China Normal University: Nature Science Edition, 2013, 45(2): 20-23.

[12] Buchanan J R. Asymptotic behavior of two interacting pioneer-climax species[J].Fields Institute Communication, 1999, 21: 51-63.