运输问题的表上作业法中初始方案的优化

2014-08-28张晓瑾刘海生

华北科技学院学报 2014年6期

张晓瑾，刘海生

(华北科技学院基础部，北京东燕郊 101601)

0 引言

运输问题是特殊的线性规划问题，表上作业法是运用了单纯形法的原理，结合运输问题自身的特点，而得到的一种求解产销平衡运输问题的简便而有效的方法。但在其迭代计算过程中，其初始方案的确定、检验和方案的调整改进处理不一样时，计算工作量大相径庭。如何才能减少迭代次数，用最少的工作量来求得最优方案，本文对表上作业法中初始方案的确定进行了一定的思考和改进。

对于产销平衡运输问题初始方案的确定，常用的方法有三种:最小元素法、西北角法和Vogel法。一般地，Vogel法确定的初始方案质量最好，最接近最优解;最小元素法次之;西北角法最差。本文重点研究利用Vogel法确定初始方案过程中存在的不足和改进的工作。

1 方法存在的问题

用Vogel法确定初始方案时，其过程中出现的问题:

1)当一次计算中出现最大罚数有2个及2个以上时，究竟选取哪一个罚数对应的行或列来填数字，选取不当时，后期迭代步骤不同，初始方案质量不同。针对此问题，教材［7］中以及相关文献中未做出明确的说明。

2)在Vogel法确定初始方案过程中出现退化解时，如何确定填“0”的位置。先后有多篇文章讨论过这个问题，如［1］－［6］。在文献［1］中指出:“填到数字格所在行或所在列的未划去或未填数字格中单位运价最小的位置，可以避免可能存在的多余的计算。”实践表明，这一说法不完善。例如表1(表中“()”中为检验数;“○”中为初始方案，下表中相同).

表1 产销平衡运输表

在A3B1位置填入数字2时，供销关系同时得到满足，此时有四个位置 A1B1，A2B1，A3B2和 A3B3可以填0。而单位运价最小者为位置A3B2，选其位置填0，得到初始方案，并计算其检验数见表1。空格位置A3B3检验数小于零，当前方案不是最优方案(见表1)。而如果选择将0填入位置A3B3，计算得到其初始方案和检验数见表2。此时，所有检验数都大于零，得到的初始方案为最优方案。故选择填到“数字格所在行或所在列的未划去或未填数字格中单位运价最小的位置”，这一说法未必能减少迭代次数。

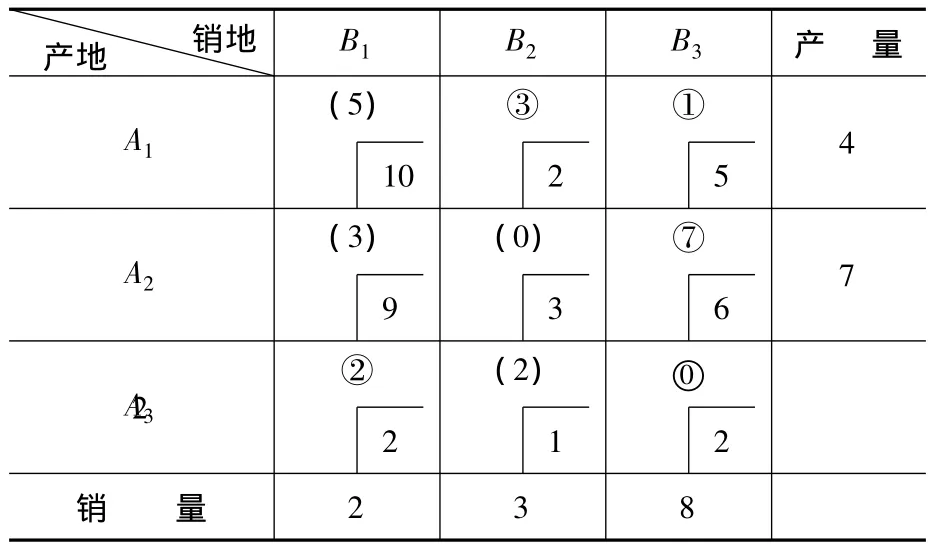
表2 产销平衡运输表

下面针对以上两个问题，谈谈本文的改进工作:

2 方法的补充和改进

1)用Vogel法确定初始方案时，当一次计算中最大罚数有2个及2个以上时，可以改进提高初始方案的质量。

在理论上，由任意最大罚数所在行或所在列的最小运价确定数字格均可。但是，当最大罚数所在行或所在列的各最小单位运价不等时，选取最大罚数对应的不同的行或列，初始调运方案质量就不一样，迭代次数也不同。实践证明:由最大罚数所在行或所在列的各最小单位运价的最小者，确定数字格而获得的初始方案质量好。而且当产地和销地较少时，有时得到的初始方案就是最优方案。例如表3中的产销平衡问题。

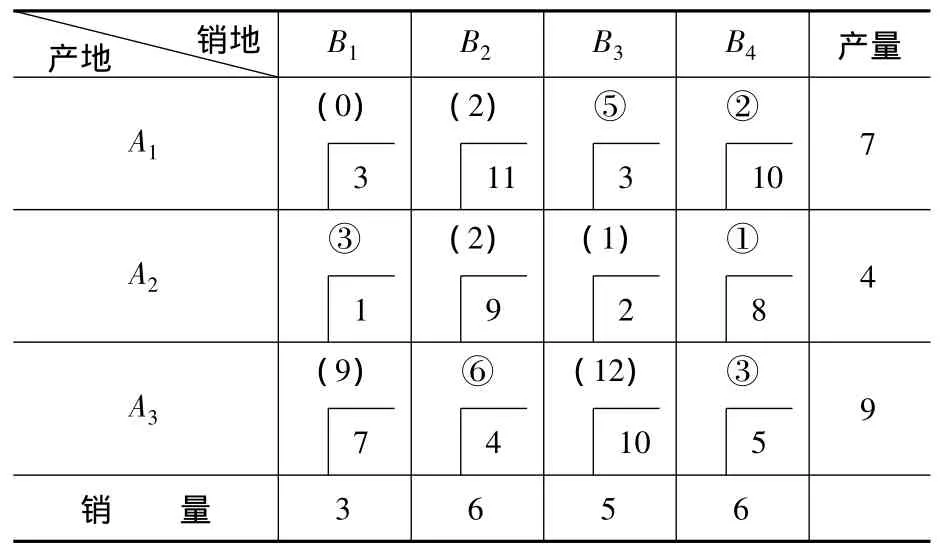
表3 产销平衡运输表

在利用Vogel法确定初始方案，填A2B1时，遵从这一规则:有相同最大罚数为2，选取了罚数为2的所在行和列中未被划去的行和列中单位运价最小的位置A2B1，优先得到满足。方案确定后，经检验其方案为最优(见表3)。

2)用Vogel法确定初始方案，在填数字格时，若同时满足其所在行和所在列的供销关系，需选择某一位置填“0”，此时出现退化解。填“0”的位置不同，由此而获得初始方案的质量不一样，后期迭代次数也不一样。

下面从客观上分析此问题:在书［7］中明确指出“通过任一空格可以找到，并且只能找到唯一的闭回路，并由此计算出全部空格处的检验数”。据此任一空格位置检验数的正负，唯一取决于闭回路各个拐点处数字格单位运价数值的相对大小。由于具体不同问题中各个单位运价之间没有必然的关联，客观上导致检验数计算结果的正负随机性，填“0”位置没有一个统一的规律。于是想从填“0”这方面减少迭代的次数，没有一个统一的规则。

虽然如此，我们还是可以从两方面着手去优化Vogel法确定初始方案:

一方面，通过后期观察法选取填“0”位置，减少空格位置检验数出现负值的可能性。

下面举例说明，具体步骤如下:

第一步:计算行和列的罚数，确定出第一个数字格。销地B1对应罚数为最大，其值为8;选择在A3B1位置填入数字5时。此时供销关系同时得到满足，划去第3行和第1列，需选某一位置填0。有 A1B1，A2B1，A3B2，A3B3和A3B4对应的5个位置可以填0，具体位置待定(见表4)。

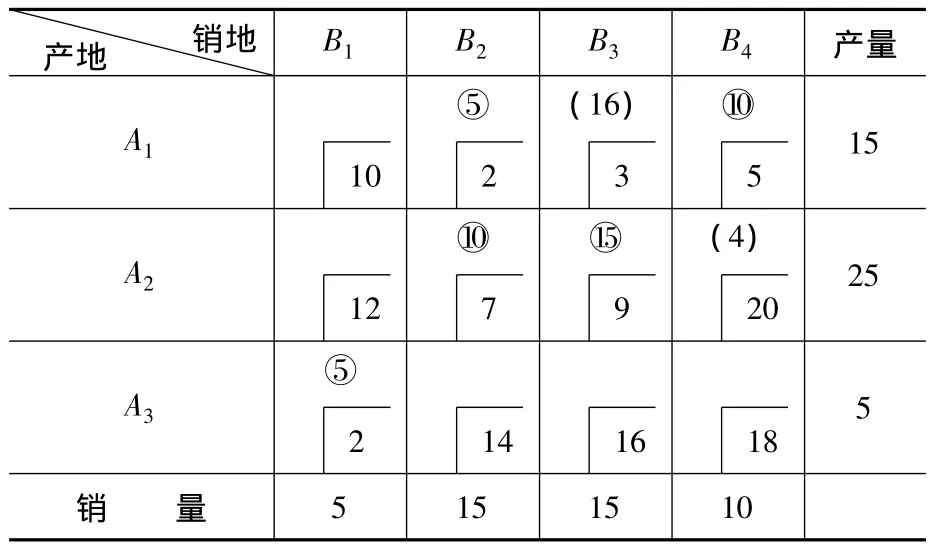
表4 产销平衡运输表

第二步:视A3B1所在行和列已划去，依据第一步中的规则，继续确定出其它位置的数字格(见表4)。

第三步:依据当前5个数字格，利用闭回路法确定出部分空格的检验数(见表4)。

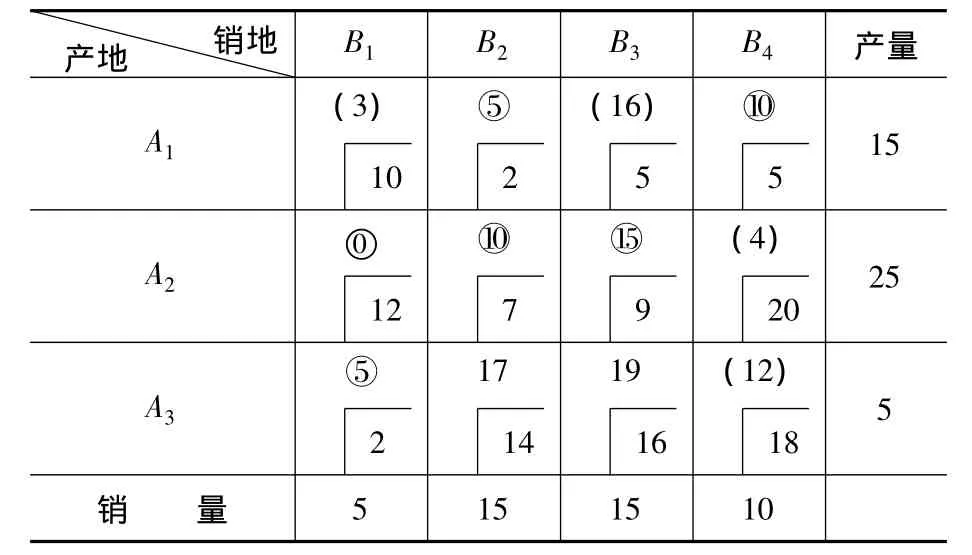
表5 产销平衡运输表

第四步:填“0”的位置影响其它空格位置检验数的正负，通过位置筛选法，选择某一位置填0。从5个位置中选择一个填0，具体作法:当A1B1位置填0时，观察与之相关的空格，发现其在A2B1对应闭回路中，空格A2B1检验数12－7+2－10=－3＜0，放弃此位置;同理当A3B2位置填0时，发现其在A3B4对应闭回路中，空格A3B4的检验数18－14+7－20= －9＜0，放弃此位置;据此适当排除一些位置，一定程度上提高初始方案的质量，减少迭代次数，见表5。

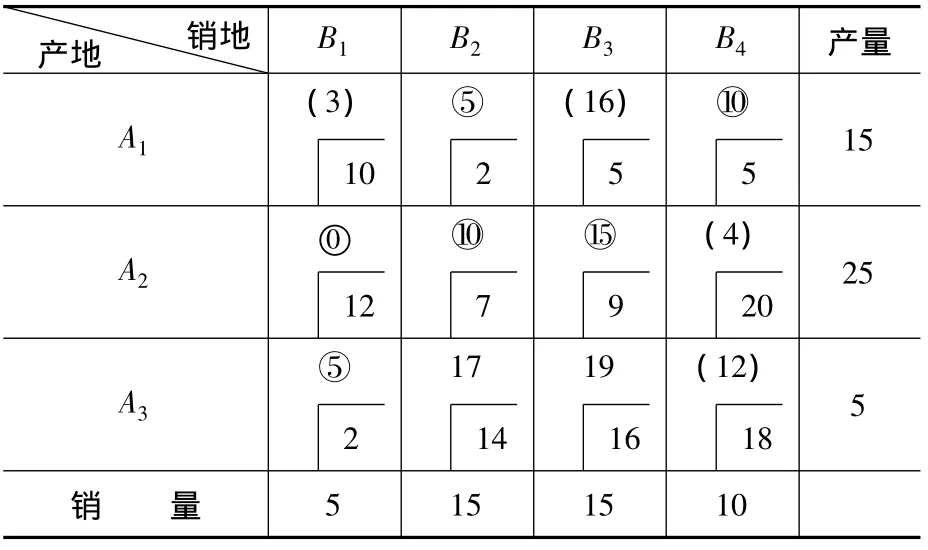
表5 产销平衡运输表

当产销平衡的运输问题中产地和销地数相对较少时，此法效果很好。当产地和销地比较多时，试图通过后期观察法填“0”，实现初始方案的优化，减少迭代次数已经不易操作。

另一方面，在符合条件的任意位置填“0”，依据检验数为负的空格调整量来判断，实现优化。具体作法是:运用Vogel法确定出初始方案，当出现一个空格处检验数为负时，运用闭回路法进行调整;若调整量为0时，结合文献［6］的说明，文献［2］中判别方法，可知此时已经得到最优方案，无需继续迭代。若调整量不为0时，说明当前方案不是最优方案，运用闭回路法调整方案，继续迭代寻找最优方案;当出现多个空格处检验数均为负值但调整量都为0时，结合［2］可知，此时已经得到最优解;否则闭回路调整方案。此方法对于检验数为负值且调整量为0的情形，大大减少了方案迭代的次数，优化了初始方案。