错题是个宝 千万要用好
——一道高考模拟题的错解分析与实验验证
2014-08-28
(江苏省海门市三厂中学,江苏 海门 226121)
学生在考试或作业中做错题目,是中学物理教学中司空见惯的现象,它反映了学生的“学”和教师的“教”中存在的问题.俗话说:“吃一堑,长一智.”错误是正确的先导,只要我们善于总结错题,利用好错题这个宝贝资源,在物理复习中一定会起到事半功倍的效果.本文笔者以一道模拟考试中的错题为例,谈谈如何利用学生的错题资源,提高复习的效率.
1 原题
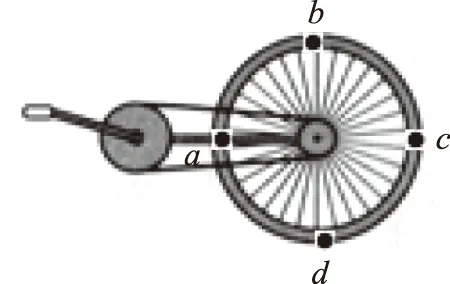
图1
(2014年南京、盐城一模第5题)如图1所示为自行车的传动机构,行驶时与地面不打滑.a、c为与车轴等高的轮胎上的两点,d为轮胎与地面的接触点,b为轮胎上的最高点.行驶过程中( ).
A.c处角速度最大
B.a处速度方向竖直向下
C.b处向心加速度指向d
D.a、b、c、d四处速度大小相等
答案为C.
2 答题基本情况
我校一个选修物理和化学的普通班,参考总人数为45人,其各个选项的答题情况如表1所示.
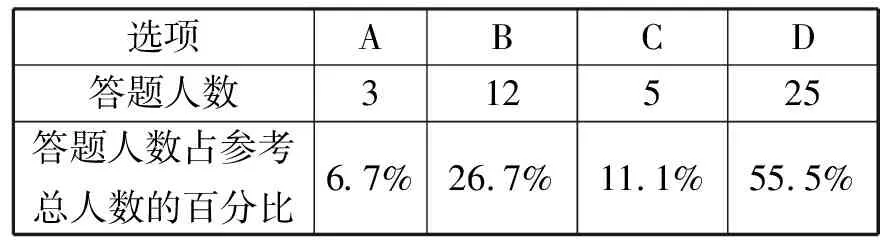
表1
由表1数据可知:本题答对的人数仅占班级参考总人数的1/9,绝大多数同学错选了选项B或选项D,极个别同学错选了选项A.因此本题实属单选题中较难的一题.
3 错解分析
自行车在正常往前行驶时,车轮边缘上的每一点实际上参与了两个分运动:一是车轮绕车轴的转动,二是和车轴连同车架一起向前的平动.这两个分运动合成的结果就造成了车轮的上半部分和下半部分的转动不一样快.如图2所示,在车轮的上半部分,车轮旋转运动的方向和车子向前平动的方向是一致的,两者速度应相加;而在车轮的下半部分,车轮旋转运动的方向和车子向前平动的方向正好是相反的,两者速度则相减.因此从地面上静止的观察者来看,车子的上半部分就要比下半部分移动的快一些.这与自行车停在地面上,车轮空转时的情况是不同的.自行车停在地面上,车轮空转时,车轮边缘上任意一点只有绕中心轴的转动,而无随车轴一起向前的平动.因此相对地面,车轮边缘各点移动的快慢程度都是一样的.

图2
错选B的同学忽视了车轮的向前平动,a点的速度应该是两个分速度的合成(如图2所示),方向肯定不是竖直向下的,而是偏向前下方.错选D的同学也同样只注意到了车轮的转动,错误地认为车轮边缘上各点的速度大小都相等,而忽视了跟随车轴一起向前的平动.同样的道理,c点也肯定不是角速度最大的点,故选项A错误.本题的正确答案应该是选项C,因为此时在车轮的最高点b处,车轮绕轴转动的速度和向前平动的速度方向相同,叠加后合速度的大小最大,方向水平向左.根据转动的原理,向心加速度的方向与线速度的方向垂直,所以b处的向心加速度方向应竖直向下,指向d点.
4 课堂定性实验验证
经过以上理论分析,绝大多数原来做错的学生认识到了自己当初的错误,明白了车轮上、下两部分其实转动不一样快的原理.但仍有少部分学生还是将信将疑,认为明明是同一个车轮上的转动,为什么转动的速度又不一样呢?
于是笔者在课堂上设计了一个简单的实验,定性验证了上述结论.我们用一个铁丝弯成一个圆环当做自行车的车轮,并用一根直尺恰好通过竖直圆环的圆心,在直尺对准的圆环边缘的最上端和最下端分别做一个标记A和B,如图3所示,将圆环稍微向前滚动,这时就会发现上端的A移动了较大的一段距离到达了A′,而下端的B却只离开原来的位置很小的一段距离BB′.由此可见上端的A点要比下端的B点移动的速度明显要大得多.

图3
5 课后实际观察验证
课堂上的定性小实验虽然可以直观地理解为什么车轮上半部分转动的速度要比下半部分的快,但这个实验毕竟是抽象的,与实际生活中见到的情况相差很大.于是笔者在课后带领同学们到马路边观察和记录了一个真实的车轮转动情况.
我们将数码相机固定在三脚架上,镜头对准车辆轮胎可能经过的地方,锁定好焦距,将数码相机设置成“快门优先”,曝光时间设置为1/200秒.一切准备就绪后,静静地等待车辆驶过.当一辆卡车急速驶过时,我们快速按下快门,使用相机的连拍功能拍了3张照片.我们挑选了一张画面比较完整且清晰的照片进行观察,如图4所示.从这张照片上我们可以清楚地看到,卡车车轮的上半部分比较模糊,几乎连成一片,而下半部分,特别是靠近地面的地方可以清晰分辨出轮胎的齿纹.这个现象正好说明了行驶中的车轮上半部分要比下半部分转动得快的道理.

图4
6 延伸巩固练习
一辆汽车以20m/s的速度水平匀速行驶,(1)若以车轴为参考系,车轮轮缘上各点的速度是多大?(2)若以地面为参考系,车轮上的a、b、c、d各点的速度又分别是多大?

我们说失败是美丽的,错误是精彩的,问题的关键在于如何把失败和错误变成我们有用的资源.我们要善于挖掘和发挥错题的功能,提高错题的价值,从而达到让学生减少出错的目的.
