Peirce机织物几何结构模型的探讨

郑天勇，吴 珍，赵媛媛，李婷婷

(河南省功能性纺织材料及应用重点实验室 中原工学院，河南 郑州451191)

机织物中经纬纱线交织的空间形态关系称为机织物几何结构(以下简称为织物结构).在织造过程中，由于经纬纱线的黏弹性、上机张力及织物组织、密度等的不同，使经纬纱之间形成各种各样的屈曲配合关系，形成了经纬纱空间形态比较复杂的织物.织物几何结构的定性描述，对研究织物的风格评价、力学性能、通透性、耐磨性、尺寸稳定性及织物能达到的最大可织密度具有很大的作用.1937年，Peirce［1］率先提出了一种机织物几何结构模型并给出一系列计算公式，Kemp［2］和Hearle等［3］在其基础上对Peirce模型进行了修正.由于织物织造缩率影响结构的计算结果，吴汉金等［4］提出了各类织物织造缩率的经验估计.在这些研究中，对数据的验证是根据织物切片实验进行的.

近年来，一些基于Peirce几何结构模型的机织物CAD系统模拟的织物结构与真实织物结构相差较大，其根源应该是织物结构的计算精度不高，故探讨Peirce机织物几何结构模型的准确性很有必要.

1 Peirce机织物几何模型

在Peirce机织物结构模型中，假定织物中经纬纱的横截面均为圆形，纱线既无伸长也无压缩变形，同一浮长包覆下的纱线在同一水平面上，即经纱和纬纱紧密接触(可能有压缩)，纱线在经纬纱交织附近相互包覆屈曲的地方为圆弧状，其余部分为直线段.建立了一系列的关于纱线的屈曲长度、波高、几何密度、直径、缩率与交织角的关系式，来近似说明机织物中经纬纱屈曲波高无论怎样变化，其和为一个常数，等于经纬纱直径之和乘以压扁系数，即

织物结构的屈曲波高计算公式通过简化，可写成如下形式:

式中，h表示纱线屈曲波高，d表示纱线直径，C表示织造缩率，ρ表示纱线之间的间距，R是组织循环根数，t是交错数，下标j和w分别表示经纱和纬纱，系数k是一个常数.当屈曲形态为正弦线时k=1.273，为抛物线时k=1.256，在圆弧结合直线时k=1.333.

2 经典教材小浮长织物实例检验

当浮长较小(为1或2)时，经纬纱基本紧密接触，在理论上平纹织物应满足上述公式.然而，以顾平编写的《织物组织与结构学》［5］中一个平纹织物几何结构相计算实例为例，某平纹丝织物的经纬丝均采用55 dtex涤纶丝，经密ρj=80根/cm，纬密ρw=55根/cm，经丝织造缩率Cj=12%，纬丝织造缩率Cw=7%，试计算其经纬丝的屈曲波高和交织角.按照Peirce模型的近似式求解，过程如下:

式中，δ为纱线的密度，g/cm3，涤纶丝δ取1.38 g/cm3;Nt为纱线的特数.

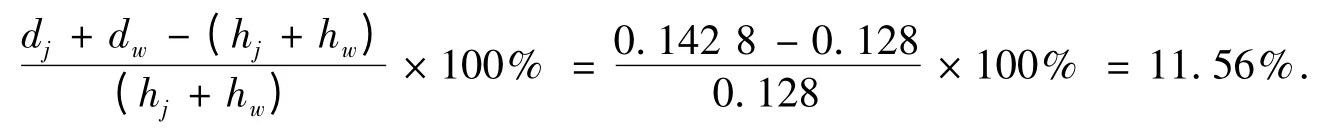
根据计算结果，误差约为11.56%.若k=1.256，误差将达到19%，误差值使人难以接受.

考虑到纱线在织物中被压扁这一实际情况，提出了压扁系数η的概念，取值一般为0.60～0.80，有的可以达到0.85，公式(1)变为公式(4):

虽然压扁系数的提出在一定程度上使Peirce公式能够得到满足，但由于其变化范围过于宽广，仅系数的误差就达到40%以上，显然计算结果差异会很大.

在蔡陛霞编写的《织物结构与设计》［6］中，列举了本色原棉布织物规格的参考表，分别计算其屈曲波高和理论直径(k=1.333)，可知按Peirce模型的近似式所计算的经纬纱屈曲波高值与经纬纱理论直径和之间存在较大差异，压扁系数的变化范围也太大，对于织物结构的计算没有实际意义.误差出现负值，说明屈曲波高之和大于经纬纱直径之和，纱线肯定有压扁情况，但是计算时没有意义，只会导致计算误差更大.有时由于误差巨大，比如超过100%，即使考虑压扁系数，公式(4)也无法接受.

3 长浮长织物的直观验证

在机织物组织中，浮长越短，交织次数越多;浮长越长，交织次数越少.当浮长线大于3时，对各种织物进行分析，发现某系统纱线上的浮长越长，其本身可能的凸起或凹下程度越高，浮长中部离织物的中心线越远［7］，即屈曲波高会随着浮长的变化而变化.浮长大到一定程度时，经纬纱就不一定能接触.正常织物中纱线在应力作用下有收缩的趋势，使被浮长线覆盖并拉拢的另一系统的若干纱线距离缩小甚至紧密接触，长浮长的中间组织点受两侧的挤压力大致均衡，位置基本保持不动，同浮长内的其他组织点向中央靠拢.在多重组织和多层组织中，纱线在挤压下容易重叠.在有些单层组织中，长浮长线与其相邻短浮长之间，浮长相差悬殊，在另一系统的浮长线拉拢之下使相邻距离的几根纱线形成局部重叠，织造效果如图1和图2所示，组织点凸起或者凹下，纱线不在同一个平面上.由于经纬纱直径是恒定值，显然公式(1)或公式(4)将不成立，即对于长浮长机织物，Peirce模型不再适用.

图1 透孔组织显微镜镜图Fig.1 Magnified photos for mock leno woven structure

图2 蜂巢组织显微镜镜图Fig.2 Magnified photo for honeycomb woven structure

4 混合规律的织物几何结构验证

4.1 样品设计与织造

通过研究在组织不同而其他条件相同时浮长线变化对同一块机织物中屈曲波高的影响，来判定Peirce公式的适用性.本研究采用Nedgraphics Jacquard系统设计了一块组织规律呈正交型或包围圈型分布的纹样图，织物设计参数和组织设计如表1和图3、图4、图5、图6所示，纹样颜色对应的组织分别如图5、图7和图8所示.

表1 布样参数设计Tab.1 The parameters for the jacquard fabric

图3 正交型织物纹样图Fig.3 Jacquard design with orthometric distribution

图4 正交型织物组织分布Fig.4 W eave pattern and the color for orthometric distribution

图5 包围圈型织物纹样图Fig.5 Jacquard design with circular distribution

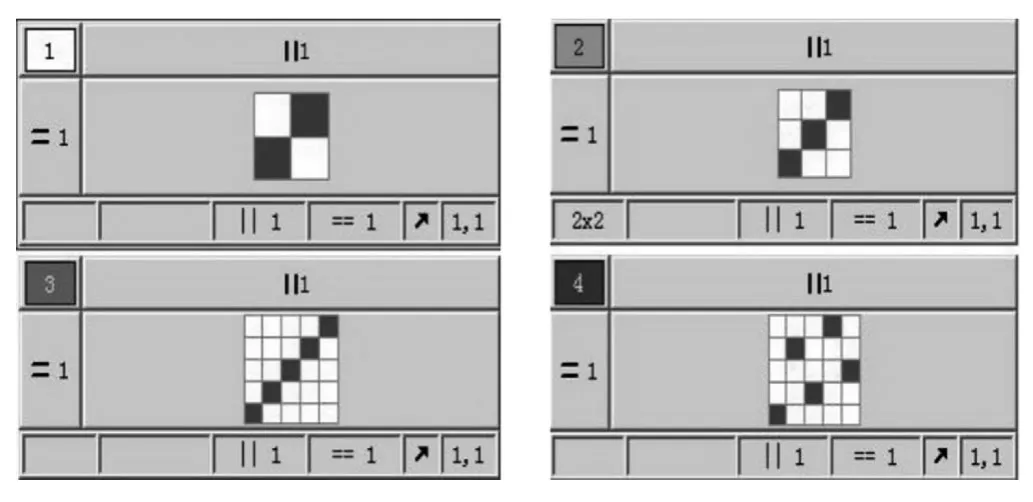
图6 包围圈型织物组织图Fig.6 Weave pattern and the color for circular distribution

根据此设计，在通源电子提花机上织造的织物如图7和图8所示.

图7 正交型组织分布织物图Fig.7 The effects of the woven structures with orthometric distribution

图8 包围圈型组织分布织物图Fig.8 The effects of the woven structures with circular distribution

4.2 织物结构的高精度非破坏测量

在传统的织物结构测量中，切片技术会对织物组织进行挤压和分离，影响测量的准确性和织物结构的完整性.本研究采用Keyence 3D激光共聚焦显微镜对织物表面进行非接触、非破坏性测量织物表面某点的X，Y，Z三维坐标信息，其测量精度达10 nm，远远超过织物几何结构研究的精度要求，测量结果如图9所示.

但是，该仪器仅能获取织物一面的表面效果，在织物屈曲波高研究中，需要同时测量织物正反面纱线交错点同一位置在同一坐标系下的X，Y，Z坐标值，其关键是测量交织点处经纬纱线理论中心Z坐标点的位置.本研究采用Zheng［8］的三维测量与定标技术，在布面插入长度固定的细钢针作为Z基准点定标，也可快速找到正反面同一组织点而方便获得数据.将4只高度已知且相同的小钢针构成的平台插入所要测量的布样内且固定于一矩形区域内，标注好顺序，在钢针标定的矩形区域内对布样进行测量，先测量织物正面的交错点X，Y，Z坐标，然后测量反面.根据钢针的长度，将两次测量的Z坐标值统一在一个坐标系下，这样就得到了织物正反面所有交错点的Z坐标值.

根据此法测量可估算纱线的压扁系数，得到交错纱线截面的理论中心，算出屈曲波高.为了保证在下面的测量中正反面测量的是同一点，用红色笔接触布面染上颜色而形成参照点，如图7和图8所示.由于显微镜测量的精度高、视野小，可用水平移动电动载物台调整测量位置.

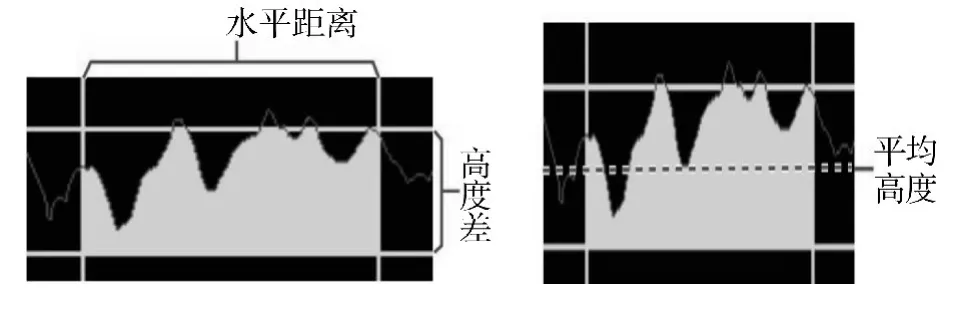
图9 织物表面测量结果示意图Fig.9 Schematic of themeasured result of the fabric surface

4.3 三维测量结果与分析

图10是上述布样中不同交织规律部分的屈曲波高测量结果.

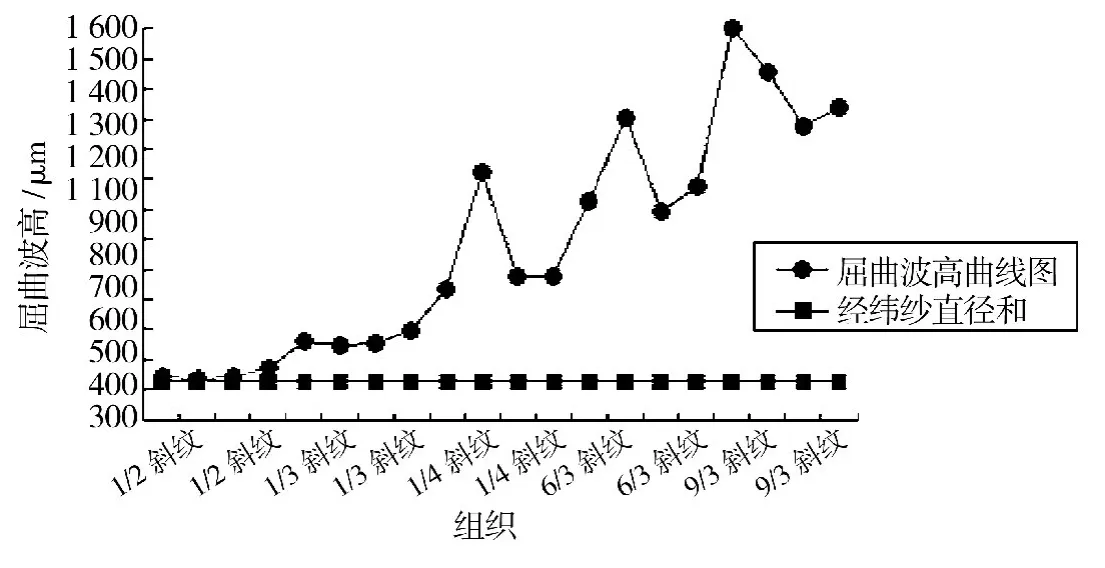
图10 不同结构的屈曲波高曲线图Fig.10 Graph of crimp height of different woven structure

由图10可以看出，对织物组织的正反面均进行比较，在没有考虑机织物的压扁系数且织物组织浮长线较小时，其经纬纱屈曲波高之和与经纬纱直径之和的差异不大，Peirce公式适用.随着织物浮长线的增加，即纱线交织次数的减少，屈曲波高度曲线呈上升趋势.同时，织物经纬纱屈曲波高之和与曲线在经纬纱理论直径之和的差值越来越大，浮长线脱离纱线表面形成凸起，即使考虑纱线的压扁系数，Peirce机织物几何结构模型也不再适用.

5 结论

机织物的几何结构参数的正确计算对织物的风格和性能起着重要的作用，所以有必要对机织物的结构模型进行探讨.本研究从经典教材中的实例检验、织物结构图片的对照以及自行设计织造的织物进行非破坏性测量3个方面验证了机织物Peirce几何结构模型的精度.结果表明，屈曲波高之和与纱线理论直径之和之间不是简单的相等关系，屈曲波高计算的理论值与实际值存在较大差异，需要进一步研究改进.

［1］Peirce F T.The geometry of cloth structure［J］.Journal of Textile Institute，1937，28(3):45-96.

［2］Kemp A.An extension of Peirce’s cloth geometry to the treatment of non-circular threads［J］.Journal of the Textile Institute，1958，49(4):44-48.

［3］Hearle J，Grosberg P，Baker S.Structural Mechanics of Fibers，Yarns and Fabric［M］.New Jersey:John Wiley＆Sons Inc，1969:323-330.

［4］吴汉金，郑佩芳.机织物结构设计原理［M］.上海:同济大学出版社，1990:109-125.

［5］顾平.织物组织与结构学［M］.上海:东华大学出版社，2010:155-170.

［6］蔡陛霞.织物结构与设计［M］.2版.北京:纺织工业出版社，1986:286-289.

［7］郑天勇，黄故.机织物外观分析及计算机三维模拟［J］.纺织学报，2001，22(2):40-43.

［8］Zheng T，Cai Y，Jin S，et al.Study on non-devastating measurement and reconstruction of the woven fabrics’3D geometric structure［J］.Textile Research Journal，2011，81(3):1-12.