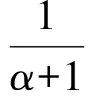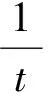差分方程xn+1=f(xn,xn-k)的全局渐近稳定性

姚 勇，孔春莉，李祖雄

(湖北民族学院 理学院，湖北 恩施 445000)

YAO Yong,KONG Chunli,LI Zuxiong

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

差分方程xn+1=f(xn,xn-k)的全局渐近稳定性

姚 勇，孔春莉，李祖雄*

(湖北民族学院 理学院，湖北 恩施 445000)

差分方程；不变区间；全局渐近稳定性

1 引言及预备知识

考虑差分方程:

xn+1=f(xn,xn-k)，n=0,1,…;k=1,2,….

(1)

对于方程(1)在不同条件下的全局吸引性已有许多数学工作者进行了广泛的研究[1-4]，但对于负解的全局吸引性的工作却做得很少.本文运用文献[1]中的某些方法研究方程(1)满足条件：

(H1)f∈C[(-∞,b)×(-∞,b),(-∞,b)]，b≤0是常数；

(H2)f(u,v) 关于u单调增加，关于v单调减少；

为了行文方便，给出一些记号，定义及引理.记I是实数区间，f是Ik+1上的连续函数，记方程:

xn+1=f(xn,xn-1,…，xn-k)，n=0,1,…；k=1,2,….

(2)

定义2 区间J⊆I被称为方程(2)的一个不变区间，如果x-k,…,x-k+1,x0∈J，则xn∈J(n>0)，即当初始条件属于J时，方程(2)的任意解仍在J中.

引理1[5]假设A,B∈R，那么:

|A|+|B|<1

(3)

是差分方程:

xn+1-Axn+Bxn-k=0，n=0,1,2,…;k=1,2,….

(4)

渐近稳定的充分条件；如果还满足下列条件之一：

i)k是奇数且B<0；ii)k是偶数且AB<0.

则方程(3)也是差分方程(4)渐近稳定的必要条件.

引理2[6]考虑差分方程:

xn+1=f(xn,xn-k)，n=0,1,…；k=1,2,….

(5)

设I=[a,b]是一实数区间且假定:f:[a,b]×[a,b]→[a,b]

是一连续函数且满足下列条件：

i)f(u,v)关于u非减，关于v非增；

ii)如果(m,n)∈[a,b]×[a,b]是方程组:

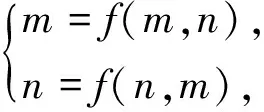
(6)

2 主要结果及证明

定理1 假设条件(H1)～(H3)满足，则方程(1)有唯一的负平衡点.

证明假设x≠y使得:x=f(x,x)，y=f(y,y)

同时成立.不妨设xy同样可证)，则由条件(H1)～(H3)知:x=f(x,x)>f(x,y)，

两边同除以x，有: 1

得出矛盾.所以方程(1)有唯一的负平衡点.

定理2 若方程(1)满足条件(H1)～(H3)，那么下列结论成立：

证明只证1)与3)，其它证明类似.根据条件(H1)～(H3)有:

显然β≤b.方程(1)意味着:xn≤β,n>0.

假设在区间(-∞,b)上满足：

在条件(H4)下，记h(β)是方程f(x,β)=x的唯一解.

定理3 若条件(H1)～(H4)满足，那么存在充分大的正整数N，使得:

h(β)≤xn≤g(β)，n≥N+k+1，

其中g(β)=f(β,h(β)).

为证明这个定理，给出以下引理.

引理3 若条件(H1)～(H4)满足且存在充分大的正整数N使得:xN≥h(β),xN+1≥h(β),…,xN+k≥h(β)，那么xn≥h(β),n≥N.

证明由条件(H1)～(H4)知:xN+k+1=f(xN+k,xN)≥f(xN+k,β)≥f(h(β),β)=h(β).

若对于j≤n都有xN+k+j≥h(β)，则有:xN+k+j+1=f(xN+k+j,xN+j)≥f(h(β),β)=h(β)，所以:xn≥h(β),n≥N.

引理4 若条件(H1),(H2),(H4)满足，且存在正整数N使得:xN≥h(β)，

那么:

xN+i≥h(β),xN+k+i≤g(β),i=1,2,….

证明由条件(H1),(H2),(H4)有:xN+1=f(xN,xN-k)≥f(h(β),β)=h(β)，

xN+k+1=f(xN+k,xN)≤f(β,h(β))=g(β).

由数学归纳法可得:

xN+i≥h(β),xN+k+i≤g(β).

两边同除以h(β)得:

矛盾，所以x>h(β).而:

引理6 若(H1)～(H4)满足，则方程:

f(x,g(β))=x

(7)

综上所述，引理6得证.

证明断定一定存在一个正整数N使得yN≥h(β),否则假设yN

则{yn}严格单调递增.设yn的极限值为I，则有I≤h(β)，

I=f(I,g(β))，

(8)

由引理6和方程(8)有I>h(β)，得出矛盾.因此一定存在一个正整数N使得yN≥h(β).

而由(H2)知:yN+1=f(yN,g(β))>f(h(β),β)=h(β)，

定理3的证明，分三种情况证明.

1) 若存在正整数N使得:xN≥h(β),xN+1≥h(β),…,xN+k≥h(β),

则由引理3，引理4有:h(β)≤xn≤g(β),n≥N+k+1.

2) 若存在正整数N使得:(a):xNh(β);或:(b):xN>h(β),xN+1

由(b)知:xN+1=f(xN,xN-k)>f(h(β),β)=h(β)，所以(b)假设不成立.

现在证明(a)，由引理4知:

xN+i>h(β)≥h(β),i=1,2,…，

又:

xN+k+2=f(xN+k+1,xN+1)≤f(β,h(β))=g(β).

同样由引理4知:

xN+i+k+1≤g(β),i=1,2,….

3)若存在正整数N使得:xnf(xN+k,g(β))=yn

由引理7知总存在正整数N使得:

xn≥h(β),n≥N，

而:

xN+k+1=f(xN+k,xN)≤f(β,h(β)_=g(β)，

综合1)、2)、3)所证知定理5成立.

定理4 若条件(H1)～(H5)满足，系统:

(9)

由定理3和引理2容易得证.

3 应用

考虑方程:

(10)

其中α∈(-∞,-1)∪(-1,0)是一实数，初始条件x-k,x-k+1,…,x0是任意负实数.

当α<-3时，有:

当α∈[-3,-1)时有:

现在考虑方程:

(11)

其中f:I×I→I，其中I=[t(α+t),α+t].

又因为:

(α+t)(α+2t)≤αu+2v≤(α+t)(αt+2)，

又令T(α)=(α+t)(α+2t)，而:

证明取h(β)=(α+t)t,g(β)=α+t,0≤δ≤(α+t)(1-t)，据引理8有:

f(α+t,(α+t)t+δ)≤f(α+t,(α+t)t)=α+t=g(β)，

所以对所有u,v∈I有:h(β)=(α+t)t≤f(u,v)≤g(β)=α+t，即方程(10)中的解{xn}满足:h(β)≤xn≤g(β).

证明设{xn}是方程(10)的任意一个具有初值x-k,x-k+1,…,x0∈I的解.对u,v∈I满足式(11)，则f:I×I是一连续函数，由引理8和定理6知：f满足(H1)～(H5)，现在只要证满足下列方程组的解是m=n，令:

则有:

(m-n)(m+n-α+1)=0，

若m+n-α+1=0，则有:m+n=α-1，因而有:n2-(α-1)n-(α-1)=0，

也就是:

由此得:

即:

得出矛盾.

同样得出矛盾.所以:m+n-α+1≠0，

[1]Fan Y H,Wang L L,Li W T.Global behavior of a higher order nonlinear diffrernce equation[J].J Math Anal Appl,2004,299:113-126.

[4]Kocic V L,Ladas G.Global behavior of nonlinear difference equations of higher orderwith application[M].Dordrecht：Kluwer Academic,1993.

责任编辑：时凌

GloballyAsymptoticalStabilityoftheDifferencexn+1=f(xn,xn-k)

difference equation；invariant interval；globally asymptotical stability

2014-09-22.

教育部科学技术研究重点项目(212111);湖北民族学院大学生创新项目(2013Z017).

姚勇(1989- )，男(土家族)，硕士生，主要从事微分方程理论及其应用的研究.*

：李祖雄(1972- )，男(土家族)，博士，副教授，主要从事微分方程理论及其应用研究.

O175.7

A

1008-8423(2014)04-0393-05

YAO Yong,KONG Chunli,LI Zuxiong

(School of Science,Hubei University for Nationalities,Enshi 445000,China)