椭球膨胀法在高原长距离工程中的应用

张 辛，姜本海，李志鹏，罗洪波

(长江勘测规划设计研究院，湖北 武汉 430010)

椭球膨胀法在高原长距离工程中的应用

张 辛，姜本海，李志鹏，罗洪波

(长江勘测规划设计研究院，湖北 武汉 430010)

对5种椭球膨胀方法进行系统的理论推导与分析，并在云南滇中引水这一典型的高原长距离工程中应用。研究获取椭球长半轴变化量、基准点大地坐标变化量、测区端点高斯坐标变化量与长度变形值等测算数据，并分析各种椭球膨胀方法数据结果的差异性与合理性。结果表明，平面解析法与广义微分法更适合作为高原长距离工程的椭球膨胀方法。

椭球膨胀；高原；独立坐标系统；平面解析法；广义微分法

对于高原长距离工程，存在测区远离中央子午线与平均高程较大的问题，若使用国家坐标系统会导致测距边的长度变形扩大，难以满足工程的精度要求，因而需要建立工程独立坐标系统[1-2]。独立坐标系统建立时，常使用椭球变换的方式缩小投影变形[3-5]。椭球变换方法包括椭球膨胀法、椭球平移法和椭球变形法等，其中椭球膨胀法在工程实践中应用广泛[6]。

1 椭球膨胀方法理论

椭球膨胀法的基本原理：保持椭球中心与椭球扁率不变，使椭球膨胀放大到所需的投影面高度。如图1 所示，P0为地面上的基准点，其在基础椭球E1上的对应点为P1，E1沿P0的法线方向P0P1膨胀Δh到所定义的投影面Fh，形成膨胀后的椭球E2，E2上的对应点为P2；其中Δh为P1到P2点的距离，即Fh为投影面在基础椭球E1上的大地高。椭球膨胀前后，椭球的长半轴发生变化，而针对其变化量存在多种计算方式[7-10]。

图1 椭球膨胀示意图

1.1 直接法

直接法是直接将投影面大地高定为椭球长半轴的变化量，即Δa=Δh。

1.2 平均曲率半径法

该方法近似认为椭球膨胀过程是沿着P1点处的平均曲率半径的方向。

(1)

式中：R1，R2分别为基准点在基础椭球与膨胀椭球上的平均曲率半径；M，N为基础椭球的子午圈曲率半径和卯酉圈曲率半径；a1，a2分别为基础椭球和膨胀椭球的长半轴；e为椭圆的第一偏心率；B1，B2分别是基准点在基础椭球与膨胀椭球的大地纬度。由式(1)推得

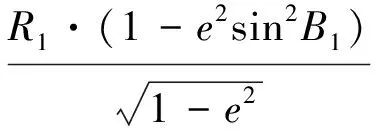
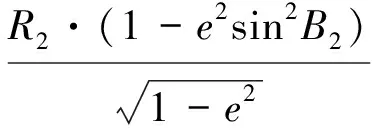
(2)

由于B1≈B2，因此可求得长半轴的变化量为

(3)

1.3 卯酉曲率半径法

由于基础椭球是沿着法线P0P1的方向进行膨胀；假设膨胀后的椭球E2在P2处的法线与P0P1重合，则投影面的大地高等于卯酉圈曲率半径N的变化量，即ΔN=Δh，再由

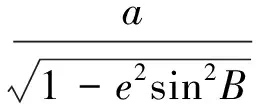
(4)

得出

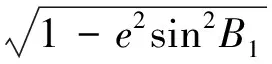
(5)

同样由B1≈B2，可以得到长半轴的变化量为

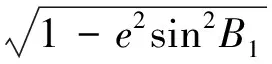
(6)

1.4 平面解析法

上述几种方法均存在近似的推导过程，如卯酉圈曲率半径法是在假设椭球膨胀前后的法线重合，并且有B1≈B2时实现。但由于椭球面具有各向异性，所以椭球膨胀后法线的方向可能变化，并且基准点的纬度也可能不同。因此，需要用更严密的解析法推导椭球长半轴的变化量。

如图2所示，在子午平面直角坐标系中，基础椭球在P1处的法线方向仍是P1P2，并延长交椭球短半轴于n1点，即P1n1为P1点在基础椭球E1上的卯酉圈曲率半径；而膨胀椭球E2在P2点的法线方向为P2n2，即P2n2为P2点在膨胀椭球E2上的卯酉圈曲率半径。在此平面坐标系统中，P1点的坐标(X1,Y1)与P2点的坐标(X2,Y2)分别为

X1=P1n1·cos (B1)=N1·cos (B1)，

Y1=P1Q1·sin (B1)=N1·(1-e2)·sin (B1);

(7)

X2=P2n2·cos (B2)=N2·cos (B2)，

Y2=P2Q2·sin (B2)=N2·(1-e2)·sin (B2).

(8)

再由P1P2=Δh，也可推得P2点的坐标为

X2=P2n1·cos (B1)=(N1+Δh)·cos (B1)，

Y2=P2Q1·sin (B1)=N1·(1-e2)·

sin (B1)+Δh·sin (B1).

(9)

由式(8)、式(9)得

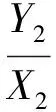
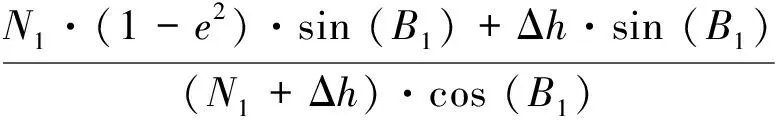
(10)

由式(10)变换，求得tan (B2)表达式为

(11)

由式(11)可知，膨胀椭球的大地纬度B2总是大于等于B1；并可由此式求得B2。再由式(8)与式(9)中X2的表达式，可得N2的表达式为

(12)

综合式(5)中a2的表达式，及式(11)与式(12)，可得到膨胀椭球E2的长半轴a2与Δh的关系式。

图2 椭球膨胀平面解析法

1.5 广义微分法

该方法是利用广义大地坐标微分公式确定椭球长半轴变化量。对于广义椭球的变换模型，广义大地坐标微分公式为

(13)

代入不同的平移参数(dX0,dY0,dZ0)、旋转参数(εX,εY,εZ)、椭球几何要素(da,d∂)和尺度因子Δm，可以计算得出椭球变换后的大地坐标变化量。由于椭球膨胀法不改变椭球的定位、定向、尺度和扁率，因此微分公式中包含空间坐标转换的8个参数项全部可以忽略，仅保留椭球长半轴的变化量，化简后可得到P点从基础椭球E1的大地坐标(B1,L1,H1)到膨胀椭球E2的变化量为

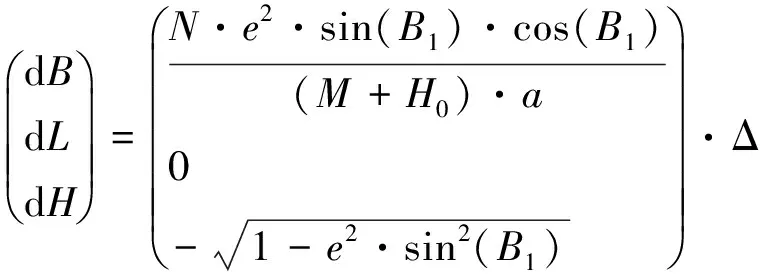
(14)

式中：M为子午圈曲率半径。在椭球膨胀过程中，投影面与E2椭球面越接近，吻合程度越好，若要投影面与E2椭球面重合，则有

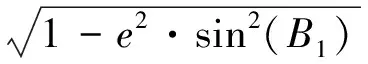
(15)

进而得到长半轴的变化量为

(16)

2 工程应用实例分析

本文使用云南滇中引水工程的分段干线数据对多种椭球膨胀方法分别进行分析。滇中引水工程全长共约850 km ，其中东西跨度约400 km ，南北跨度约545 km ，引水线路从海拔2 064 m至海拔1 401 m,是典型的高原长距离大型线性工程。

2.1 国家3°带测区分析

滇中引水工程干渠线路从东经99°～103°，跨越了两个国家3°投影带，本文只选取分段的102°中央子午线区域进行分析。该测段从东经100°30′延伸至103°29′，基本在中央子午线两侧平均分布。因此，在进行椭球膨胀时，选择的膨胀基准点为经度L0=102°处。此外，该测段的平均正常高为1800 m，区域高程异常为29.933 m，所以得到投影面高程Δh=1 829.933 m。再使用上述介绍的椭球膨胀方法分别计算椭球长半轴的变化量，如表1所示。其中，平均曲率半径法的变化量最大，卯酉曲率半径法变化量最小，而居中的3个变化量中，平面解析法与广义微分法的变化量极为接近，仅有1.7×10-6m的差值。

由椭球长半轴的变化量能够获取膨胀后的椭球参数，从而获取新椭球上各点的大地坐标。此处针对基准点，分别求取经度、纬度与高程的变化量，见表2。其中，各种方法的经度变化均为零，纬度变化均是正值，这与广义微分法获取的式(14)吻合，并且，也能看到膨胀前后的基准点纬度差异较为明显，平均曲率半径法与卯酉曲率半径法忽略了这种纬度差，模型不严密。

此外，不同方法的高程变化差异较大，这反映采用不同方法进行膨胀后，投影面与膨胀椭球E2的吻合度有所差异；高程变化的数值越小，吻合程度越好。因此，无高程差异的平面解析法是吻合程度最好的，其次是广义微分法，有2×10-6m的微小差值；而平均曲率半径法与卯酉曲率半径法的吻合效果较差，高程吻合度均不如直接法。

从上述分析可知，使用不同方法对滇中引水测区进行椭球膨胀，会造成显著的椭球长半轴差值与基准点高程变化差值。由于工程要求进行高斯投影变换，则投影变换后的坐标差异仍有待探求。本文对测区的西端点(L=100°30′)与东端点(L=103°29′)，使用不同的椭球膨胀方法，分别进行高斯投影变换，并统计端点的平面距离，再与原始椭球的坐标与距离求差值。如表3所示，分别列出两端点的ΔX,ΔY及平面距离差。其中，使用平均曲率半径法获取的高斯投影坐标值最大，相应的端点平面距离最长；使用卯酉曲率半径法获取的坐标值最小，端点平面距离也最小；端点坐标差值最大达2.236 m，平面距离差值最大为0.310 m，差异较为明显。由于滇中引水工程线路较长，计划使用1°的高斯投影方式控制投影变形；因此，本文也继续使用1°带测区进行椭球膨胀方法的比较分析。

2.2 国家1°带测区分析

为了与上述的3°带测区结果形成对比，本文在1°带测区中也选择102°中央子午线区域进行分析。该测段从西端点(L=101°30′)延伸至东端点(L=102°30′)，均匀分布在中央子午线两侧。因此，选择的椭球膨胀基准点仍为经度L0=102°处；投影面高程仍是Δh=1 829.933 m。使用不同的椭球膨胀方法获取的长半轴变化量与基准点大地坐标变化量与3°带测区相同。因此，只在1°带测区内对端点进行高斯投影变换，统计端点的平面距离，并仍与原始椭球的坐标及距离求差值，具体数据如表4所示。

其中，端点坐标差值最大仍能达2.213 m，而平面距离差值最大为0.060 m。可见，即使在1°带测区内，不同膨胀方法带来的高斯坐标差异仍较大。两端点的平面距离差值虽有大幅下降，但这是基于测区从3°范围减小为1°范围而引起的。为了更准确地分析不同椭球膨胀方法的差异，本研究进一步进行单位长度的变形分析。如表5所示，是针对各种椭球膨胀方法分别计算两端点的高斯投影变形量与高程归化变形量[7]。由表中数据分析可知，各膨胀方法的高斯投影变形相同，这是由于各点的Y值变化很小(见表4)，高斯变形量变化甚微。各方法带来的高程变形差异较大，最大差值可达0.08 cm/km,这种变形差异正是来自于投影面与膨胀椭球的吻合度差异，如前面针对表2数据的分析，吻合度最好的平面解析法与广义微分法计算的高程归化变形值一致。

表1 椭球长半轴的变化量 m

表2 膨胀椭球上基准点大地坐标变化量

表3 椭球膨胀后3°带高斯投影比较 m

表4 椭球膨胀后1°带高斯投影比较 m

表5 椭球膨胀后1°带长度变形 cm/km

3 椭球膨胀方法的适用性分析

综上分析，在滇中引水这一典型的高原长距离工程中，使用不同的椭球膨胀方法构建坐标系统后，计算得到的点位坐标与高程有较大差异。因此选择合适的椭球膨胀方法对工程坐标系统的建立尤为重要。

直接法是简化的模型方法，其理论基础不完善，不推荐在大型工程中应用。

平均曲率半径法将椭球膨胀方向近似为椭球的平均曲率方向，并忽略膨胀前后基准点的纬度差异。在滇中引水工程计算时，其点位坐标、高程值与其它模型方法差异较大，应避免在长距离工程中使用。但该方法在局部区域能一定程度地削弱椭球面不平行造成的误差，可考虑在小范围工程中使用[8]。

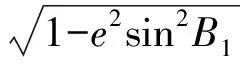
4 结束语

在各种方法中，理论最严密的是平面解析法与广义微分法。前者是利用平面解析几何的方式推导详细的膨胀椭球长半轴计算公式，后者是基于广义大地坐标微分公式确定椭球长半轴变化量；两种方法在滇中引水工程计算中的结果互为印证，是本工程推荐使用的椭球膨胀方法。但这两种方法中，平面解析法模型构建复杂，使用不太便利；而广义微分法在投影面与椭球的吻合度上有微小误差(如表2所示)，均有进一步改进的空间。

[1]施一民.现代大地控制测量[M].北京：测绘出版社,2003.

[2]L SANCHEZ, C BRUNINI.Achievements and Challenges of SIRGAS, Geodetic Reference Frames[C].International Association of Geodesy Symposia, Munich, Germany, 2006.

[3]施一民，张文卿.区域椭球元素的最佳确定[J].测绘工程, 2000, 9(3):27-40.

[4]陈引川, 王洪伟, 张立朝.利用坐标反算的投影网格算法[J] 测绘科学技术学报, 2010,27(2):146-148,152.

[5]杨爱明,严建国,杨成宏,等.南水北调中线工程施工测量控制网系统研究[J].人民长江,2010,41(19):30-33.

[6]李世安，刘经南，施闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报：信息科学版，2005,30(10) :888-891.

[7]于亚杰, 赵英杰, 张月华.基于椭球膨胀法实现独立坐标系统的建立[J].测绘通报, 2011(12):33-36.

[8]王磊, 郭际明, 申丽丽, 等.顾及椭球面不平行的椭球膨胀法在高程投影面变换中的应用[J].武汉大学学报：信息科学版,2013,38(6):725-733.

[9]余代俊.试论选择地方参考椭球体长半径的合理公式[J].测绘科学, 2005,30(5):36-38.

[10]尹伟言，赵鑫.区域性椭球元素确定方法的比较[J].测绘工程, 2013,22(4):26-29.

[责任编辑：张德福]

Ellipsoid expansion methods in highland long-distance project

ZHANG Xin，JIANG Ben-hai，LI Zhi-peng，LUO Hong-bo

(Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430010，China)

Five kinds of ellipsoid expansion methods are systematically analyzed and applied to the water diversion project in Central Yunnan, as the typical high altitude long-distance project.Firstly, this research obtains the semi-major axis of ellipsoid, geodetic coordinate variation of reference points, gauss coordinate variation of endpoints, and length variation.Then, the difference and rationality of all the ellipsoid expansion methods are analyzed.The results indicate the plane analytic method and generalized differential method are more suitable as the ellipsoid expansion methods of high altitude long-distance project.

ellipsoid expansion; highlands; independent coordinate system; plane analytic method; generalized differential method

2014-02-24

湖北省博士后创新岗位基金资助项目

张 辛(1983-)，男，博士后，工程师.

P221

：A

：1006-7949(2014)09-0040-05