顾及系数矩阵常数列的总体最小二乘迭代解法

汪奇生，杨德宏

(昆明理工大学 国土资源工程学院, 云南 昆明 650093)

顾及系数矩阵常数列的总体最小二乘迭代解法

汪奇生，杨德宏

(昆明理工大学 国土资源工程学院, 云南 昆明 650093)

介绍总体最小二乘的奇异值分解法(SVD)和混合总体最小二乘法(LS -TLS)，基于间接平差原理推导一种总体最小二乘迭代解法，可以用来解决系数矩阵含常数列的总体最小二乘平差问题。最后分别对系数矩阵不含常数列和系数矩阵含常数列的算例进行验证，得到的结果与采用奇异值分解法和混合总体最小二乘法计算的结果相同，表明算法的有效性。

总体最小二乘；间接平差；迭代解法；混合总体最小二乘；奇异值分解

在测量数据处理中，对于系数矩阵含有误差的平差问题，采用总体最小二乘法[1]要比采用最小二乘法在理论上更加严密。近年来，总体最小二乘得到了测量学者们的广泛关注，一些针对测量数据处理的迭代算法相继被提出[2-6]。同时，总体最小二乘也被用来解决具体的测量问题[7-10]。但在实际的测量数据处理中，系数矩阵有可能不是所有元素都含有误差，而一些常规的迭代算法与奇异值分解法(SVD)一样都无法顾及系数矩阵的常数列，而是对系数矩阵所有元素都进行了改正，这是不合理的。因此，混合总体最小二乘法[7-9]被用来解决系数矩阵含常数列的总体最小二乘问题，但混合总体最小二乘解算较为复杂。鉴于此，本文基于间接平差原理推导了一种总体最小二乘迭代算法。该算法充分考虑了间接平差的优点，推导过程简单且能顾及系数矩阵中的常数列，使用方便。最后通过线性拟合和坐标转换的算例验证了算法的合理性和有效性。

1 奇异值分解法与混合总体最小二乘法

1.1 奇异值分解法(SVD)

总体最小二乘的平差模型为

(1)

式中，V,EA分别表示观测向量L和系数矩阵A的误差，根据总体最小二乘原理，对参数估计的准则为

VTV+vec(EA)Tvec(EA)=min.

(2)

式中，vec(·)表示矩阵的拉直运算。一般采用奇异值分解法[1-3]来求取参数的总体最小二乘解。将式(1)可变换为

(3)

(4)

其中：

为求得参数的估值使式(2)达到最小，可将式(3)改为

(5)

则可得参数的估值

(6)

其残差矩阵为

(7)

进一步可计算单位权中误差以及参数的协方差

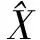
(8)

1.2 混合总体最小二乘法(LS -TLS)

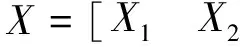
(9)

式中:A1为系数矩阵的常数列，A2为除常数列后的数据列。混合总体最小二乘的约束条件为

(10)

(11)

为求得参数的估值使式(10)达到最小，可将式(3)改为

(12)

由式(11)、式(12)即可得

R11X1+R12X2=R1L，

R22X2=R2L.

(13)

2 算法推导

将式(1)表示成V的函数为

L.

(14)

vec(ΔeA)=ΔvA.

(15)

式中,vec表示向量拉直运算，由文献可知

vec(ABC)=(CT⊗A)vec(B).

(16)

化简整理后可得

(17)

式中，⊗为矩阵的可内克积。根据总体最小二乘原理，求解的参数需要满足如下极值条件：

VTV+(VA)TVA=min.

(18)

则可将式(17)写成间接平差形式

(19)

根据间接平差原理，参数的求解为

(20)

单位权中误差评定公式为

(21)

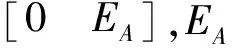
根据前述推导，总体最小二乘迭代解法的具体步骤如下：

1)按总体最小二乘原理计算参数的初值X0。

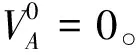
4)重复3)，直到两次计算的参数之差小于给定的迭代限差，则停止迭代。

5)输出参数值，计算单位权中误差。

3 算例分析

3.1 线性拟合

方案1：直接采用奇异值分解法求得的线性回归方程为y=6.74-0.99x。

方案2：根据文献[2]将数据中心化后，再采用奇异值分解法求得的线性回归方程为y=6-x。

方案3：直接采用混合总体最小二乘法求得的线性回归参数y=6-x。

方案4：直接采用本文推导的迭代算法求得的线性回归方程为y=6-x。

从以上4种方案中可以看出，方案1直接采用奇异值分解法而没有顾及系数矩阵常数列得到的结果不合理，方案2将数据中心化后，系数矩阵变为一列元素且不含常数列，再采用奇异值分解法求得的结果与方案3中直接采用混合总体最小二乘法求得的结果一致，是正确合理的。而方案4中直接采用本文的迭代算法求得的结果与方案2、方案3一致，故本文算法是合理有效的。

3.2 坐标转换

为进一步验证本文算法的正确性，选取文献[11]例7～14的数据，用5个拥有WGS-84和北京54坐标的公共点来求取坐标转换参数。根据坐标转换的平差模型可知，其系数矩阵含有3列常数列，分别采用最小二乘法(LS)、混合总体最小二乘法(LS -TLS)、本文的总体最小二乘算法(TLS)来计算坐标转换参数，计算结果如表1所示，单位权中误差评定如表2所示。

表1 不同方法求得的坐标转换参数

表2 不同方法的单位权中误差评定结果 m

从表1的不同方法求得的坐标转换参数计算结果可以看出，采用本文的迭代算法求得的转换参数与采用混合总体最小二乘法求得的结果一致，这是因为本文算法可以顾及系数矩阵的常数列且对其不进行改正，而混合总体最小二乘法正是只改正系数矩阵含误差的那部分。这也可以从单位权中误差的评定结果中看出，采用本文的迭代算法计算的单位权中误差与采用混合总体最小二乘法计算的结果一致，且小于采用最小二乘计算的结果。这也说明采用总体最小二乘求取坐标转换参数要比采用最小二乘的精度高，故本文给出的算法较为合理。

4 结束语

基于间接平差原理，推导了一种总体最小二乘迭代算法。该算法推导过程简捷易懂，迭代格式简单且易于编程实现。同时，该算法可以顾及系数矩阵的常数列，这弥补了总体最小二乘的奇异值分解法和常规的总体最小二乘迭代算法的不足。通过最后的算例验证了本文算法的合理性。

[1]GOLUB G H，VAN L C F. An Analysis of the Total Least Squares Problem[J].SIAM J Numer. Anal，1980，17:883-893．

[2]邱卫宁，陶本藻，姚宜斌，等.测量数据处理理论与方法[M].武汉: 武汉大学出版社, 2008．

[3] 鲁铁定,周世健.总体最小二乘的迭代解法[J].武汉大学学报：信息科学版，2010,35(11) :1351-1354.

[4] 许超钤，姚宜斌，张豹,等.基于整体最小二乘的参数估计新方法及精度评定[J].测绘通报，2011(10):1-4.

[5] 孔建，姚宜斌，吴寒．整体最小二乘的迭代解法[J]．武汉大学学报:信息科学版，2010，35(6):711-714．

[6] 邱卫宁,齐公玉,田丰瑞. 整体最小二乘求解线性模型的改进算法[J].武汉大学学报：信息科学版，2010，35(6):708-710.

[7]张海华，刘春.顾及粗差的混合最小二乘平差实验分析[J].现代测绘，2010，33(5):8-11.

[8]陈义，陆珏，郑波．总体最小二乘方法在空间后方交会中的应用[J].武汉大学学报：信息科学版， 2008,33(12):1271-1274.

[9]陆珏，陈义，郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学，2008,28(5):77-81.

[10]刘运明，邹积亭，边春雷.基于整体最小二乘的盾构环中心拟合方法[J].测绘通报，2010(Z):174-176.

[11]袁豹,岳东杰.关于总体最小二乘方法适应性实验研究[J].测绘工程，2012，21(6):22-26.

[12] 武汉大学测量平差学科组编.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003.

[责任编辑：刘文霞]

Iterative algorithm of total least squares considering the constant sequence of coefficient matrix

WANG Qi-sheng，YANG De-hong

(School of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093，China)

It briefly introduces a total least squares singular value decomposition (SVD) and mixed total least squares (LS-TLS). An iterative algorithm for total least squares is derived based on a principle of indirect adjustment, which can be used to solve the adjustment problems of total least squares for coefficient matrix containing constant sequence. Finally, numerical examples of the coefficient matrix with out constant sequence and with constant series are analyzed respectively. The results are the same used by the singular value decomposition method and the mixed total least squares and shows the effectiveness of the algorithm.

total least squares; indirect adjustment; iteration algorithm; mixed total least squares (LS-TLS); singular value decomposition (SVD)

2013-07-15

汪奇生(1989-)，男，硕士研究生.

P207

：A

：1006-7949(2014)07-0038-03